E7 (математика) - E7 (mathematics)
| Алгебраическая структура → Теория групп Теория групп |
|---|
 |
Бесконечномерная группа Ли
|
| Группы Ли |
|---|
 |
|
В математика, E7 это имя нескольких тесно связанных Группы Ли, линейный алгебраические группы или их Алгебры Ли е7, все они имеют размер 133; то же обозначение E7 используется для соответствующего корневая решетка, который имеет ранг 7. Обозначение E7 исходит из Классификация Картана – Киллинга комплекса простые алгебры Ли, которые распадаются на четыре бесконечные серии, обозначенные Aп, Bп, Сп, Dп, и пять исключительных случаев маркированный E6, E7, E8, F4, и г2. E7 алгебра, таким образом, является одним из пяти исключительных случаев.
Фундаментальная группа (присоединенной) комплексной формы, компактной вещественной формы или любой алгебраической версии E7 это циклическая группа Z/2Z, и это группа внешних автоморфизмов это тривиальная группа. Размер его фундаментальное представление 56 лет.
Реальные и сложные формы
Существует единственная комплексная алгебра Ли типа E7, соответствующая комплексной группе комплексной размерности 133. Комплексно присоединенная группа Ли E7 из сложное измерение 133 можно рассматривать как простую действительную группу Ли действительной размерности 266. Она имеет фундаментальную группу Z/2Z, имеет максимальное компактный подгруппу компактную форму (см. ниже) группы E7, и имеет группу внешних автоморфизмов порядка 2, порожденную комплексным сопряжением.
Как и комплексная группа Ли типа E7, есть четыре действительные формы алгебры Ли и, соответственно, четыре действительные формы группы с тривиальным центром (все из которых имеют алгебраическое двойное покрытие, а три из которых имеют дополнительные неалгебраические покрытия, дающие дополнительные действительные формы), все реальной размерности 133, а именно:
- Компактная форма (которая обычно подразумевается, если не дается никакой другой информации), которая имеет фундаментальную группу Z/2Z и имеет тривиальную группу внешних автоморфизмов.
- Разделенная форма, EV (или E7(7)), которая имеет максимальную компактную подгруппу SU (8) / {± 1}, фундаментальную циклическую группу порядка 4 и группу внешних автоморфизмов порядка 2.
- EVI (или E7(-5)), которая имеет максимальную компактную подгруппу SU (2) · SO (12) / (центр), фундаментальную нециклическую группу порядка 4 и тривиальную группу внешних автоморфизмов.
- EVII (или E7(-25)), имеющую максимальную компактную подгруппу SO (2) · E6/ (центр), бесконечная циклическая фундаментальная группа и группа внешних автоморфизмов порядка 2.
Полный список действительных форм простых алгебр Ли см. список простых групп Ли.
Компактная вещественная форма E7 это группа изометрии 64-мерного исключительного компакта Риманово симметрическое пространство EVI (у Картана классификация ). Он неофициально известен как "кватероктонионная проективная плоскость "потому что его можно построить с помощью алгебры, которая является тензорным произведением кватернионы и октонионы, и также известен как Проективная плоскость Розенфельда, хотя и не подчиняется обычным аксиомам проективной плоскости. Систематически это можно увидеть, используя конструкцию, известную как магический квадрат, из-за Ганс Фройденталь и Жак Титс.
В Конструкция Титса – Кехера производит формы E7 Алгебра Ли из Алгебры Альберта, 27-мерное исключительное Йордановы алгебры.
E7 как алгебраическая группа
С помощью Основа Шевалле для алгебры Ли можно определить E7 как линейная алгебраическая группа над целыми числами и, следовательно, над любым коммутативным кольцом и, в частности, над любым полем: это определяет так называемую расщепляемую (иногда также известную как «раскрученную») присоединенную форму E7. Над алгебраически замкнутым полем это и его двойное покрытие являются единственными формами; однако, помимо других областей, часто существует множество других форм или «поворотов» E7, которые классифицируются в общих рамках Когомологии Галуа (через идеальное поле k) по множеству ЧАС1(k, Aut (E7)) который, поскольку диаграмма Дынкина E7 (увидеть ниже ) не имеет автоморфизмов, совпадает с ЧАС1(k, E7, ad).[1]
Над полем действительных чисел действительная составляющая тождества этих алгебраически скрученных форм E7 совпадают с тремя упомянутыми действительными группами Ли над, но с тонкостью, касающейся фундаментальной группы: все присоединенные формы E7 иметь фундаментальную группу Z/2Z в смысле алгебраической геометрии, что означает, что они допускают ровно одно двойное покрытие; дальнейшие некомпактные вещественные групповые формы Ли E7 поэтому не алгебраичны и не допускают точных конечномерных представлений.
Над конечными полями Теорема Лэнга – Стейнберга. подразумевает, что ЧАС1(k, E7) = 0, что означает, что E7 не имеет закрученных форм: см. ниже.
Алгебра
Диаграмма Дынкина
В Диаграмма Дынкина для E7 дан кем-то ![]() .
.
Корневая система

Диаграмма Кокстера – Дынкина:
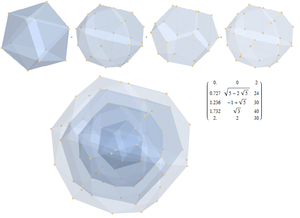
u = (1, φ, 0, -1, φ, 0,0)
v = (φ, 0, 1, φ, 0, -1,0)
w = (0, 1, φ, 0, -1, φ,0)
Прогнозируемый 231 многогранник вершины сортируются и подсчитываются по их трехмерным нормам, создавая все более прозрачные оболочки каждого набора установленных норм. Эти шоу:
1) 2 точки в начале координат
2) 2 икосаэдра
3) 1 икосадодекаэдр
4) 2 додекаэдра
5) 1 икосадодекаэдр
всего 126 вершин.
Несмотря на то, что корни охватывают 7-мерное пространство, более симметрично и удобно представлять их как векторы, лежащие в 7-мерном подпространстве 8-мерного векторного пространства.
Корни представляют собой все 8 × 7 перестановок (1, −1,0,0,0,0,0,0) и все перестановки (½, ½, ½, ½, −½, −½, −½, −½)
Обратите внимание, что 7-мерное подпространство - это подпространство, в котором сумма всех восьми координат равна нулю. Всего 126 корней.
В простые корни находятся
- (0,−1,1,0,0,0,0,0)
- (0,0,−1,1,0,0,0,0)
- (0,0,0,−1,1,0,0,0)
- (0,0,0,0,−1,1,0,0)
- (0,0,0,0,0,−1,1,0)
- (0,0,0,0,0,0,−1,1)
- (½,½,½,½,−½,−½,−½,−½)
Они перечислены так, что их соответствующие узлы в Диаграмма Дынкина упорядочиваются слева направо (на схеме, изображенной выше) боковым узлом последним.
Альтернативное описание
Альтернативное (7-мерное) описание корневой системы, которое полезно при рассмотрении E7 × СУ (2) как подгруппа E8, это следующее:
Все перестановки (± 1, ± 1,0,0,0,0,0) с сохранением нуля в последней записи, все следующие корни с четным числом + ½
и два следующих корня
Таким образом, генераторы состоят из 66-мерного так(12) подалгебра, а также 64 генератора, которые преобразуются как два самосопряженных Спиноры Вейля из вращение(12) противоположной киральности, и их генератор киральности, и два других генератора киральностей .
Учитывая E7 Матрица Картана (ниже) и Диаграмма Дынкина порядок узлов: ![]()
- один выбор простые корни задается строками следующей матрицы:
Группа Вейля
В Группа Вейля из E7 имеет порядок 2903040: это прямое произведение циклической группы порядка 2 и единственной простая группа заказа 1451520 (который можно обозначить как ПСП6(2) или PSΩ7(2)).[2]
Матрица Картана

Важные подалгебры и представления
E7 имеет подалгебру SU (8), что очевидно из того, что в 8-мерном описании корневой системы первая группа корней идентична корням SU (8) (с тем же Подалгебра Картана как в E7).
Помимо 133-мерного присоединенного представления существует 56-мерное "векторное" представление, можно найти в E8 присоединенное представительство.
Характеры конечномерных представлений вещественных и комплексных алгебр Ли и групп Ли задаются Формула характера Вейля. Размерности наименьших неприводимых представлений равны (последовательность A121736 в OEIS ):
- 1, 56, 133, 912, 1463, 1539, 6480, 7371, 8645, 24320, 27664, 40755, 51072, 86184, 150822, 152152, 238602, 253935, 293930, 320112, 362880, 365750, 573440, 617253, 861840, 885248, 915705, 980343, 2273920, 2282280, 2785552, 3424256, 3635840...
Подчеркнутые члены в приведенной выше последовательности являются размерностями тех неприводимых представлений, которыми обладает присоединенная форма E7 (эквивалентно, те, веса которых принадлежат решетке корней E7), а полная последовательность дает размерности неприводимых представлений односвязной формы E7. Существуют неизоморфные неприводимые представления размерностей 1903725824, 16349520330 и т. Д.
В фундаментальные представления имеют размеры 133, 8645, 365750, 27664, 1539, 56 и 912 (соответствуют семи узлам в Диаграмма Дынкина в порядке, выбранном для Матрица Картана выше, то есть узлы считываются первыми в цепочке из шести узлов, причем последний узел подключается к третьему).
E7 Полиномиальные инварианты
E7 группа автоморфизмов следующей пары многочленов от 56 некоммутативных переменных. Мы разделим переменные на две группы по 28, (п, п) и (q, Q) где п и q являются действительными переменными и п и Q 3 × 3 октонион эрмитовы матрицы. Тогда первый инвариант - это симплектический инвариант Sp (56, р):
Второй более сложный инвариант - это симметричный полином четвертой степени:
куда а оператор двоичного круга определяется как .
Альтернативный полиномиальный инвариант четвертой степени, построенный Картаном, использует две антисимметричные матрицы 8x8, каждая с 28 компонентами.
Группы Шевалле типа E7
Точки над конечное поле с участием q элементы (расщепленной) алгебраической группы E7 (увидеть над ), будь то сопряженной (бесцентровой) или односвязной формы (ее алгебраическое универсальное покрытие), дают конечную Группа Шевалле. Это тесно связано с группой, написанной E7(q), однако в этих обозначениях есть двусмысленность, которая может означать несколько вещей:
- конечная группа, состоящая из точек над Fq односвязной формы E7 (для наглядности можно написать E7, сбн(q) и известна как «универсальная» группа Шевалле типа E7 над Fq),
- (редко) конечная группа, состоящая из точек над Fq присоединенной формы E7 (для наглядности можно написать E7, ad(q) и известна как «присоединенная» группа Шевалле типа E7 над Fq), или
- конечная группа, которая является образом естественного отображения от первого ко второму: это то, что мы будем обозначать E7(q) в дальнейшем, как это обычно бывает в текстах, посвященных конечным группам.
С точки зрения конечных групп, отношения между этими тремя группами, которые вполне аналогичны отношениям между SL (п, q), PGL (п, q) и PSL (п, q), можно резюмировать следующим образом: E7(q) прост для любого q, E7, сбн(q) это его Обложка Schur, а буква E7, ad(q) лежит в своей группе автоморфизмов; кроме того, когда q является степенью двойки, все три совпадают, в противном случае (когда q нечетно) множитель Шура E7(q) равно 2 и E7(q) имеет индекс 2 в E7, ad(q), что объясняет, почему E7, сбн(q) и E7, ad(q) часто записываются как 2 · E7(q) и E7(q) · 2. С точки зрения алгебраической группы, для E7(q) для обозначения конечной простой группы, поскольку последняя не является естественным образом множеством точек алгебраической группы над Fq в отличие от E7, сбн(q) и E7, ad(q).
Как упоминалось выше, E7(q) прост для любого q,[3][4] и он составляет одно из бесконечных семейств, адресованных классификация конечных простых групп. Его количество элементов определяется формулой (последовательность A008870 в OEIS ):
Порядок E7, сбн(q) или E7, ad(q) (оба равны) можно получить, удалив коэффициент деления gcd (2, q−1) (последовательность A008869 в OEIS ). Множитель Шура для E7(q) является gcd (2, q−1), а его группа внешних автоморфизмов является произведением группы диагональных автоморфизмов Z/ gcd (2, q−1)Z (задается действием E7, ad(q)) и группу полевых автоморфизмов (т. е. циклических порядка ж если q = пж где п простое).
Важность в физике
N = 8 супергравитация в четырех измерениях, что является уменьшение размеров из 11-мерной супергравитации, допускаем E7 бозонная глобальная симметрия и SU (8) бозонный локальная симметрия. Фермионы находятся в представлениях SU (8), калибровочные поля - в представлении E7, а скаляры являются представлением обоих (гравитоны майки по отношению к обоим). Физические состояния в представлениях смежного класса E7 / SU (8).
В теория струн, E7 появляется как часть группа датчиков одного (нестабильного и нестабильногосуперсимметричный ) версии гетеротическая струна. Он также может появиться в непрерывной группе датчиков. E8 × E7 в шестимерных компактификациях гетеротической теории струн, например на четырехмерной поверхности K3.
Смотрите также
Заметки
- ^ Платонов, Владимир; Рапинчук, Андрей (1994) [1991], Алгебраические группы и теория чисел, Чистая и прикладная математика, 139, Бостон, Массачусетс: Академическая пресса, ISBN 978-0-12-558180-6, Г-Н 1278263 (оригинальная версия: Платонов, Владимир П .; Рапинчук, Андрей С. (1991). Алгебраические группы и теория чисел. Наука. ISBN 5-02-014191-7.), §2.2.4
- ^ Конвей, Джон Хортон; Кертис, Роберт Тернер; Нортон, Саймон Филлипс; Паркер, Ричард А; Уилсон, Роберт Арнотт (1985). Атлас конечных групп: Максимальные подгруппы и обыкновенные характеры для простых групп. Издательство Оксфордского университета. п. 46. ISBN 0-19-853199-0.
- ^ Картер, Роджер В. (1989). Простые группы лиева типа. Библиотека Wiley Classics. Джон Вили и сыновья. ISBN 0-471-50683-4.
- ^ Уилсон, Роберт А. (2009). Конечные простые группы. Тексты для выпускников по математике. 251. Springer-Verlag. ISBN 1-84800-987-9.
использованная литература
- Адамс, Дж. Франк (1996), Лекции об исключительных группах Ли, Чикагские лекции по математике, Издательство Чикагского университета, ISBN 978-0-226-00526-3, Г-Н 1428422
- Джон Баэз, Октонионы, Раздел 4.5: E7, Бык. Амер. Математика. Soc. 39 (2002), 145-205. Онлайн-версия HTML по адресу http://math.ucr.edu/home/baez/octonions/node18.html.
- Э. Креммер и Б. Джулия, В N = 8 Теория супергравитации. 1. Лагранжиан// Phys.Lett.B80: 48,1978. Отсканированная онлайн-версия по адресу http://ac.els-cdn.com/0370269378903039/1-s2.0-0370269378903039-main.pdf?_tid=79273f80-539d-11e4-a133-00000aab0f6c&acdnat=1413289833_5f3539a6365149b1092009ddcec.








![C_ {1} = pq-qp + Tr [PQ] -Tr [QP]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7710b7d259b59a9a6a8d8b18fcd632af7054eb6)
![C_ {2} = (pq + Tr [P circ Q]) ^ {2} + pTr [Q circ { tilde {Q}}] + qTr [P circ { tilde {P}}] + Tr [{ tilde {P}} circ { tilde {Q}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8e3fd1152c0065a4edbd173f1ddaf8b25964bd4)


![C_ {2} = Tr [(XY) ^ {2}] - { dfrac {1} {4}} Tr [XY] ^ {2} + { frac {1} {96}} epsilon _ {{ ijklmnop}} left (X ^ {{ij}} X ^ {{kl}} X ^ {{mn}} X ^ {{op}} + Y ^ {{ij}} Y ^ {{kl}} Y ^ {{mn}} Y ^ {{op}} right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/6282baf57eda5d68498c5eb85830709fa9484ee9)

