Строительство Wythoff - Wythoff construction

Витоффовские конструкции из 3-х зеркал, образующих прямоугольный треугольник.

В геометрия, а Строительство Wythoff, названный в честь математика Виллем Абрахам Витхофф, это метод построения равномерный многогранник или плоская черепица. Его часто называют калейдоскопический строительство.

Строительный процесс

Метод основан на идее черепица а сфера, с сферические треугольники - видеть Треугольники Шварца. В этой конструкции по сторонам треугольника расположены три зеркала, как в калейдоскоп. Однако, в отличие от калейдоскопа, зеркала не параллельны, а пересекаются в одной точке. Таким образом, они заключают сферический треугольник на поверхность любой сферы с центром в этой точке, и повторяющиеся отражения создают множество копий треугольника. Если углы сферического треугольника выбраны надлежащим образом, треугольники будут замощать сферу один или несколько раз.

Если поместить вершину в подходящую точку внутри сферического треугольника, окруженного зеркалами, можно гарантировать, что отражения этой точки образуют однородный многогранник. Для сферического треугольника ABC у нас есть четыре возможности, которые позволят создать однородный многогранник:

Вершина помещается в точку А. В результате получается многогранник с символом Wythoff. а|б c, куда а равно π, деленному на угол треугольника в А, и аналогично для б и c.
Вершина помещается в точку на линии AB так что это делит пополам угол при C. В результате получается многогранник с символом Wythoff. а б|c.
Вершина размещается так, чтобы она находилась на стимулятор из ABC. В результате получается многогранник с символом Wythoff. а б c|.
Вершина находится в такой точке, что при повороте вокруг любого из углов треугольника на удвоенный угол в этой точке она смещается на такое же расстояние для каждого угла. Используются только четные отражения исходной вершины. Многогранник имеет символ Витхоффа |а б c.

Этот процесс в целом также применим для многомерных правильные многогранники, в том числе 4-х мерный равномерные 4-многогранники.

Примеры
В шестиугольная призма состоит из семейств (6 2 2) и (3 2 2).	В усеченная квадратная мозаика строится по двум различным позициям симметрии в семействе (4 4 2).	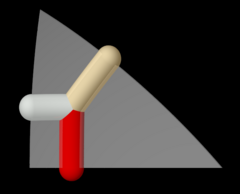Узор Wythoff pq2 \| = 432 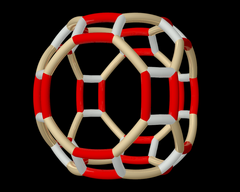\|. Орбита паттерна Wythoff выше под действием полного октаэдрическая группа .

Невитхоффовские конструкции

Равномерные многогранники которые не могут быть созданы с помощью конструкции зеркала Wythoff, называются non-Wythoffian. Обычно они могут быть получены из Wythoffian форм либо с помощью чередование (удаление чередующихся вершин) или вставкой чередующихся слоев частичных фигур. Оба этих типа фигур содержат вращательную симметрию. Иногда пренебрежительно формы считаются Wythoffian, хотя они могут быть построены только путем чередования полностью усеченных форм.

Примеры
В шестиугольная антипризма построен чередованием двенадцатигранная призма.	В удлиненно-треугольная черепица состоит из слоев квадратная черепица и треугольная черепица ряды.	В большой диромбикосододекаэдр является единственным однородным многогранником, отличным от Витофова.