Трапецоэдр - Trapezohedron
| Двойная униформа п-угольные трапецоэдры | |
|---|---|
 Пример двойного однородного десятиугольного трапеции | |
| Тип | двойной-униформа в смысле двойногополуправильный многогранник |
| Обозначение Конвея | dAп |
| Символ Шлефли | { } ⨁ {п}[1] |
| Диаграммы Кокстера | |
| Лица | 2п конгруэнтный воздушные змеи |
| Края | 4п |
| Вершины | 2п + 2 |
| Конфигурация лица | V3.3.3.п |
| Группа симметрии | Dпd, [2+,2п], (2*п), порядок 4п |
| Группа вращения | Dп, [2,п]+, (22п), порядок 2п |
| Двойной многогранник | (выпуклая) униформа п-гональный антипризма |
| Характеристики | выпуклый, лицо переходный, правильные вершины[2] |
В п-гональный трапецоэдр, антидипирамида, антибипирамида, или же дельтоэдр это двойственный многогранник из п-гональный антипризма. 2п лица п-трапецоэдры расположены симметрично в шахматном порядке. При более высокой симметрии его 2п лица конгруэнтный воздушные змеи (также называется дельтоидентификаторы).
В п-угольная часть имени здесь относится не к граням, а к двум расположениям вершин вокруг оси симметрии. Двойной п-гональная антипризма имеет два актуальных п-угольные грани.
An п-угольный трапецоэдр может быть рассеченный на два равных п-угольные пирамиды и п-гональный антипризма.
Имя
Эти цифры, иногда называемые дельтоHedra, не следует путать с дельтааHedra, грани которого представляют собой равносторонние треугольники.
В кристаллография, описывая кристальные привычки из минералы, слово трапецоэдр часто используется для обозначения многогранника, известного как дельтовидный икоситетраэдр; другой многогранник известен как дельтовидный додекаэдр.[3]
Симметрия
В группа симметрии из п-угольный трапецииэдр - Dпd порядка 4п, за исключением куба, который имеет большую группу симметрии Od порядка 48, который имеет четыре версии D3D как подгруппы.
В группа ротации это Dп порядка 2п, за исключением случая куба, который имеет большую группу вращения O порядка 24, который имеет четыре версии D3 как подгруппы.
Одна степень свободы в пределах симметрии от Dпd (заказ 4п) в Dп (заказ 2п) превращает конгруэнтные воздушные змеи в конгруэнтные четырехугольники с тремя длинами ребер, называемые витые змеи, а трапецоэдр называется витой трапецииэдр. (В пределе одно ребро каждого четырехугольника переходит в нулевую длину, а трапецоэдр становится бипирамида.)
Если воздушные змеи, окружающие две вершины, не скручены, а имеют две разные формы, трапецоэдр может иметь только Cпv (циклическая) симметрия, порядок 2п, и называется неравный или же асимметричный трапецоэдр. Его дуал - это неравный антипризма, с верхним и нижним многоугольниками разного радиуса.
Если воздушные змеи скручены и имеют две разные формы, трапецоэдр может иметь только Cп (циклическая) симметрия, порядок п, и называется неравномерно закрученный трапецоэдр.
| Тип | Скрученный трапецоэдр | Неравный трапецоэдр | Неравномерно закрученный трапецоэдр | |
|---|---|---|---|---|
| Симметрия | Dп, (nn2), [п,2]+ | Cпv, (*nn), [п] | Cп, (nn), [п]+ | |
| Изображение (п=6) | 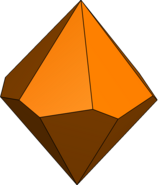 |  |  |  |
| Сеть |  | 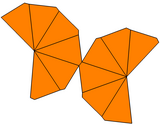 | 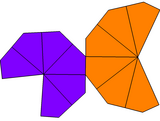 |  |
Формы
А п-трапецоэдр имеет 2п четырехугольные грани, с 2п+2 вершины. Две вершины находятся на полярной оси, а остальные - в двух правильных п-гональные кольца вершин.
| Семья п-гональный трапецоэдры | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника |  |  |  |  |  |  |  |  | ... | Апейрогональный трапецоэдр | |
| Сферическое мозаичное изображение |  |  |  |  |  |  |  |  | Плоское мозаичное изображение | ||
| Конфигурация лица Vп.3.3.3 | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
Особые случаи:
- п= 2: Вырожденная форма трапецоэдра: геометрическая тетраэдр с 6 вершинами, 8 ребрами и 4 вырожденными летающий змей лица, которые вырожденыd в треугольники. Его двойник является вырожденной формой антипризма: также тетраэдр.
- п= 3: в случае двойственного треугольная антипризма, воздушные змеи ромбовидные (или квадратные); следовательно, эти трапецоэдры тоже зоноэдры. Они называются ромбоэдры. Они есть кубики масштабируется в направлении диагонали тела. Также они параллелепипеды с конгруэнтными ромбическими гранями.
 Ромбоэдр 60 °, рассеченный в центральный правильный октаэдр и два правильных тетраэдра
Ромбоэдр 60 °, рассеченный в центральный правильный октаэдр и два правильных тетраэдра- Особым случаем ромбоэдра является тот, в котором ромбы, образующие грани, имеют углы 60 ° и 120 °. Его можно разложить на два равных правильных тетраэдра и правильный октаэдр. Поскольку параллелепипеды могут заполнить пространство, так может сочетание правильных тетраэдров и правильных октаэдров.
Примеры
- Хрустальные композиции атомов могут повторяться в пространстве с тригональными и гексагональными трапециевидными ячейками.[4]
- В пятиугольный трапецииэдр единственный многогранник кроме Платоновы тела обычно используется как умереть в ролевые игры Такие как Подземелья и Драконы. Имея 10 сторон, его можно повторять для создания любых десятичных чисел. равномерная вероятность желанный. Два кубика разных цветов обычно используются для двух цифры для представления чисел от 00 до 99.
Звездные трапецоэдры
Самопересекающиеся трапецоэдры существуют с звездный многоугольник центральная фигура, определяемая летающий змей грани, соединяющие каждое ребро многоугольника с этими двумя точками. А п/q-трапецоэдр имеет Диаграмма Кокстера-Дынкина ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 5/2 | 5/3 | 7/2 | 7/3 | 7/4 | 8/3 | 8/5 | 9/2 | 9/4 | 9/5 |
|---|---|---|---|---|---|---|---|---|---|
| 10/3 | 11/2 | 11/3 | 11/4 | 11/5 | 11/6 | 11/7 | 12/5 | 12/7 | |
Смотрите также
- Уменьшенный трапецоэдр
- Ромбический додекаэдр
- Ромбический триаконтаэдр
- Бипирамида
- Усеченный трапецоэдр
- Обозначения многогранника Конвея
- Призрак тьмы, рассказ H.P. Лавкрафт в котором вымышленный древний артефакт, известный как Сияющий Трапецоэдр, играет решающую роль.
Рекомендации
- ^ N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3c
- ^ "двойственность". maths.ac-noumea.nc. Получено 2020-10-19.
- ^ "Британская энциклопедия 1911 г. / Кристаллография - Wikisource, бесплатная онлайн-библиотека". en.m.wikisource.org. Получено 2020-11-16.
- ^ Тригонально-трапецоэдрический класс, 3 2 и гексагонально-трапецоэдрический класс, 6 2 2
- Энтони Пью (1976). Многогранники: визуальный подход. Калифорния: Калифорнийский университет Press в Беркли. ISBN 0-520-03056-7. Глава 4: Двойники архимедовых многогранников, призмы и антипризмы
внешняя ссылка
- Вайсштейн, Эрик В. «Трапецоэдр». MathWorld.
- Вайсштейн, Эрик В. "Изогедр". MathWorld.
- Многогранники виртуальной реальности Энциклопедия многогранников
- VRML модели (Джордж Харт) <3> <4> <5> <6> <7> <8> [постоянная мертвая ссылка ] <9> <10>
- Обозначение Конвея для многогранников Попробуйте: "dAп", куда п= 3,4,5 ... пример "dA5" - пятиугольный трапецииэдр.
- Бумажная модель тетрагональный (квадратный) трапецоэдр

