Список апериодических наборов плиток - List of aperiodic sets of tiles

В геометрия, а черепица представляет собой разбиение плоскости (или любого другого геометрического объекта) на замкнутые множества (называемые плитка), без пропусков и нахлёстков (кроме границ плитки).[1] Тайлинг считается периодическим, если существуют сдвиги в двух независимых направлениях, которые отображают тайлинг на себя. Такая плитка состоит из одного основная единица или же примитивная клетка который повторяется бесконечно и регулярно в двух независимых направлениях.[2] Пример такой мозаики показан на диаграмме рядом (дополнительную информацию см. В описании изображения). Мозаика, которую невозможно построить из одной примитивной ячейки, называется непериодической. Если данный набор плиток допускает только непериодические мозаики, то этот набор плиток называется апериодический.[3] Замощения, полученные из апериодического набора плиток, часто называют апериодические мозаики, хотя, строго говоря, апериодическими являются сами плитки. (Сама мозаика называется «непериодической».)
В первой таблице поясняются сокращения, используемые во второй таблице. Вторая таблица содержит все известные апериодические наборы плиток и дает некоторую дополнительную базовую информацию о каждом наборе. Этот список плиток еще неполный.
Пояснения
| Сокращение | Смысл | Объяснение |
|---|---|---|
| E2 | Евклидова плоскость | нормальная плоская плоскость |
| ЧАС2 | гиперболическая плоскость | самолет, где параллельный постулат не держит |
| E3 | Евклидово пространство 3 | пространство, определяемое тремя перпендикулярными осями координат |
| MLD | Взаимно локально выводимые | две мозаики называются взаимно локально производными друг от друга, если одна мозаика может быть получена из другой с помощью простого локального правила (например, удаления или вставки ребра) |
Список
| Изображение | Имя | Количество плиток | Космос | Дата публикации | Ссылка | Комментарии |
|---|---|---|---|---|---|---|
 | Трилобиты и крестовые плитки | 2 | E2 | 1999 | [4] | Плитки МЛД от стула |
 | Плитка Penrose P1 | 6 | E2 | 1974[5] | [6] | Плитки MLD из мозаик P2 и P3, треугольников Робинсона и "Морская звезда, лист плюща, шестигранник" |
 | Плитка Penrose P2 | 2 | E2 | 1977[7] | [8] | Тайлинги MLD из мозаик P1 и P3, треугольников Робинсона и "Морская звезда, лист плюща, шестигранник" |
 | Плитка Penrose P3 | 2 | E2 | 1978[9] | [10] | Плитки MLD из мозаик P1 и P2, треугольников Робинсона и "Морская звезда, лист плюща, шестигранник" |
 | Бинарные плитки | 2 | E2 | 1988 | [11][12] | Хотя мозаики похожи по форме на плитки P3, они не отличаются друг от друга MLD. Разработан в попытке смоделировать расположение атомов в бинарных сплавах. |
 | Плитки Робинзона | 6 | E2 | 1971[13] | [14] | Плитки усиливают апериодичность, образуя бесконечную иерархию квадратных решеток. |
| Нет изображения | Плитка Ammann A1 | 6 | E2 | 1977[15] | [16] | Плитки усиливают апериодичность, формируя бесконечное иерархическое двоичное дерево. |
 | Плитка Ammann A2 | 2 | E2 | 1986[17] | [18] | |
 | Плитка Ammann A3 | 3 | E2 | 1986[17] | [18] | |
 | Плитка Ammann A4 | 2 | E2 | 1986[17] | [18][19] | Плитки MLD с Ammann A5. |
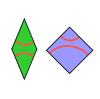 | Плитка Ammann A5 | 2 | E2 | 1982[20] | [21][22] | Плитки MLD с Ammann A4. |
| Нет изображения | Шестиугольник-треугольник Пенроуза | 2 | E2 | 1997[23] | [23][24] | |
 | Золотой треугольник плитка | 10 | E2 | 2001[25] | [26] | дата предназначена для обнаружения правил соответствия. Двойной к Ammann A2 |
 | Социальные плитки | 3 | E2 | 1989[27] | [28][29] | Плитки МЛД из плиток Щит |
 | Щитовые плитки | 4 | E2 | 1988[30] | [31][32] | Тайлинги MLD из мозаик соколарными плитками |
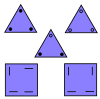 | Квадратные треугольные плитки | 5 | E2 | 1986[33] | [34] | |
 | Морская звезда, лист плюща и шестигранные плитки | 3 | E2 | [35][36][37] | Мозаика - это MLD в треугольники Пенроуза P1, P2, P3 и Робинсона. | |
 | Треугольник Робинсона | 4 | E2 | [17] | Мозаика - это MLD для P1, P2, P3 Пенроуза и «Морская звезда, лист плюща, шестигранник». | |
 | Данцеровские треугольники | 6 | E2 | 1996[38] | [39] | |
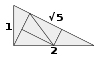 | Вертушка плитки | E2 | 1994[40][41] | [42][43] | Дата публикации правил соответствия. | |
 | Плитка Socolar – Taylor | 1 | E2 | 2010 | [44][45] | Не подключенный набор. Апериодическая иерархическая мозаика. |
| Нет изображения | Ванская плитка | 20426 | E2 | 1966 | [46] | |
| Нет изображения | Ванская плитка | 104 | E2 | 2008 | [47] | |
| Нет изображения | Ванская плитка | 52 | E2 | 1971[13] | [48] | Плитки усиливают апериодичность, образуя бесконечную иерархию квадратных решеток. |
 | Ванская плитка | 32 | E2 | 1986 | [49] | Производится локально из плиток Пенроуза. |
| Нет изображения | Ванская плитка | 24 | E2 | 1986 | [49] | Локально выводится из тайлинга A2 |
 | Ванская плитка | 16 | E2 | 1986 | [17][50] | Получено из тайлинга A2 и его стержней Аммана |
 | Ванская плитка | 14 | E2 | 1996 | [51][52] | |
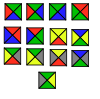 | Ванская плитка | 13 | E2 | 1996 | [53][54] | |
 | Ванская плитка | 11 | E2 | 2015 | [55] | |
| Нет изображения | Десятиугольная плитка из губки | 1 | E2 | 2002 | [56][57] | Пористая плитка, состоящая из неперекрывающихся наборов точек |
| Нет изображения | Сильно апериодические плитки Гудмана-Штрауса | 85 | ЧАС2 | 2005 | [58] | |
| Нет изображения | Сильно апериодические плитки Гудмана-Штрауса | 26 | ЧАС2 | 2005 | [59] | |
 | Гиперболическая черепица Бёрёчки | 1 | ЧАСп | 1974[60][61] | [59][62] | Только слабо апериодический |
| Нет изображения | Плитка Шмитта | 1 | E3 | 1988 | [63] | Винтовой периодический |
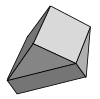 | Плитка Шмитта – Конвея – Данцера | 1 | E3 | [63] | Винтовой периодический и выпуклый | |
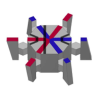 | Плитка Socolar – Taylor | 1 | E3 | 2010 | [44][45] | Периодический в третьем измерении |
| Нет изображения | Ромбоэдры Пенроуза | 2 | E3 | 1981[64] | [65][66][67][68][69][70][71] | |
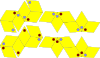 | Ромбоэдры Маккая – Аммана | 4 | E3 | 1981 | [35] | Икосаэдрическая симметрия. Это декорированные ромбоэдры Пенроуза с правилом согласования, обеспечивающим апериодичность. |
| Нет изображения | Кубики Ванга | 21 | E3 | 1996 | [72] | |
| Нет изображения | Кубики Ванга | 18 | E3 | 1999 | [73] | |
| Нет изображения | Данцеровские тетраэдры | 4 | E3 | 1989[74] | [75] | |
 | I и L плитки | 2 | Eп для всех n ≥ 3 | 1999 | [76] |
Рекомендации
- ^ Грюнбаум, Бранко; Шепард, Джеффри К. (1977), "Замощения правильными многоугольниками", Математика. Mag., 50 (5): 227–247, Дои:10.2307/2689529, JSTOR 2689529
- ^ Эдвардс, Стив, «Фундаментальные области и примитивные клетки», Самолет плитки и фантазии, Государственный университет Кеннесо, в архиве из оригинала от 16.09.2010, получено 2017-01-11
- ^ Вагон, Стив (2010), Mathematica в действии (3-е изд.), Springer Science & Business Media, стр. 268, ISBN 9780387754772
- ^ Гудман-Штраус, Хаим (1999), "Небольшой апериодический набор плоских плиток", Европейский J. Combin., 20 (5): 375–384, Дои:10.1006 / eujc.1998.0281 (препринт доступен )
- ^ Пенроуз, Роджер (1974), «Роль эстетики в чисто и прикладных математических исследованиях», Бык. Inst. Математика. И его приложение., 10 (2): 266–271
- ^ Михаэль, Жюль (2010), Коллоидные монослои на квазипериодических лазерных полях. (PDF) (Докторская диссертация), стр. 23, Дои:10.18419 / opus-4924, в архиве (PDF) из оригинала 28.09.2010
- ^ Гарднер, Мартин (Январь 1977 г.), «Математические игры: необычные непериодические мозаики, обогащающие теорию плиток», Scientific American, 236 (1): 110–121, Bibcode:1977SciAm.236a.110G, Дои:10.1038 / scientificamerican0177-110
- ^ Гарднер, Мартин (1997), Плитки Пенроуза для тайных шифров (Пересмотренное издание), The Mathematical Association of America, p. 86, ISBN 9780883855218
- ^ Пенроуз, Роджер (1978), «Пентаплексичность», Эврика, 39: 16–22
- ^ Пенроуз, Роджер (1979), «Пентаплексити», Математика. Intell., 2 (1): 32–37, Дои:10.1007 / bf03024384, S2CID 120305260, в архиве из оригинала от 23.09.2010, получено 2010-07-26
- ^ Lançon, F .; Биллард, Л. (1988), «Двумерная система с квазикристаллическим основным состоянием» (PDF), Journal de Physique, 49 (2): 249–256, CiteSeerX 10.1.1.700.3611, Дои:10.1051 / jphys: 01988004902024900, в архиве (PDF) из оригинала от 29.09.2010
- ^ Годреш, С .; Лансон, Ф. (1992), «Простой пример мозаики Пизо с пятикратной симметрией» (PDF), Journal de Physique I, 2 (2): 207–220, Bibcode:1992JPhy1 ... 2..207G, Дои:10.1051 / jp1: 1992134, в архиве (PDF) из оригинала от 29.09.2010
- ^ а б Робинсон, Рафаэль М. (1971), "Неразрешимость и непериодичность мозаик на плоскости", Inventiones Mathematicae, 12 (3): 177–209, Bibcode:1971InMat..12..177R, Дои:10.1007 / BF01418780, S2CID 14259496
- ^ Goodman-Strauss, Chaim (1999), Sadoc, J. F .; Ривье, Н. (ред.), "Апериодические иерархические мозаики", Серия НАТО ASI, Серия E: Прикладные науки, 354 (Пены и эмульсии): 481–496, Дои:10.1007/978-94-015-9157-7_28, ISBN 978-90-481-5180-6
- ^ Гарднер, Мартин (2001), Колоссальная книга математики, W. W. Norton & Company, стр. 76, ISBN 978-0393020236
- ^ Грюнбаум, Бранко И Шепард, Джеффри К. (1986), Плитки и узоры, Нью-Йорк: В. Х. Фриман, ISBN 978-0-7167-1194-0, в соответствии с Датч, Стивен (2003), Апериодические мозаики, Университет Висконсина - Грин Бэй, архивировано из оригинал на 2006-08-30, получено 2011-04-02; ср. Савард, Джон Дж. Г., Апериодические мозаики внутри обычных решеток
- ^ а б c d е Грюнбаум, Бранко И Шепард, Джеффри К. (1986), Плитки и узоры, Нью-Йорк: В. Х. Фриман, ISBN 978-0-7167-1194-0
- ^ а б c Амманн, Роберт; Грюнбаум, Бранко; Шепард, Джеффри К. (июль 1992 г.), «Апериодические плитки», Дискретная и вычислительная геометрия, 8 (1): 1–25, Дои:10.1007 / BF02293033, S2CID 39158680
- ^ Харрис, Эдмунд; Фреттлё, Дирк, «Амманн А4», Энциклопедия Тилингса, Билефельдский университет
- ^ Бинкер, Ф. П. М. (1982), Алгебраическая теория непериодических мозаик плоскости двумя простыми кирпичиками: квадратом и ромбом, Отчет TH, 82-WSK04, Технологический университет Эйндховена
- ^ Комацу, Казуши; Номакучи, Кентаро; Сакамото, Кунико; Токито, Такаши (2004), "Представление мозаик Амманна-Бенкера автоматом", Nihonkai Math. Дж., 15 (2): 109–118, в архиве из оригинала от 29.09.2010, получено 2017-01-12
- ^ Харрис, Эдмунд; Фреттлё, Дирк, «Амманн-Бенкер», Энциклопедия Тилингса, Билефельдский университет
- ^ а б Пенроуз, Р. (1997), "Замечания о мозаике: детали (1 + ε + ε2) апериодический набор. ", Серия НАТО ASI, Серия C: Математические и физические науки, 489 (Математика дальнего апериодического порядка): 467–497, Дои:10.1007/978-94-015-8784-6_18, ISBN 978-0-7923-4506-0
- ^ Гудман-Штраус, Хаим (2003), Апериодическая пара плиток (PDF), Университет Арканзаса
- ^ Данцер, Людвиг; van Ophuysen, Gerrit (2001), "Вид плоских треугольных плиток с коэффициентом инфляции ", Res. Бык. Panjab Univ. Sci., 50 (1–4): 137–175, МИСТЕР 1914493
- ^ Гелбрих, G (1997), "Фрактальные плитки Пенроуза II. Плитки с фрактальной границей как двойники треугольников Пенроуза", Aequationes Mathematicae, 54 (1–2): 108–116, Дои:10.1007 / bf02755450, МИСТЕР 1466298, S2CID 120531480
- ^ Соколар, Джошуа Э. С. (1989), "Простые восьмиугольные и додекагональные квазикристаллы", Физический обзор B, 39 (15): 10519–51, Bibcode:1989PhRvB..3910519S, Дои:10.1103 / PhysRevB.39.10519, PMID 9947860
- ^ Гелер, Франц; Люк, Рейнхард; Бен-Авраам, Шеломо I .; Гуммельт, Петра (2001), "Додекагональные мозаики как максимальные кластерные покрытия", Сегнетоэлектрики, 250 (1): 335–338, Дои:10.1080/00150190108225095, S2CID 123171399
- ^ Савард, Джон Дж. Г., Социальная мозаика
- ^ Гелер, Франц (1988), «Кристаллография додекагональных квазикристаллов."" (PDF), в Janot, Christian (ed.), Квазикристаллические материалы: Труды I.L.L. / Codest Workshop, Гренобль, 21–25 марта 1988 г., Сингапур: World Scientific, стр. 272–284.
- ^ Гелер, Франц; Фреттлё, Дирк, "Щит", Энциклопедия Тилингса, Билефельдский университет
- ^ Гелер, Франц (1993), «Правила согласования для квазикристаллов: метод разложения по составу». (PDF), Журнал некристаллических твердых тел, 153–154 (Протоколы Четвертой Международной конференции по квазикристаллам): 160–164, Bibcode:1993JNCS..153..160G, CiteSeerX 10.1.1.69.2823, Дои:10.1016 / 0022-3093 (93) 90335-у, в архиве (PDF) с оригинала от 01.10.2010
- ^ Stampfli, P. (1986), "Додекагональная квазипериодическая решетка в двух измерениях", Helv. Phys. Acta, 59: 1260–1263
- ^ Гермиссон, Иоахим; Ричард, Кристоф; Бааке, Майкл (1997), "Руководство по структуре симметрии квазипериодических классов тайлинга", Journal de Physique I, 7 (8): 1003–1018, Bibcode:1997JPhy1 ... 7.1003H, CiteSeerX 10.1.1.46.5796, Дои:10.1051 / jp1: 1997200
- ^ а б Господи, Эрик. А. (1991), «Квазикристаллы и узоры Пенроуза» (PDF), Текущая наука, 61 (5): 313–319, в архиве (PDF) из оригинала 27 сентября 2010 г.
- ^ Олами, З .; Клеман, М. (1989), «Двумерный апериодический плотный тайлинг» (PDF), Journal de Physique, 50 (1): 19–33, Дои:10.1051 / jphys: 0198900500101900, в архиве (PDF) из оригинала 01.11.2010
- ^ Михалкович, М .; Henley, C.L .; Видом, М. (2004), "Комбинированное уточнение данных дифракции энергии декагонального AlNiCo", Журнал некристаллических твердых телС. 334–335 (8-я Международная конференция по квазикристаллам): 177–183, arXiv:cond-mat / 0311613, Bibcode:2004JNCS..334..177M, Дои:10.1016 / j.jnoncrysol.2003.11.034, S2CID 18958430
- ^ Nischke, K.-P .; Данзер, Л. (1996), "Построение правил инфляции на основе п-кратная симметрия », Дискретная и вычислительная геометрия, 15 (2): 221–236, Дои:10.1007 / bf02717732, S2CID 22538367
- ^ Хаяси, Хироко; Кавачи, Юу; Комацу, Казуши; Конда, Ая; Курозоэ, Михо; Накано, Фумихико; Одавара, Наоми; Онда, Рика; Сугио, Акинобу; Ямаути, Масатэцу (2009), "Аннотация: Примечания к атласу вершин плоской мозаики Данцера" (PDF), Японская конференция по вычислительной геометрии и графам, Канадзава, 11–13 ноября 2009 г.
- ^ Радин, Чарльз (1994), "Вертушки на плоскости", Анналы математики, Вторая серия, 139 (3): 661–702, CiteSeerX 10.1.1.44.9723, Дои:10.2307/2118575, JSTOR 2118575, МИСТЕР 1283873
- ^ Радин, Чарльз (1993), "Симметрия мозаик на плоскости", Бык. Амер. Математика. Soc., 29 (2): 213–217, arXiv:математика / 9310234, Bibcode:1993математика ..... 10234R, CiteSeerX 10.1.1.45.5319, Дои:10.1090 / s0273-0979-1993-00425-7, S2CID 14935227
- ^ Радин, Чарльз; Вольф, Мэйхью (1992), "Пространственные мозаики и локальный изоморфизм", Геом. Dedicata, 42 (3): 355–360, Дои:10.1007 / bf02414073, МИСТЕР 1164542, S2CID 16334831
- ^ Радин, C (1997), "Апериодические мозаики, эргодическая теория и вращения", Серия НАТО ASI, Серия C: Математические и физические науки, Kluwer Acad. Publ., Dordrecht, 489 (Математика дальнего апериодического порядка), МИСТЕР 1460035
- ^ а б Socolar, Джошуа Э. С .; Тейлор, Джоан М. (2011), «Апериодическая шестиугольная плитка», Журнал комбинаторной теории, серия А, 118 (8): 2207–2231, arXiv:1003.4279v1, Дои:10.1016 / j.jcta.2011.05.001, S2CID 27912253
- ^ а б Socolar, Джошуа Э. С .; Тейлор, Джоан М. (2011), «Принудительная непериодичность с помощью одной плитки», Математический интеллект, 34 (1): 18–28, arXiv:1009.1419v1, Дои:10.1007 / s00283-011-9255-у, S2CID 10747746
- ^ Бургер, Роберт (1966), "Неразрешимость проблемы домино", Мемуары Американского математического общества, 66 (66), Дои:10.1090 / memo / 0066, ISBN 978-0-8218-1266-2
- ^ Оллингер, Николас (2008), «Системы подстановки два на два и неразрешимость проблемы домино» (PDF), Логика и теория алгоритмов, Конспект лекций по информатике, 5028, Springer, стр. 476–485, CiteSeerX 10.1.1.371.9357, Дои:10.1007/978-3-540-69407-6_51, ISBN 978-3-540-69405-2
- ^ Кари, Дж.; Папасоглу П. (1999), "Детерминированные апериодические мозаичные наборы", Геометрический и функциональный анализ, 9 (2): 353–369, Дои:10.1007 / с000390050090, S2CID 8775966
- ^ а б Лагаэ, Арес; Кари, Яркко; Дютре, Филипп (2006), Апериодические наборы квадратных плиток с цветными углами, Отчет CW, 460, KU Leuven, п. 15, CiteSeerX 10.1.1.89.1294
- ^ Карбоне, Алессандра; Громов, Михаил; Прусинкевич, Пшемыслав (2000), Формирование паттернов в биологии, зрении и динамике, Сингапур: World Scientific, ISBN 978-981-02-3792-9
- ^ Кари, Яркко (1996), "Небольшой апериодический набор плиток Ванга", Дискретная математика, 160 (1–3): 259–264, Дои:10.1016 / 0012-365X (95) 00120-L
- ^ Лагаэ, Арес (2007), Тайловые методы в компьютерной графике (PDF) (Кандидатская диссертация), KU Leuven, п. 149, ISBN 978-90-5682-789-2, заархивировано из оригинал (PDF) на 2010-10-06
- ^ Кулик, Карел; Кари, Яркко (1997), "Об апериодических наборах плиток Ванга", Основы информатики, Конспект лекций по информатике, 1337, стр. 153–162, Дои:10.1007 / BFb0052084, ISBN 978-3-540-63746-2
- ^ Кулик, Карел (1996), "Апериодический набор из 13 плиток Ванга", Дискретная математика, 160 (1–3): 245–251, CiteSeerX 10.1.1.53.5421, Дои:10.1016 / S0012-365X (96) 00118-5
- ^ Джендель, Эммануэль; Рао, Майкл (2015), «Апериодический набор из 11 плиток Ванга», CoRR, arXiv:1506.06492, Bibcode:2015arXiv150606492J
- ^ Чжу, Фэн (2002), В поисках универсальной плитки (PDF) (Дипломная работа), Колледж Уильямса
- ^ Bailey, Duane A .; Чжу, Фэн (2001), Губчатая (почти) универсальная плитка (PDF), CiteSeerX 10.1.1.103.3739
- ^ Гудман-Штраус, Хаим (2010), «Иерархический сильно апериодический набор плиток в гиперболической плоскости» (PDF), Теоретическая информатика, 411 (7–9): 1085–1093, Дои:10.1016 / j.tcs.2009.11.018
- ^ а б Гудман-Штраус, Хаим (2005), "Сильно апериодический набор плиток в гиперболической плоскости", Изобретать. Математика., 159 (1): 130–132, Bibcode:2004InMat.159..119G, CiteSeerX 10.1.1.477.1974, Дои:10.1007 / s00222-004-0384-1, S2CID 5348203
- ^ Бёрёчки К. (1974), "Gömbkitöltések állandó görbületü terekben I", Математикай Лапок, 25: 265–306
- ^ Бёрёчки К. (1974), "Gömbkitöltések állandó görbületü terekben II", Математикай Лапок, 26: 67–90
- ^ Долбилин, Никколай; Фреттлё, Дирк (2010), «Свойства мозаик Бёрёчки в гиперболических пространствах большой размерности» (PDF), Европейский J. Combin., 31 (4): 1181–1195, arXiv:0705.0291, CiteSeerX 10.1.1.246.9821, Дои:10.1016 / j.ejc.2009.11.016, S2CID 13607905
- ^ а б Радин, Чарльз (1995), «Апериодические мозаики в высших измерениях» (PDF), Труды Американского математического общества, Американское математическое общество, 123 (11): 3543–3548, Дои:10.2307/2161105, JSTOR 2161105, получено 2013-09-25
- ^ Маккей, Алан Л. (1981), "De Nive Quinquangula: На пятиугольной снежинке" (PDF), Сов. Phys. Кристаллогр., 26 (5): 517–522, в архиве (PDF) с оригинала от 06.10.2010
- ^ Мейстерернст, Гётц, Experimente zur Wachstumskinetik Dekagonaler Quasikristalle (PDF) (Диссертация), Мюнхенский университет Людвига-Максимилиана, стр. 18–19, в архиве (PDF) из оригинала от 08.10.2010
- ^ Джиронг, Сан (1993), "Структурный переход трехмерной мозаики Пенроуза в фазовом поле деформации", Китайская физ. Lett., 10 (8): 449–452, Bibcode:1993ЧФЛ..10..449С, Дои:10.1088 / 0256-307x / 10/8/001
- ^ Инчбальд, Гай (2002), Трехмерная квазикристаллическая структура
- ^ Лорд, Э. А .; Ranganathan, S .; Кулькарни, У. Д. (2001), «Квазикристаллы: мозаика против кластеризации» (PDF), Философский журнал А, 81 (11): 2645–2651, Bibcode:2001ПМагА..81.2645Л, CiteSeerX 10.1.1.487.2640, Дои:10.1080/01418610108216660, S2CID 138403519, в архиве (PDF) с оригинала от 06.10.2010
- ^ Рудхарт, Кристоф Пол (июнь 1999 г.), Zur numerischen Simulation des Bruchs von Quasikristallen (Тезис), Штутгартский университет, п. 11, Дои:10.18419 / opus-4639
- ^ Лорд, Э. А .; Ranganathan, S .; Кулькарни, У. Д. (2000), «Тайлинги, покрытия, кластеры и квазикристаллы» (PDF), Текущая наука, 78 (1): 64–72, в архиве (PDF) из оригинала 01.11.2010
- ^ Кац, А. (1988), "Теория соответствия правил для трехмерных мозаик Пенроуза", Коммуникации по математической физике, 118 (2): 263–288, Bibcode:1988CMaPh.118..263K, Дои:10.1007 / BF01218580, S2CID 121086829
- ^ Кулик, Карел; Кари, Яркко (1995), «Апериодический набор кубиков Ванга», Журнал универсальных компьютерных наук, 1 (10), CiteSeerX 10.1.1.54.5897, Дои:10.3217 / jucs-001-10-0675
- ^ Вальтер. Герд; Селтер, Кристоф, ред. (1999), Математика и наука о дизайне: Festschrift für Erich Christian Wittmann, Лейпциг: Ernst Klett Grundschulverlag, ISBN 978-3-12-200060-8
- ^ Данзер, Л. (1989), "Трехмерные аналоги плоских мозаик Пенроуза и квазикристаллов", Дискретная математика, 76 (1): 1–7, Дои:10.1016 / 0012-365X (89) 90282-3
- ^ Церхузен, Аарон (1997), Трехмерная плитка Данцера, Университет Кентукки
- ^ Гудман-Штраус, Хаим (1999), "Апериодическая пара плиток в Eп для всех n ≥ 3 ", Европейский J. Combin., 20 (5): 385–395, Дои:10.1006 / eujc.1998.0282 (препринт доступен )
внешняя ссылка
- Стивенс П. В., Гольдман А. И. Структура квазикристаллов.
- Левин Д., Стейнхардт П. Дж. Квазикристаллы I Определение и структура.
- Энциклопедия Тилингса



