Тессеракт - Tesseract
| Тессеракт 8-элементный 4-куб | |
|---|---|
 | |
| Тип | Выпуклый правильный 4-многогранник |
| Символ Шлефли | {4,3,3} т0,3{4,3,2} или {4,3} × {} т0,2{4,2,4} или {4} × {4} т0,2,3{4,2,2} или {4} × {} × {} т0,1,2,3{2,2,2} или {} × {} × {} × {} |
| Диаграмма Кокстера | |
| Клетки | 8 {4,3} |
| Лица | 24 {4} |
| Края | 32 |
| Вершины | 16 |
| Фигура вершины |  Тетраэдр |
| Многоугольник Петри | восьмиугольник |
| Группа Коксетера | B4, [3,3,4] |
| Двойной | 16 ячеек |
| Характеристики | выпуклый, изогональный, изотоксальный, равногранный |
| Единый индекс | 10 |

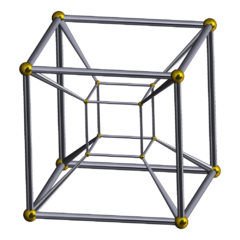
В геометрия, то тессеракт это четырехмерный аналог куб; тессеракт для куба, как куб для квадрат.[1] Так же, как поверхность куба состоит из шести квадратных лица, то гиперповерхность тессеракта состоит из восьми кубических клетки. Тессеракт - один из шести выпуклые правильные 4-многогранники.
Тессеракт также называют восьмикамерный, C8, (обычный) октахорон, октаэдроид,[2] кубическая призма, и тетракуб.[3] Это четырехмерный гиперкуб, или же 4-куб как часть размерного семейства гиперкубы или же измерять многогранники.[4] Коксетер называет это многогранник.[5] Термин «гиперкуб» без ссылки на размер часто рассматривается как синоним этой конкретной формы.
Согласно Оксфордский словарь английского языка, слово тессеракт был придуман и впервые использован в 1888 г. Чарльз Ховард Хинтон в его книге Новая эра мысли, от Греческий τέσσερεις ἀκτίνες (téssereis aktínes, «четыре луча»), относящиеся к четырем линиям от каждой вершины к другим вершинам.[6] В этой публикации, а также в некоторых более поздних работах Хинтона слово иногда пишется как «тессаракт».
Геометрия
Тессеракт можно построить разными способами. Как правильный многогранник с тремя кубики сложенный по каждому краю, он имеет Символ Шлефли {4,3,3} с гипероктаэдрическая симметрия порядка 384. Построен как 4D гиперпризма состоящий из двух параллельных кубов, его можно назвать составным Символ Шлефли {4,3} × {}, с порядком симметрии 96. Как 4-4 дуопризма, а Декартово произведение из двух квадраты, его можно назвать составным символом Шлефли {4} × {4} с порядком симметрии 64. Как ортотоп он может быть представлен составным символом Шлефли {} × {} × {} × {} или {}4, с порядком симметрии 16.
Поскольку каждая вершина тессеракта смежна с четырьмя ребрами, вершина фигуры тессеракта - обычный тетраэдр. В двойственный многогранник тессеракта называется регулярным гексадекахорон, или 16-элементный, с символом Шлефли {3,3,4}, с которым его можно комбинировать, чтобы сформировать соединение тессеракта и 16 ячеек.
Стандартный тессеракт в Евклидово 4-мерное пространство дается как выпуклый корпус точек (± 1, ± 1, ± 1, ± 1). То есть состоит из точек:
Тессеракт ограничен восемью гиперплоскости (Икся = ± 1). Каждая пара непараллельных гиперплоскостей пересекается, образуя 24 квадратных грани в тессеракте. По каждому краю пересекаются по три кубика и три квадрата. Четыре куба, шесть квадратов и четыре ребра пересекаются в каждой вершине. Всего он состоит из 8 кубиков, 24 квадратов, 32 ребер и 16 вершин.
Проекции в двух измерениях

Построение гиперкубы можно представить следующим образом:
- 1-мерный: Две точки A и B можно соединить в линию, образуя новый отрезок AB.
- 2-х мерный: Два параллельных отрезка AB и CD могут быть соединены в квадрат с углами, отмеченными как ABCD.
- 3-х мерный: Два параллельных квадрата ABCD и EFGH можно соединить в куб с углами, обозначенными как ABCDEFGH.
- 4-х мерный: Два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены в тессеракт с углами, отмеченными как ABCDEFGHIJKLMNOP.
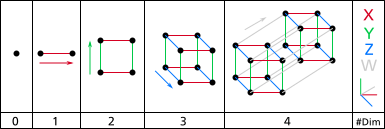

Можно проецировать тессеракты в трехмерные и двумерные пространства, аналогично проецированию куба в двухмерное пространство.
Проекции на 2D-плоскость становятся более наглядными, меняя положение проецируемых вершин. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения внутри тессеракта, но которые иллюстрируют структуру соединения вершин, например, в следующих примерах:
Тессеракт в принципе получается путем объединения двух кубов. Схема аналогична построению куба из двух квадратов: сопоставьте две копии куба меньшей размерности и соедините соответствующие вершины. Каждый край тессеракта имеет одинаковую длину. Это представление представляет интерес при использовании тессерактов в качестве основы для топология сети связать несколько процессоров в параллельные вычисления: расстояние между двумя узлами не превышает 4, и существует множество различных путей для балансировки веса.
Параллельные проекции в 3 измерения

В клеточный параллельно проекция тессеракта в трехмерное пространство имеет кубический конверт. Ближайшие и самые дальние ячейки проецируются на куб, а остальные шесть ячеек проецируются на шесть квадратных граней куба.
В лицом вперед параллельная проекция тессеракта в трехмерное пространство имеет кубовидный конверт. Две пары ячеек выступают на верхнюю и нижнюю половины этой оболочки, а четыре оставшиеся ячейки выступают на боковые грани.
В край вперед параллельная проекция тессеракта в трехмерное пространство имеет оболочку в виде шестиугольная призма. Шесть ячеек проецируются на ромбические призмы, которые располагаются в шестиугольной призме аналогично тому, как грани трехмерного куба проецируются на шесть ромбов в шестиугольной оболочке при проекции в первую вершину. Две оставшиеся ячейки выступают на основания призм.

В вершина первая параллельная проекция тессеракта в трехмерное пространство имеет ромбический додекаэдр конверт. Две вершины тессеракта проецируются в начало координат. Есть ровно два способа рассечение ромбический додекаэдр на четыре конгруэнтных ромбоэдры, давая в общей сложности восемь возможных ромбоэдров, каждый из которых куб тессеракта. Эта проекция также имеет максимальную громкость. Один набор векторов проекции ты=(1,1,-1,-1), v=(-1,1,-1,1), ш=(1,-1,-1,1).
Как конфигурация
Этот матрица конфигурации представляет тессеракт. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем тессеракте. Недиагональные числа говорят, сколько элементов столбца находится в элементе строки или рядом с ним.[7] Например, 2 в первом столбце второй строки указывает на то, что есть 2 вершины в каждом ребре (т.е. на крайних точках); цифра 4 во втором столбце первой строки указывает на то, что 4 ребра пересекаются в каждой вершине.
Галерея
 |  Стереоскопический 3D-проекция тессеракта (параллельный вид) |
Альтернативные прогнозы
 Трехмерная проекция тессеракта, выполняющая двойное вращение около двух ортогональных плоскостей | 3D-проекция трех мозаик с гранями и без |  Перспектива с устранение скрытого тома. Красный угол - ближайший в 4D и имеет 4 кубические ячейки, соединяющиеся вокруг него. |
 В тетраэдр формирует выпуклый корпус вершинно-центрированной центральной проекции тессеракта. Показаны четыре из 8 кубических ячеек. 16-я вершина проецируется на бесконечность и четыре его края не показаны. |  Стереографическая проекция (Края проецируются на 3-сфера ) |

2D ортогональные проекции
| Самолет Кокстера | B4 | B3 / D4 / А2 | B2 / D3 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [6] | [4] |
| Самолет Кокстера | Другой | F4 | А3 |
| График |  | 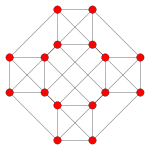 |  |
| Двугранная симметрия | [2] | [12/3] | [4] |
Радиальная равносторонняя симметрия
Длинный радиус (от центра до вершины) тессеракта равен длине его края; таким образом, его диагональ, проходящая через центр (от вершины к противоположной вершине), составляет 2 длины ребра. Только несколько униформ многогранники обладают этим свойством, включая четырехмерный тессеракт и 24-элементный, трехмерный кубооктаэдр, а двумерный шестиугольник. В частности, тессеракт - единственный гиперкуб с таким свойством.[9] Наибольший диаметр от вершины до вершины п-мерный гиперкуб единичной длины ребра равен √п, так что для квадрата это √2, для куба это √3, и только для тессеракта это √4, ровно 2 длины кромки.
Мозаика
Тессеракт, как и все гиперкубы, мозаики Евклидово пространство. Самодвойственный тессерактические соты состоящий из 4 мозаик вокруг каждой грани Schläfli символ {4,3,3,4}. Следовательно, тессеракт имеет двугранный угол 90 °.[10]
Радиальная равносторонняя симметрия тессеракта делает его мозаику идеальной. уникальная регулярная объемно-центрированная кубическая решетка сфер одинакового размера в любом количестве измерений.
Сам тессеракт можно разложить на более мелкие многогранники. Например, это может быть триангулированный в 4-х мерный симплексы которые разделяют свои вершины с тессерактом. Известно, что существует 92487256 таких триангуляций.[11] и что наименьшее количество 4-мерных симплексов в любом из них равно 16.[12]
Связанный сложный многоугольник
| Ортогональный | Перспектива |
|---|---|
 |  |
| 4{4}2, с 16 вершинами и 8 4-гранями, причем 8 4-ребер показаны здесь как 4 красных и 4 синих квадрата. | |
В правильный комплексный многогранник 4{4}2, ![]()
![]()
![]() , в имеет реальное представление в виде тессеракта или 4-4 дуопризма в 4-х мерном пространстве. 4{4}2 имеет 16 вершин и 8 4-ребер. Его симметрия 4[4]2, порядок 32. Он также имеет конструкцию более низкой симметрии,
, в имеет реальное представление в виде тессеракта или 4-4 дуопризма в 4-х мерном пространстве. 4{4}2 имеет 16 вершин и 8 4-ребер. Его симметрия 4[4]2, порядок 32. Он также имеет конструкцию более низкой симметрии, ![]()
![]()
![]() , или же 4{}×4{}, с симметрией 4[2]4, порядок 16. Это симметрия, если красные и синие 4-ребра считаются разными.[13]
, или же 4{}×4{}, с симметрией 4[2]4, порядок 16. Это симметрия, если красные и синие 4-ребра считаются разными.[13]
Связанные многогранники и соты
Как униформа дуопризма, тессеракт существует в последовательность однородных дуопризм: {п}×{4}.
Обычный тессеракт вместе с 16 ячеек, существует в наборе из 15 равномерные 4-многогранники с одинаковой симметрией. Тессеракт {4,3,3} существует в последовательность правильных 4-многогранников и сот, {п, 3,3} с четырехгранный фигуры вершин, {3,3}. Тессеракт также находится в последовательность правильных 4-многогранников и сот, {4,3,п} с кубический клетки.
В популярной культуре
С момента их открытия четырехмерные гиперкубы были популярной темой в искусстве, архитектуре и научной фантастике. Известные примеры включают:
- "И он построил кривой дом ", Роберт Хайнлайн Научно-фантастический рассказ 1940 года о здании в форме четырехмерного гиперкуба.[14] Это и Мартин Гарднер "Беспристрастный профессор", опубликованные в 1946 году, являются одними из первых произведений научной фантастики, знакомящих читателей с Группа Мебиуса, то Бутылка Клейна, и гиперкуб (тессеракт).
- Распятие (Corpus Hypercubus), картина маслом 1954 года Сальвадора Дали, изображающая четырехмерный гиперкуб, развернутый в трехмерный Латинский крест.[15]
- В Grande Arche, памятник и здание недалеко от Парижа, Франция, построенное в 1989 году. По словам инженера памятника, Эрик Райцель Большая арка была спроектирована так, чтобы напоминать проекцию гиперкуба.[16]
- Фес, видеоигра, в которой вы играете персонажем, который может видеть за пределами двух измерений, которые видят другие персонажи, и должен использовать эту способность для решения платформерных головоломок. Включает «Точку», тессеракт, который помогает вам ориентироваться в мире и рассказывает, как использовать способности, соответствующие теме видения за пределами человеческого восприятия известного пространственного пространства.[17]
Слово тессеракт позже был принят для множества других применений в популярной культуре, в том числе в качестве сюжетного устройства в произведениях научной фантастики, часто практически без связи с четырехмерным гиперкубом в этой статье. Видеть Тессеракт (значения).
Смотрите также
Примечания
- ^ «Тессеракт - 4-х мерный куб». www.cut-the-knot.org. Получено 2020-11-09.
- ^ Матила Гика, Геометрия искусства и жизни (1977), стр.68
- ^ Этот термин также может означать поликуб из четырех кубиков
- ^ Элте, Э. Л. (1912). Полурегулярные многогранники гиперпространств. Гронинген: Университет Гронингена. ISBN 1-4181-7968-X.
- ^ Кокстер 1973, стр. 122–123, §7.2. Иллюстрация Рис 7.2C.
- ^ "Домашняя страница: Оксфордский словарь английского языка". Oed.com. Получено 21 января 2018.
- ^ Кокстер 1973, п. 12, §1.8 Конфигурации.
- ^ «Раскладывающийся 8-элементный». Unfolding.apperceptual.com. Получено 21 января 2018.
- ^ Строго говоря, гиперкубы 0 измерений (точка) и 1 измерения (отрезок линии) также радиально равносторонние.
- ^ Кокстер 1973, п. 293.
- ^ Пурнин, Лайонел (2013), «Флип-граф четырехмерного куба связан», Дискретная и вычислительная геометрия, 49 (3): 511–530, arXiv:1201.6543, Дои:10.1007 / s00454-013-9488-у, МИСТЕР 3038527, S2CID 30946324
- ^ Коттл, Ричард В. (1982), «Минимальная триангуляция 4-куба», Дискретная математика, 40: 25–29, Дои:10.1016 / 0012-365X (82) 90185-6, МИСТЕР 0676709
- ^ Кокстер, Х. С. М., Регулярные сложные многогранники, второе издание, Cambridge University Press, (1991).
- ^ Фаулер, Дэвид (2010), «Математика в научной фантастике: математика как научная фантастика», Мировая литература сегодня, 84 (3): 48–52, JSTOR 27871086
- ^ Кемп, Мартин (1 января 1998 г.), "Размеры Дали", Природа, 391 (27): 27, Bibcode:1998Натура.391 ... 27К, Дои:10.1038/34063, S2CID 5317132
- ^ Урсын, Анна (2016), «Визуализация знаний и визуальная грамотность в естественно-научном образовании», Визуализация знаний и визуальная грамотность в естественнонаучном образовании, Справочник по информатике, стр. 91, ISBN 9781522504818
- ^ «Точка (персонаж) - гигантская бомба». Гигантская бомба. Получено 21 января 2018.
Рекомендации
- Кокстер, H.S.M. (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр. стр.122 –123.CS1 maint: ref = harv (связь)
- Ф. Артур Шерк, Питер МакМаллен, Энтони К. Томпсон, Азия Ивич Вайс (1995) Калейдоскопы: Избранные произведения Х.С.М. Coxeter, Публикация Wiley-Interscience ISBN 978-0-471-01003-6 [1]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, Mathematische Zeitschrift 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 26. с. 409: Hemicubes: 1n1)
- Т. Госсет (1900) О регулярных и полурегулярных фигурах в пространстве n измерений, Посланник математики, Macmillan.
- Т. Проктор Холл (1893) «Проекция четырехмерной фигуры на трехуровневую», Американский журнал математики 15:179–89.
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. (1966)
- Виктор Шлегель (1886) Ueber Projectionmodelle der regelmässigen vier-Dimensalen Körper, Варен.
внешняя ссылка
- Вайсштейн, Эрик В. «Тессеракт». MathWorld.
- Клитцинг, Ричард. "4D однородные многогранники (полихоры) x4o3o3o - tes".
- Тессеракт Изображения с трассировкой лучей с устранением скрытых поверхностей. На этом сайте представлено хорошее описание методов визуализации четырехмерных тел.
- Der 8-Zeller (8-элементный) Регулярные многогранники Марко Мёллера в ℝ4 (Немецкий)
- WikiChoron: Тессеракт
- HyperSolids это программа с открытым исходным кодом для Apple Macintosh (Mac OS X и выше), который генерирует пять правильных тел трехмерного пространства и шесть регулярных гиперсолидиков четырехмерного пространства.
- Гиперкуб 98 А Windows программа, отображающая анимированные гиперкубы, Руди Ракер
- Домашняя страница Кена Перлина Способ визуализации гиперкубов с помощью Кен Перлин
- Некоторые заметки о четвертом измерении включает анимированные руководства по нескольким различным аспектам тессеракта Давид П. Червоне
- Анимация тессеракта с устранением скрытого объема






