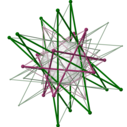
Многоугольник Петри - Petrie polygon
В геометрия, а Многоугольник Петри для правильный многогранник из п размеры - это наклонный многоугольник в котором каждый (п - 1) последовательный стороны (но нет п) принадлежит одному из грани. В Многоугольник Петри из правильный многоугольник - это сам правильный многоугольник; что из правильный многогранник это наклонный многоугольник так что каждые два последовательных сторона (но не три) принадлежит одному из лица.[1] Полигоны Петри названы в честь математика Джона Флиндерса Петри.
Для каждого правильного многогранника существует ортогональная проекция на плоскость так, что один многоугольник Петри становится правильный многоугольник с остальной частью проекции к нему. Рассматриваемый самолет является Самолет Кокстера из группа симметрии многоугольника, и количество сторон, час, является Число Кокстера из Группа Коксетера. Эти многоугольники и спроецированные графы полезны для визуализации симметричной структуры многомерных правильных многогранников.
Полигоны Петри могут быть определены более широко для любого встроенный граф. Они образуют грани другого вложения того же графа, обычно на другой поверхности, называемой Петри двойной.[2]
История
Джон Флиндерс Петри (1907–1972) был единственным сыном египтолог Флиндерс Петри. Он родился в 1907 году и, будучи школьником, показал замечательные математические способности. В периоды интенсивной концентрации он мог отвечать на вопросы о сложных четырехмерных объектах с помощью визуализация их.
Он первым отметил важность правильных косых многоугольников, которые появляются на поверхности правильных многогранников и высших многогранников. Кокстер объяснил в 1937 году, как он и Петри начали расширять классическую тему правильных многогранников:
- Однажды в 1926 году Дж. Ф. Петри с большим волнением рассказал мне, что он открыл два новых правильных многогранника; бесконечно, но без ложных вершин. Когда мое недоверие начало утихать, он описал мне их: один состоит из квадратов, по шесть в каждой вершине, и один, состоящий из шестиугольников, по четыре в каждой вершине.[3]
В 1938 году Петри сотрудничал с Кокстером, Патрик дю Валь, и Х. Flather производить Пятьдесят девять икосаэдров для публикации.[4]Понимая геометрические возможности косых многоугольников, используемых Петри, Кокстер назвал их в честь своего друга, когда писал: Правильные многогранники.
Позднее идея полигонов Петри была распространена на полуправильные многогранники.
Многоугольники Петри правильных многогранников
В обычные дуалы, {п,q} и {q,п}, содержатся внутри одного и того же спроецированного многоугольника Петри. На изображениях двойные соединения справа можно увидеть, что их многоугольники Петри имеют прямоугольные пересечения в точках, где края касаются общих средняя сфера.
| Квадрат | Шестиугольник | Декагон | ||
|---|---|---|---|---|
 |  |  | 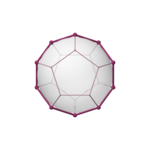 |  |
| тетраэдр {3,3} | куб {4,3} | октаэдр {3,4} | додекаэдр {5,3} | икосаэдр {3,5} |
| по краю | вершинно-центрированный | сосредоточенный на лице | сосредоточенный на лице | вершинно-центрированный |
| V:(4,0) | V:(6,2) | V:(6,0) | V:(10,10,0) | V:(10,2) |
Многоугольники Петри являются внешней стороной этих ортогональных проекций. | ||||
Многоугольники Петри Многогранники Кеплера – Пуансо находятся шестиугольники {6} и декаграммы {10/3}.
| Шестиугольник | Декаграмма | ||
|---|---|---|---|
 |  |  |  |
| gD {5,5/2} | sD {5,5/2} | gI {3,5/2} | GSD {5/2,3} |
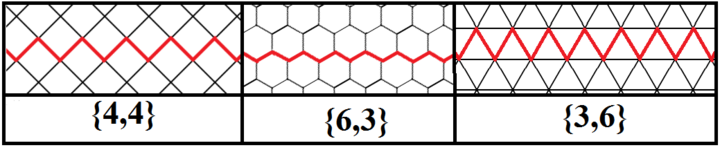
Бесконечные правильные косые многоугольники (апейрогон ) также можно определить как многоугольники Петри правильных мозаик, имеющих углы в 90, 120 и 60 градусов их квадратных, шестиугольных и треугольных граней соответственно.
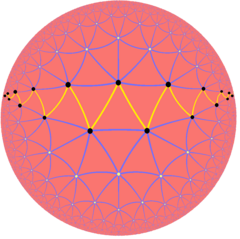
Бесконечные правильные косые многоугольники также существуют как многоугольники Петри регулярных гиперболических мозаик, например Треугольная мозаика порядка 7, {3,7}:
Многоугольник Петри правильной полихоры (4-многогранники)
Многоугольник Петри для правильной полихоры {п, q ,р} также можно определить.
 {3,3,3} 5-элементный 5 сторон V:(5,0) | 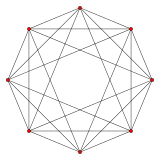 {3,3,4} 16 ячеек 8 сторон V:(8,0) |  {4,3,3} тессеракт 8 сторон V:(8,8,0) |
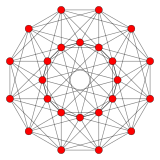 {3,4,3} 24-элементный 12 сторон V:(12,6,6,0) |  {5,3,3} 120 ячеек 30 сторон V:((30,60)3,603,30,60,0) | 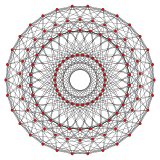 {3,3,5} 600 ячеек 30 сторон V: (30,30,30,30,0) |
Многоугольные проекции Петри правильных и однородных многогранников
Проекции многоугольника Петри полезны для визуализации многогранников размерности четыре и выше.
Гиперкубы
А гиперкуб измерения п имеет многоугольник Петри размером 2п, что также является числом его грани.
Итак, каждый из (п−1) -кубов, образующих его поверхность имеет п−1 сторона многоугольника Петри среди его ребер.
| Гиперкубы | ||
|---|---|---|
Петри из 1 кубика Digon выглядит идентично 1-кубу. Но у 1-куба одно ребро, а у двуугольника - два.
(За п= 1 первая и вторая половина - два различных, но совпадающих ребра двуугольника.)
| ||
| Квадрат | Куб | Тессеракт |
 | 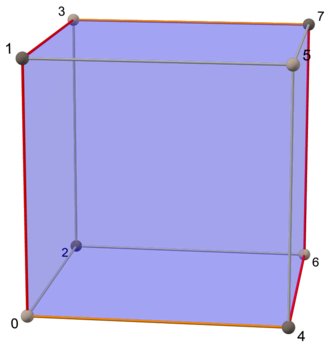 | 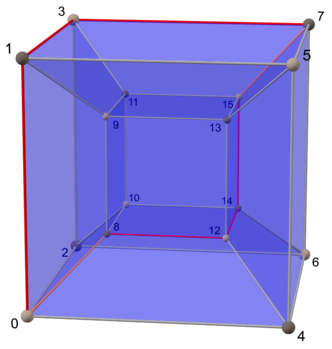 |
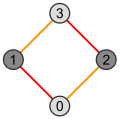 | 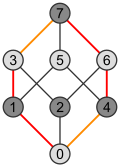 | 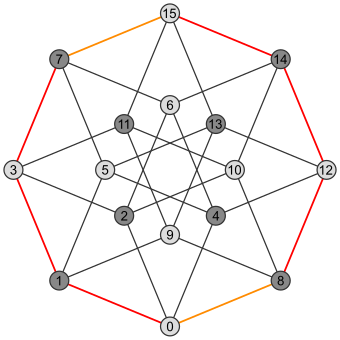 |
Неприводимые семейства многогранников
В этой таблице представлены полигональные проекции Петри трех правильных семейств (симплекс, гиперкуб, ортоплекс ), а исключительная группа Ли Eп которые порождают полуправильные и однородные многогранники для размерностей от 4 до 8.
Эта статья не цитировать любой источники. (Май 2019) (Узнайте, как и когда удалить этот шаблон сообщения) |
Примечания
- ^ Калейдоскопы: Избранные произведения Х. С. М. Кокстерапод редакцией Ф. Артура Шерка, Питер МакМаллен, Энтони С. Томпсон, Азия Ивич Вайс, публикация Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1] (Определение: статья 13, Дискретные группы, порожденные отражениями, 1933, стр. 161)
- ^ Горини, Екатерина А. (2000), Геометрия в действии, Примечания МАА, 53, Cambridge University Press, стр. 181, ISBN 9780883851647
- ^ H.S.M. Кокстер (1937) "Правильный косой многогранник в трех и четырех измерениях и их топологические аналоги", Труды Лондонского математического общества (2) 43: 33-62
- ^ Х. С. М. Кокстер, Патрик дю Валь, H.T. Флатер, Дж. Ф. Петри (1938) Пятьдесят девять Икосаэдров, Университет Торонто этюды, математическая серия 6: 1–26
- ^ http://cms.math.ca/openaccess/cjm/v10/cjm1958v10.0220-0221.pdf
Рекомендации
- Coxeter, Х. С. М. (1947, 63, 73) Правильные многогранники, 3-е изд. Нью-Йорк: Дувр, 1973 г. (раздел 2.6 Полигоны Петри стр. 24–25 и Глава 12, стр. 213–235, Обобщенный многоугольник Петри )
- Кокстер, H.S.M. (1974) Правильные сложные многогранники. Раздел 4.3 Флаги и ортосхемы, Раздел 11.3 Многоугольники Петри
- Болл, У. У. Р. и Х. С. М. Кокстер (1987) Математические развлечения и эссе, 13-е изд. Нью-Йорк: Дувр. (стр.135)
- Кокстер, Х. С. М. (1999) Красота геометрии: двенадцать эссе, Dover Publications LCCN 99-35678
- Питер МакМаллен, Эгон Шульте (2002) Абстрактные правильные многогранники, Издательство Кембриджского университета. ISBN 0-521-81496-0
- Стейнберг, Роберт,О ЧИСЛЕ СТОРОН ПЕТРИ-ПОЛИГОНА
Смотрите также
Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Семья | Ап | Bп | я2(п) / Dп | E6 / E7 / E8 / F4 / грамм2 | ЧАСп | |||||||
| Правильный многоугольник | Треугольник | Квадрат | п-угольник | Шестиугольник | Пентагон | |||||||
| Равномерный многогранник | Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | ||||||||
| Равномерный 4-многогранник | 5-элементный | 16 ячеек • Тессеракт | Demitesseract | 24-элементный | 120 ячеек • 600 ячеек | |||||||
| Равномерный 5-многогранник | 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | |||||||||
| Равномерный 6-многогранник | 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | ||||||||
| Равномерный 7-многогранник | 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | ||||||||
| Равномерный 8-многогранник | 8-симплекс | 8-ортоплекс • 8-куб | 8-полукруглый | 142 • 241 • 421 | ||||||||
| Равномерный 9-многогранник | 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | |||||||||
| Равномерный 10-многогранник | 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | |||||||||
| Униформа п-многогранник | п-симплекс | п-ортоплекс • п-куб | п-полукуб | 1k2 • 2k1 • k21 | п-пятиугольный многогранник | |||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||
внешняя ссылка
- Вайсштейн, Эрик В. «Полигон Петри». MathWorld.
- Вайсштейн, Эрик В. «Графики гиперкуба». MathWorld.
- Вайсштейн, Эрик В. "Графы кросс-многогранников". MathWorld.
- Вайсштейн, Эрик В. «24-элементный график». MathWorld.
- Вайсштейн, Эрик В. «120-ячеечный граф». MathWorld.
- Вайсштейн, Эрик В. «Граф на 600 ячеек». MathWorld.
- Вайсштейн, Эрик В. "График Госсета 3_21". MathWorld.