Двугранный угол - Dihedral angle

Угол между двумя плоскостями (α, β, зеленый) в третьей плоскости (розовой), которая пересекает линию пересечения под прямым углом.

А двугранный угол - угол между двумя пересекающимися плоскостями. В химия, это угол между плоскостями через два набора из трех атомов, имеющих два общих атома. В сплошная геометрия, он определяется как союз из линия и два полупланы которые имеют эту строку как общую край. В высшие измерения, двугранный угол представляет собой угол между двумя гиперплоскости.^[1]Говорят, что плоскости летательного аппарата расположены под положительным двугранным углом, когда как правый, так и левый основные плоскости наклонены вверх к боковой оси. Когда они наклонены вниз, говорят, что они находятся под отрицательным двугранным углом.

Математический фон

Когда две пересекающиеся плоскости описываются в терминах Декартовы координаты двумя уравнениями

{ displaystyle a_ {1} x + b_ {1} y + c_ {1} z + d_ {1} = 0}

{ displaystyle a_ {2} x + b_ {2} y + c_ {2} z + d_ {2} = 0}

двугранный угол, ${ displaystyle varphi}$ между ними определяется:

{ displaystyle cos varphi = { frac { left vert a_ {1} a_ {2} + b_ {1} b_ {2} + c_ {1} c_ {2} right vert} {{ sqrt {a_ {1} ^ {2} + b_ {1} ^ {2} + c_ {1} ^ {2}}} { sqrt {a_ {2} ^ {2} + b_ {2} ^ {2 } + c_ {2} ^ {2}}}}}}

и удовлетворяет ${ displaystyle 0 leq varphi leq pi / 2.}$

В качестве альтернативы, если $п А$ и $п B$ находятся нормальный вектор к самолетам, есть

{ displaystyle cos varphi = { frac { left vert mathbf {n} _ { mathrm {A}} cdot mathbf {n} _ { mathrm {B}} right vert} { | mathbf {n} _ { mathrm {A}} || mathbf {n} _ { mathrm {B}} |}}}

куда $п А \cdot п B$ это скалярное произведение векторов и $| п А | | п B |$ - произведение их длины.^[2]

Абсолютное значение требуется в приведенных выше формулах, поскольку плоскости не меняются при изменении всех знаков коэффициентов в одном уравнении или при замене одного вектора нормали его противоположным.

Однако абсолютных значений можно и следует избегать при рассмотрении двугранного угла двух полуплоскости границы которого совпадают. В этом случае полуплоскости можно описать точкой $п$ их пересечения, и три вектора $б 0$ , $б 1$ и $б 2$ такой, что $п + б 0$ , $п + б 1$ и $п + б 2$ принадлежат соответственно линии пересечения, первой полуплоскости и второй полуплоскости. В двугранный угол этих двух полуплоскостей определяется

{ displaystyle cos varphi = { frac {( mathbf {b} _ {0} times mathbf {b} _ {1}) cdot ( mathbf {b} _ {0} times mathbf {b} _ {2})} {| mathbf {b} _ {0} times mathbf {b} _ {1} || mathbf {b} _ {0} times mathbf {b} _ {2} |}}}

,

и удовлетворяет ${ displaystyle 0 leq varphi < pi.}$

В физике полимеров

В некоторых научных областях, таких как физика полимеров можно рассматривать цепочку точек и связей между последовательными точками. Если точки последовательно пронумерованы и расположены на позициях $р 1$ , $р 2$ , $р 3$ и т. д. векторы облигаций определяются как $ты 1$ = $р 2$ - $р 1$ , $ты 2$ = $р 3$ - $р 2$ , и $ты я$ = $р я + 1$ - $р я$ , в более общем смысле.^[3] Это случай кинематические цепи или же аминокислоты в структура белка. В этих случаях часто интересуют плоскости, определяемые тремя последовательными точками, и двугранный угол между двумя последовательными такими плоскостями. Если ориентация была выбрана для всей цепочки, каждая пара последовательных точек определяет вектор, и сумма всех этих векторов $ты я$ вектор, указывающий от начала до конца цепочки. Если $ты 1$ , $ты 2$ и $ты 3$ три последовательных таких вектора, у одного ситуация аналогична предыдущему случаю, за исключением того, что пересечение плоскостей ориентировано. Это позволяет определить двугранный угол, принадлежащий интервалу $(- π, π]$ . Этот двугранный угол определяется формулой^[4]

{ displaystyle { begin {align} cos varphi & = { frac {( mathbf {u} _ {1} times mathbf {u} _ {2}) cdot ( mathbf {u} _ {2} times mathbf {u} _ {3})} {| mathbf {u} _ {1} times mathbf {u} _ {2} | , | mathbf {u} _ {2 } times mathbf {u} _ {3} |}} sin varphi & = { frac { mathbf {u} _ {2} cdot (( mathbf {u} _ {1} раз mathbf {u} _ {2}) times ( mathbf {u} _ {2} times mathbf {u} _ {3}))} {| mathbf {u} _ {2} | , | mathbf {u} _ {1} times mathbf {u} _ {2} | , | mathbf {u} _ {2} times mathbf {u} _ {3} |}}, конец {выровнено}}}

или, используя функцию atan2,

{ displaystyle varphi = operatorname {atan2} ( mathbf {u} _ {2} cdot (( mathbf {u} _ {1} times mathbf {u} _ {2}) times ( mathbf {u} _ {2} times mathbf {u} _ {3})), | mathbf {u} _ {2} | , ( mathbf {u} _ {1} times mathbf { u} _ {2}) cdot ( mathbf {u} _ {2} times mathbf {u} _ {3})).}

Этот двугранный угол не зависит от ориентации цепочки (порядка, в котором рассматриваются точки). Фактически, изменение этого порядка заключается в замене каждого вектора его противоположным вектором и замене индексов 1 и 3. Обе операции не изменяют косинус и меняют знак синуса. Таким образом, вместе они не меняют угол.

Более простая формула для того же двугранного угла следующая (доказательство приводится ниже)

{ displaystyle { begin {align} cos varphi & = { frac {( mathbf {u} _ {1} times mathbf {u} _ {2}) cdot ( mathbf {u} _ {2} times mathbf {u} _ {3})} {| mathbf {u} _ {1} times mathbf {u} _ {2} | , | mathbf {u} _ {2 } times mathbf {u} _ {3} |}} sin varphi & = { frac {| mathbf {u} _ {2} | , mathbf {u} _ {1} cdot ( mathbf {u} _ {2} times mathbf {u} _ {3})} {| mathbf {u} _ {1} times mathbf {u} _ {2} | , | mathbf {u} _ {2} times mathbf {u} _ {3} |}}, end {align}}}

или эквивалентно,

{ displaystyle varphi = operatorname {atan2} (| mathbf {u} _ {2} | , mathbf {u} _ {1} cdot ( mathbf {u} _ {2} times mathbf {u} _ {3}), ( mathbf {u} _ {1} times mathbf {u} _ {2}) cdot ( mathbf {u} _ {2} times mathbf {u} _ {3})).}

Это можно вывести из предыдущих формул, используя вектор четырехкратное произведение формула, и тот факт, что скалярное тройное произведение равен нулю, если он содержит дважды одинаковый вектор:

{ displaystyle ( mathbf {u} _ {1} times mathbf {u} _ {2}) times ( mathbf {u} _ {2} times mathbf {u} _ {3}) = [( mathbf {u} _ {2} times mathbf {u} _ {3}) cdot mathbf {u} _ {1}] mathbf {u} _ {2} - [( mathbf { u} _ {2} times mathbf {u} _ {3}) cdot mathbf {u} _ {2}] mathbf {u} _ {1} = [( mathbf {u} _ {2 } times mathbf {u} _ {3}) cdot mathbf {u} _ {1}] mathbf {u} _ {2}}

Особые случаи ${ displaystyle varphi = pi}$ , ${ displaystyle varphi = + pi / 3}$ и ${ displaystyle varphi = - pi / 3}$ , которые называются транс, бестактный⁺, и бестактный⁻ конформации.

В стереохимии


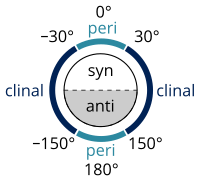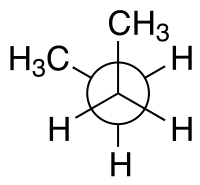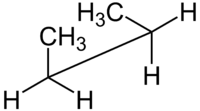Имена конфигураций по двугранному углу	син н-Бутан Проекция Ньюмана	син н-Бутан проекция козлы

Диаграмма свободной энергии п-бутан как функция двугранного угла.

В стереохимия, а угол кручения определяется как частный пример двугранного угла, описывающего геометрическое соотношение двух частей молекулы, соединенных химическая связь.^[5]^[6] Каждый набор из трех неколлинеарных атомов молекула определяет плоскость. Когда две такие плоскости пересекаются (т.е. набор из четырех последовательно связанных атомов), угол между ними составляет двугранный угол. Двугранные углы используются для определения молекулярная конформация.^[7] Стереохимический устройства, соответствующие углам от 0 ° до ± 90 °, называются син (s), соответствующие углам от ± 90 ° до 180 ° анти (а). Точно так же расположения, соответствующие углам от 30 ° до 150 ° или от -30 ° до -150 °, называются клинальный (c) и от 0 ° до ± 30 ° или от ± 150 ° до 180 ° называются перипланарный (п).

Эти два типа терминов можно комбинировать, чтобы определить четыре диапазона углов; От 0 ° до ± 30 ° синпериплоскостной (sp); От 30 ° до 90 ° и от -30 ° до -90 ° синклинально (sc); От 90 ° до 150 ° и от -90 ° до -150 ° антиклиналь (ас); От ± 150 ° до 180 ° антиперипланарный (ap). Синперипланарное строение также известно как син- или же СНГ-конформация; антиперипланарный как анти или же транс; и синклинальный как бестактный или же перекос.

Например, с п-бутан две плоскости могут быть определены в терминах двух центральных атомов углерода и любого из атомов углерода метила. В син-конформация, показанная выше, с двугранным углом 60 ° менее стабильна, чем анти-конформация с двугранным углом 180 °.

Для использования макромолекул символы T, C, G⁺, ГРАММ⁻, А⁺ и А⁻ рекомендуются (ap, sp, + sc, −sc, + ac и −ac соответственно).

Белки

Изображение белок, показывая двугранные углы позвоночника

А Рамачандран сюжет (также известная как диаграмма Рамачандрана или [φ,ψ] сюжет), первоначально разработанный в 1963 г. Г. Н. Рамачандран, Ч. Рамакришнан и В. Сасисехаран,^[8] способ визуализации энергетически разрешенных областей для двугранных углов позвоночника ψ против φ из аминокислота остатки в структура белка. На рисунке справа показано определение φ и ψ двугранные углы позвоночника^[9] (называется φ и φ ′ Рамачандрана).

В белок цепочка трех двугранных углов определяется как φ (фи), ψ (psi) и ω (омега), как показано на схеме. Планарность пептидная связь обычно ограничивает ω быть 180 ° (типичный транс случай) или 0 ° (редкий СНГ дело). Расстояние между C^α атомы в транс и СНГ изомеры составляет примерно 3,8 и 2,9 Å соответственно. Подавляющее большинство пептидных связей в белках являются транс, хотя пептидная связь с азотом пролин имеет повышенную распространенность СНГ по сравнению с другими парами аминокислот.^[10]

Двугранные углы боковой цепи обозначены χ_п (чип).^[11] Они имеют тенденцию группироваться около 180 °, 60 ° и -60 °, что называется транс, грубый⁺, и бестактный⁻ конформации. На стабильность некоторых двугранных углов боковой цепи влияют значения φ и ψ.^[12] Например, существуют прямые стерические взаимодействия между Cγ боковой цепи в бестактный⁺ ротамера и основного азота следующего остатка, когда ψ около -60 °.^[13]

Преобразование двугранных углов в декартовы координаты в цепочках

Основы полимеров, особенно белков, обычно представляют в внутренние координаты; то есть список последовательных двугранных углов и длин связей. Однако некоторые виды вычислительная химия вместо этого используйте декартовы координаты. При оптимизации вычислительной структуры некоторым программам необходимо переключаться между этими представлениями во время своих итераций. Эта задача может доминировать над временем расчета. Для процессов с большим количеством итераций или с длинными цепочками это также может привести к кумулятивной численной неточности. Хотя все алгоритмы преобразования дают математически идентичные результаты, они различаются по скорости и числовой точности.^[14]^{[неосновной источник необходим ]}

Геометрия

У каждого многогранника есть двугранный угол на каждом ребре, описывающий отношения двух граней, которые имеют это ребро. Этот двугранный угол, также называемый угол лица, измеряется как внутренний угол относительно многогранника. Угол 0 ° означает, что векторы нормалей грани равны антипараллельный и грани накладываются друг на друга, что означает, что это часть выродиться многогранник. Угол 180 ° означает, что грани параллельны, как в черепица. На вогнутых частях многогранника существует угол больше 180 °.

Каждый двугранный угол в реберно-транзитивный многогранник имеет такое же значение. Это включает 5 Платоновы тела, 13 Каталонские твердые вещества, 4 Многогранники Кеплера – Пуансо, два квазирегулярных тела и два квазирегулярных дуальных тела.

Для трех граней многогранника, которые встречаются в общей вершине P и имеют ребра AP, BP и CP, косинус двугранного угла между гранями, содержащими APC и BPC, равен:^[15]

{ displaystyle cos varphi = { frac { cos ( angle mathrm {APB}) - cos ( angle mathrm {APC}) cos ( angle mathrm {BPC})} { sin ( angle mathrm {APC}) sin ( angle mathrm {BPC})}}}

Смотрите также

Атропоизомер

внешняя ссылка

Двугранный угол в деревообработке на Tips.FM
Анализ 5 правильных многогранников дает пошаговый вывод этих точных значений.

[1] Ольшевский, Георгий. "Двугранный угол". Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.

[2] «Угол между двумя плоскостями». TutorVista.com. Получено 2018-07-06.

[kroger-3] Крегер, Мартин (2005). Модели для полимерных и анизотропных жидкостей. Springer. ISBN 3540262105.

[4] Блондель, Арно; Карплюс, Мартин (7 декабря 1998 г.). «Новая формулировка производных от торсионных углов и несобственных торсионных углов в молекулярной механике: устранение сингулярностей». Журнал вычислительной химии. 17 (9): 1132–1141. Дои:10.1002 / (SICI) 1096-987X (19960715) 17: 9 <1132 :: AID-JCC5> 3.0.CO; 2-T.

[5] ИЮПАК, Сборник химической терминологии, 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "Угол кручения ". Дои:10.1351 / goldbook.T06406

[6] ИЮПАК, Сборник химической терминологии, 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "Двугранный угол ". Дои:10.1351 / goldbook.D01730

[dougherty-7] Анслин, Эрик; Деннис Догерти (2006). Современная физико-органическая химия. Университетская наука. п. 95. ISBN 978-1891389313.

[8] Рамачандран, Г. Н .; Рамакришнан, С .; Сасисехаран, В. (1963). «Стереохимия конфигураций полипептидных цепей». Журнал молекулярной биологии. 7: 95–9. Дои:10.1016 / S0022-2836 (63) 80023-6. PMID 13990617.

[9] Ричардсон, Дж. С. (1981). Анатомия и систематика белковых структур. Успехи в химии белков. 34. С. 167–339. Дои:10.1016 / S0065-3233 (08) 60520-3. ISBN 9780120342341. PMID 7020376.

[10] Сингх Дж., Хэнсон Дж., Хеффернан Р., Паливал К., Ян Й., Чжоу Й. (август 2018 г.). «Обнаружение цис-изомеров пролина и непролина в структурах белка из последовательностей с использованием глубокого обучения остаточному ансамблю». Журнал химической информации и моделирования. 58 (9): 2033–2042. Дои:10.1021 / acs.jcim.8b00442. PMID 30118602.

[11] ttp://www.cryst.bbk.ac.uk/PPS95/course/3_geometry/conform.html

[12] Dunbrack, RL Jr .; Карплюс, М. (20 марта 1993 г.). «Зависимая от скелета библиотека ротамеров для белков. Применение для предсказания боковых цепей». Журнал молекулярной биологии. 230 (2): 543–74. Дои:10.1006 / jmbi.1993.1170. PMID 8464064.

[13] Данбрак, Р.Л. Младший; Карплюс, М. (май 1994 г.). «Конформационный анализ зависимых от остова ротамеров предпочтений белковых боковых цепей». Структурная биология природы. 1 (5): 334–40. Дои:10.1038 / nsb0594-334. PMID 7664040.

[NERF-14] Parsons, J .; Holmes, J. B .; Рохас, Дж. М .; Tsai, J .; Штраус, К. Э. (2005), "Практическое преобразование торсионного пространства в декартово пространство для синтеза белка in silico", Журнал вычислительной химии, 26 (10): 1063–1068, Дои:10.1002 / jcc.20237, PMID 15898109

[15] "калькулятор двугранного угла многогранник". www.had2know.com. Архивировано из оригинал 25 ноября 2015 г.. Получено 25 октября 2015.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]