Симплекс - Simplex

В геометрия, а симплекс (множественное число: симплексы или же симплексы) является обобщением понятия треугольник или же тетраэдр произвольно размеры.
Например,
- 0-симплекс - это точка,
- 1-симплекс - это отрезок,
- 2-симплекс - это треугольник,
- 3-симплекс - это тетраэдр,
- 4-симплекс - это 5-элементный.
В частности, k-суплекс это k-размерный многогранник какой выпуклый корпус своего k + 1 вершины. Более формально предположим, что k +1 балл находятся аффинно независимый, что значит находятся линейно независимый Тогда определяемый ими симплекс представляет собой набор точек
А обычный симплекс[1] симплекс, который также является правильный многогранник. Обычный п-симплекс может быть построен из регулярного (п - 1) -симплекс, соединяющий новую вершину со всеми исходными вершинами общей длиной ребра.
В стандартный симплекс или же вероятностный симплекс [2] симплекс, образованный k + 1 стандартные единичные векторы, или
В топология и комбинаторика, обычно «склеивают» симплексы, образуя симплициальный комплекс. Соответствующая комбинаторная структура называется абстрактный симплициальный комплекс, в этом контексте слово «симплекс» означает просто любой конечный набор вершин.
История
Понятие симплекса было известно Уильям Кингдон Клиффорд, который писал об этих формах в 1886 году, но назвал их «простыми границами». Анри Пуанкаре, писать о алгебраическая топология в 1900 г. назвал их «обобщенными тетраэдрами». В 1902 г. Питер Хендрик Шуте описал концепцию сначала с латинский превосходная степень симплициссимум («самый простой»), а затем с тем же латинским прилагательным в нормальной форме симплекс ("просто").[3]
В обычный симплекс семья первая из трех правильный многогранник семьи, помеченные Дональд Коксетер в качестве αп, два других - кросс-многогранник семья, помеченная как βп, а гиперкубы, помеченный как γп. Четвертая семья, мозаика n-мерного пространства бесконечным числом гиперкубов, он обозначил как δп.[4]
Элементы
Выпуклая оболочка любого непустого подмножества п +1 балл, определяющий п-симплекс называется лицо симплекса. Лица сами по себе являются симплексами. В частности, выпуклая оболочка подмножества размера м + 1 (из п + 1 определяющих точек) является м-симплекс, называемый м-лицо из п-симплекс. 0-грани (то есть сами определяющие точки как наборы размера 1) называются вершины (особая: вершина), 1-грани называются края, (п - 1) -лицы называются грани, а единственная п-лицо целое п-самого сложного. В целом количество м-faces равно биномиальный коэффициент .[5] Следовательно, количество м-лики п-simplex можно найти в столбце (м + 1) ряда (п + 1) из Треугольник Паскаля. Симплекс А это coface симплекса B если B это лицо А. Лицо и грань могут иметь разное значение при описании типов симплексов в симплициальный комплекс; видеть простой комплекс для более подробной информации.
Количество 1-граней (ребер) п-simplex - это п-го номер треугольника, количество 2-граней п-симплекс - это (п - 1) й число тетраэдра, количество 3-граней п-симплекс - это (п - 2) 5-ти элементный номер и так далее.
| Δп | Имя | Schläfli Coxeter | 0- лица (вершины) | 1- лица (края) | 2- лица | 3- лица | 4- лица | 5- лица | 6- лица | 7- лица | 8- лица | 9- лица | 10- лица | Сумма = 2п+1 − 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Δ0 | 0-симплекс (точка ) | ( ) | 1 | 1 | ||||||||||
| Δ1 | 1-симплекс (отрезок ) | { } = ( ) ∨ ( ) = 2 · ( ) | 2 | 1 | 3 | |||||||||
| Δ2 | 2-симплекс (треугольник ) | {3} = 3 · ( ) | 3 | 3 | 1 | 7 | ||||||||
| Δ3 | 3-симплекс (тетраэдр ) | {3,3} = 4 · ( ) | 4 | 6 | 4 | 1 | 15 | |||||||
| Δ4 | 4-симплекс (5-элементный ) | {33} = 5 · ( ) | 5 | 10 | 10 | 5 | 1 | 31 | ||||||
| Δ5 | 5-симплекс | {34} = 6 · ( ) | 6 | 15 | 20 | 15 | 6 | 1 | 63 | |||||
| Δ6 | 6-симплекс | {35} = 7 · ( ) | 7 | 21 | 35 | 35 | 21 | 7 | 1 | 127 | ||||
| Δ7 | 7-симплекс | {36} = 8 · ( ) | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | 255 | |||
| Δ8 | 8-симплекс | {37} = 9 · ( ) | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | 511 | ||
| Δ9 | 9-симплекс | {38} = 10 · ( ) | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | 1023 | |
| Δ10 | 10-симплекс | {39} = 11 · ( ) | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | 2047 |
С точки зрения непрофессионала, п-simplex - это простая форма (многоугольник), требующая п размеры. Рассмотрим отрезок прямой AB как «фигура» в одномерном пространстве (одномерное пространство - это линия, на которой лежит сегмент). Можно поставить новую точку C где-то в стороне. Новая форма, треугольник ABC, требует двух измерений; он не может поместиться в исходном одномерном пространстве. Треугольник - это 2-симплекс, простая форма, требующая двух измерений. Рассмотрим треугольник ABC, фигура в 2-мерном пространстве (плоскость, в которой находится треугольник). Можно поставить новую точку D где-то вне самолета. Новая форма, тетраэдр ABCD, требует трех измерений; он не может поместиться в исходном двухмерном пространстве. Тетраэдр - это 3-симплекс, простая форма, требующая трех измерений. Рассмотрим тетраэдр ABCD, фигура в трехмерном пространстве (трехмерном пространстве, в котором лежит тетраэдр). Можно поставить новую точку E где-то за пределами 3-х пространств. Новая форма ABCDE, называемый 5-элементным, требует четырех измерений и называется 4-симплексным; он не может поместиться в исходном трехмерном пространстве. (Его также нельзя легко визуализировать.) Эту идею можно обобщить, то есть добавить одну новую точку за пределами текущего занятого пространства, что требует перехода в следующее более высокое измерение, чтобы удерживать новую форму. Эту идею также можно проработать и в обратном направлении: сегмент линии, с которого мы начали, представляет собой простую форму, для которой требуется одномерное пространство; отрезок прямой - это 1-симплекс. Сам отрезок линии был сформирован, начиная с одной точки в 0-мерном пространстве (эта начальная точка является 0-симплексом) и добавляя вторую точку, что потребовало увеличения до 1-мерного пространства.
Более формально (п + 1) -симплекс может быть построен как оператор соединения (∨) п-симплекс и точка, (). An (м + п + 1) -симплекс можно построить как объединение м-простой и п-симплекс. Два симплекса ориентированы так, чтобы быть полностью перпендикулярными друг другу, со смещением в направлении, ортогональном им обоим. 1-симплекс - это соединение двух точек: () ∨ () = 2 · (). Общий 2-симплекс (разносторонний треугольник) - это соединение трех точек: () ∨ () ∨ (). An равнобедренный треугольник является соединением 1-симплекса и точки: {} ∨ (). An равносторонний треугольник равно 3 · () или {3}. Общий 3-симплекс - это соединение 4 точек: () ∨ () ∨ () ∨ (). 3-симплекс с зеркальной симметрией можно представить как соединение ребра и двух точек: {} ∨ () ∨ (). 3-симплекс с треугольной симметрией может быть выражен как соединение равностороннего треугольника и 1 точки: 3. () ∨ () или {3} ∨ (). А правильный тетраэдр равно 4 · () или {3,3} и так далее.
 Номера лиц в таблице выше такие же, как и в Треугольник Паскаля, без левой диагонали. |
В некоторых соглашениях[7] пустое множество определяется как (-1) -симплекс. Определение симплекса выше все еще имеет смысл, если п = -1. Это соглашение чаще встречается в приложениях к алгебраической топологии (например, симплициальные гомологии ), чем изучение многогранников.
Симметричные графы регулярных симплексов
Эти Полигоны Петри (косоортогональные проекции) показывают все вершины правильного симплекса на окружности и все пары вершин, соединенные ребрами.
 1 | 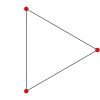 2 |  3 |  4 |  5 |
 6 |  7 |  8 |  9 |  10 |
 11 |  12 |  13 |  14 |  15 |
 16 |  17 |  18 |  19 |  20 |
Стандартный симплекс

В стандарт п-суплекс (или же единица измерения п-суплекс) - подмножество рп+1 данный
Симплекс Δп лежит в аффинная гиперплоскость получается снятием ограничения тя ≥ 0 в приведенном выше определении.
В п + 1 вершина стандарта п-simplex точки ея ∈ рп+1, куда
- е0 = (1, 0, 0, ..., 0),
- е1 = (0, 1, 0, ..., 0),
- еп = (0, 0, 0, ..., 1).
Есть каноническая карта из стандартной п-просто к произвольному п-симплекс с вершинами (v0, ..., vп) предоставлено
Коэффициенты тя называются барицентрические координаты точки в п-симплекс. Такой общий симплекс часто называют аффинный п-суплекс, чтобы подчеркнуть, что каноническое отображение является аффинное преобразование. Его также иногда называют ориентированный аффинный п-суплекс чтобы подчеркнуть, что каноническая карта может быть сохранение ориентации или реверсивный.
В общем, есть каноническая карта из стандартной -суплекс (с п вершины) на любую многогранник с п вершины, заданные тем же уравнением (изменение индексации):
Они известны как обобщенные барицентрические координаты, и выразим каждый многогранник как изображение симплекса:
Часто используемая функция из рп в интерьер стандарта -simplex - это функция softmax, или нормализованная экспоненциальная функция; это обобщает стандартная логистическая функция.
Примеры
- Δ0 это суть 1 дюйм р1.
- Δ1 - отрезок, соединяющий (1,0) и (0,1) в р2.
- Δ2 это равносторонний треугольник с вершинами (1,0,0), (0,1,0) и (0,0,1) в р3.
- Δ3 это правильный тетраэдр с вершинами (1,0,0,0), (0,1,0,0), (0,0,1,0) и (0,0,0,1) в р4.
Увеличение координат
Альтернативная система координат задается взятием неопределенная сумма:
Это дает альтернативное представление порядок, а именно как неубывающая п-кортежи от 0 до 1:
Геометрически это п-мерное подмножество (максимальная размерность, коразмерность 0), а не (коразмерность 1). Грани, которые на стандартном симплексе соответствуют нулю одной координаты, здесь соответствуют равным последовательным координатам, в то время как интерьер соответствует неравенствам, становящимся строгий (возрастающие последовательности).
Ключевым различием между этими представлениями является поведение при перестановке координат - стандартный симплекс стабилизируется перестановкой координат, в то время как перестановка элементов «упорядоченного симплекса» не оставляет его инвариантным, поскольку перестановка упорядоченной последовательности обычно делает его неупорядоченным. Действительно, упорядоченный симплекс является (замкнутым) фундаментальная область для действия симметрической группы на п-куб, означающий, что орбита упорядоченного симплекса под п! элементы симметрической группы делят п-куб в в основном непересекающиеся симплексы (непересекающиеся, за исключением границ), показывая, что этот симплекс имеет объем В качестве альтернативы, объем может быть вычислен с помощью повторного интеграла, последовательные подынтегральные выражения которого равны
Еще одним свойством этого представления является то, что он использует порядок, но не сложение, и, таким образом, может быть определен в любом измерении по любому упорядоченному набору и, например, может использоваться для определения бесконечномерного симплекса без проблем сходимости сумм.
Проекция на стандартный симплекс
Особенно в численных приложениях теория вероятности а проекция на стандартный симплекс. Данный с возможно отрицательными записями ближайшая точка на симплексе имеет координаты
куда выбирается так, что
легко вычисляется путем сортировки .[8]Подход к сортировке требует сложность, которая может быть улучшена до сложность через нахождение медианы алгоритмы.[9] Проецирование на симплекс вычислительно аналогично проецированию на мяч.
Угол куба
Наконец, простой вариант - заменить «суммирование до 1» на «суммирование не более чем до 1»; это увеличивает размерность на 1, поэтому для упрощения обозначений индексация изменяется:
Это дает п-суплекс как уголок п-куб и представляет собой стандартный ортогональный симплекс. Это симплекс, используемый в симплексный метод, который базируется в начале координат и локально моделирует вершину многогранника с п грани.
Декартовы координаты для регулярного п-мерный симплекс в рп
Один из способов записать обычный п-симплекс в рп состоит в том, чтобы выбрать две точки в качестве первых двух вершин, выбрать третью точку для создания равностороннего треугольника, выбрать четвертую точку для создания правильного тетраэдра и т. д. Каждый шаг требует выполнения уравнений, которые гарантируют, что каждая вновь выбранная вершина вместе с ранее выбранными вершинами образует регулярный симплекс. Есть несколько наборов уравнений, которые можно записать и использовать для этой цели. К ним относятся равенство всех расстояний между вершинами; равенство всех расстояний от вершин до центра симплекса; тот факт, что угол, проходящий через новую вершину любыми двумя ранее выбранными вершинами, равен ; и тот факт, что угол, проходящий через центр симплекса любыми двумя вершинами, равен .
Также можно напрямую записать конкретный регулярный п-симплекс в рп которые затем можно перемещать, вращать и масштабировать по желанию. Один из способов сделать это следующий. Обозначим базисные векторы рп к е1 через еп. Начните со стандарта (п − 1)-симплекс, представляющий собой выпуклую оболочку базисных векторов. Добавив дополнительную вершину, они станут гранью обычного п-симплекс. Дополнительная вершина должна лежать на прямой, перпендикулярной барицентру стандартного симплекса, поэтому она имеет вид (α /п, ..., α /п) для некоторого действительного числа α. Поскольку квадрат расстояния между двумя базисными векторами равен 2, чтобы дополнительная вершина образовывала регулярную п-симплекс, квадрат расстояния между ним и любым из базисных векторов также должен быть 2. Это дает квадратное уравнение для α. Решение этого уравнения показывает, что есть два варианта для дополнительной вершины:
Любой из них вместе со стандартными базисными векторами дает регулярный п-симплекс.
Вышеуказанный регулярный п-simplex не центрируется по источнику. Его можно перевести в начало координат, вычитая среднее значение его вершин. При изменении масштаба можно задать единичную длину стороны. В результате получается симплекс, вершины которого:
за , и
Этот симплекс вписан в гиперсферу радиуса .
Другое изменение масштаба дает симплекс, вписанный в единичную гиперсферу. Когда это будет сделано, его вершины станут
куда , и
Длина стороны этого симплекса .
Высокосимметричный способ построения регулярного п-simplex - использовать представление циклическая группа Zп + 1 к ортогональные матрицы. Это п × п ортогональная матрица Q такой, что Qп + 1 = я - единичная матрица, но не меньшая степень Q является. Применяя степени этой матрицы к соответствующему вектору v произведет вершины регулярного п-симплекс. Для этого сначала заметим, что для любой ортогональной матрицы Q, есть выбор основы, в которой Q блочно-диагональная матрица
где каждый Qя ортогонален и либо 2 × 2 или же 1 × 1. Для того чтобы Q иметь порядок п + 1, все эти матрицы должны иметь порядок деления п + 1. Поэтому каждый Qя является либо 1 × 1 матрица, единственная запись которой 1 или если п странно, −1; или это 2 × 2 матрица формы
где каждый ωя целое число от нуля до п включительно. Достаточным условием того, что орбита точки является правильным симплексом, является то, что матрицы Qя образуют основу для нетривиальных неприводимых вещественных представлений Zп + 1, и вращаемый вектор не стабилизируется ни одним из них.
Практически для п даже это означает, что каждая матрица Qя является 2 × 2, существует равенство множеств
и для каждого Qя, записи v на которой Qя действия не равны нулю. Например, когда п = 4, одна возможная матрица
Применяя это к вектору (1, 0, 1, 0) приводит к симплексу, вершины которого
каждый из которых находится на расстоянии √5 от других. п нечетно, условие означает, что ровно один из диагональных блоков 1 × 1, равно −1, и действует при ненулевом входе v; а остальные диагональные блоки, скажем, Q1, ..., Q(п − 1) / 2, находятся 2 × 2, существует равенство множеств
и каждый диагональный блок действует на пару записей v которые не равны нулю. Так, например, когда п = 3, матрица может быть
Для вектора (1, 0, 1/√2), получившийся симплекс имеет вершины
каждый из которых находится на расстоянии 2 от других.
Геометрические свойства
Объем
В объем из п-симплекс в п-мерное пространство с вершинами (v0, ..., vп) является
где каждый столбец п × п детерминант разница между векторов представляющий две вершины.[10] Более симметричный способ записи -
Другой распространенный способ вычисления объема симплекса - через Определитель Кэли-Менгера. Он также может вычислить объем симплекса, встроенного в многомерное пространство, например, треугольник в .[11]
Без 1 /п! это формула для объема п-параллелоэдр. Это можно понять следующим образом: Предположим, что п является п-параллелотоп, построенный на основе из .Данная перестановка из , вызовите список вершин а п-path, если
(так что есть п! п-путь и не зависит от перестановки). Имеют место следующие утверждения:
Если п это единица п-гиперкуб, то объединение п-симплексы, образованные выпуклой оболочкой каждого п-path есть п, и эти симплексы конгруэнтны и попарно не перекрываются.[12] В частности, объем такого симплекса составляет
Если п - общий параллелоэдр, те же утверждения верны, за исключением того, что в размерности> 2 уже неверно, что симплексы должны быть попарно конгруэнтными; но их объемы остаются равными, потому что п-параллелотоп - это изображение единицы п-гиперкуб линейным изоморфизмом, посылающим канонический базис к . Как и раньше, это означает, что объем симплекса, исходящий от п-path:
И наоборот, учитывая п-суплекс из , можно предположить, что векторы составляют основу . Рассматривая параллелоэдр, построенный из и , видно, что предыдущая формула верна для любого симплекса.
Наконец, формула в начале этого раздела получается, если учесть, что
Из этой формулы сразу следует, что объем по стандарту п-симплекс (т.е. между исходной точкой и симплексом в рп+1) является
Объем обычного п-суплекс с единичной длиной стороны
как можно увидеть, умножив предыдущую формулу на Иксп+1, чтобы получить объем под п-симплекс как функция его вершинного расстояния Икс от начала координат, дифференцируя по Икс, в (где п-длина симплексной стороны равна 1), а нормированная по длине приращения, вдоль вектора нормали.
Двугранные углы правильного n-симплекса
Любые две (n-1) -мерные грани правильного п-мерные симплексы сами по себе регулярны (п-1)-мерные симплексы, и у них одинаковые двугранный угол из cos−1(1/п).[13][14]
В этом можно убедиться, заметив, что центр стандартного симплекса , а центры его граней - координатные перестановки . Тогда по симметрии вектор, указывающий из к перпендикулярно граням. Таким образом, векторы, нормальные к граням, являются перестановками , из которого рассчитываются двугранные углы.
Симплексы с «ортогональным углом»
«Ортогональный угол» здесь означает, что существует вершина, в которой все смежные ребра попарно ортогональны. Отсюда сразу следует, что все смежные лица попарно ортогональны. Такие симплексы являются обобщениями прямоугольных треугольников, и для них существует п-размерный вариант теорема Пифагора:
Сумма квадратов (п - 1) -мерный объем граней, примыкающих к ортогональному углу, равен квадрату (п - 1) -размерный объем фаски напротив ортогонального угла.
куда являются фасетами, попарно ортогональными друг другу, но не ортогональными , которая представляет собой грань, противоположную ортогональному углу.
Для 2-симплекса теорема является теорема Пифагора для треугольников с прямым углом и для 3-симплекса это теорема де Гуа для тетраэдра с ортогональным углом.
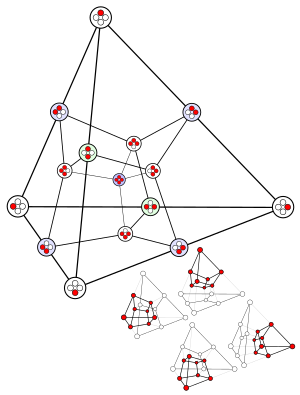
Отношение к (п + 1) -гиперкуб
В Диаграмма Хассе лицевой решетки п-симплекс изоморфен графику (п + 1)-гиперкуб ребер, причем вершины гиперкуба отображаются в каждую из п-элементы -симплекса, включая весь симплекс и нулевой многогранник как крайние точки решетки (сопоставленные с двумя противоположными вершинами на гиперкубе). Этот факт может быть использован для эффективного перечисления решетки граней симплекса, поскольку более общие алгоритмы перечисления решетки граней являются более дорогостоящими в вычислительном отношении.
В п-simplex также является вершина фигуры из (п +1) -гиперкуб. Это также грань из (п + 1)-ортоплекс.
Топология
Топологически, п-simplex есть эквивалент для п-мяч. Каждый п-simplex - это п-размерный коллектор с углами.
Вероятность
В теории вероятностей точки стандарта п-симплекс в (п + 1) -пространство образуют пространство возможных распределений вероятностей на конечном множестве, состоящем из n + 1 возможных исходов. Соответствие выглядит следующим образом: каждому распределению, описанному как упорядоченный (n + 1) -набор вероятностей, сумма которых (обязательно) равна 1, мы связываем точку симплекса, чья барицентрические координаты и есть такие вероятности. Таким образом, k-й вершине симплекса также назначается k-я вероятность (n + 1) -набора в качестве барицентрического коэффициента. Это соответствие является аффинным гомеоморфизмом.
Соединения
Поскольку все симплексы самодвойственны, они могут образовывать серию соединений;
- Два треугольника образуют гексаграмма {6/2}.
- Два тетраэдра образуют соединение двух тетраэдров или же Stella Octangula.
- Две 5-ячейки образуют соединение двух 5-ти ячеек в четырех измерениях.
Алгебраическая топология
В алгебраическая топология, симплексы используются как строительные блоки для построения интересного класса топологические пространства называется симплициальные комплексы. Эти пространства построены из симплексов, склеенных в комбинаторный мода. Симплициальные комплексы используются для определения определенного вида гомология называется симплициальные гомологии.
Конечный набор k-симплексы, встроенные в открытое подмножество из рп называется аффинный k-цепь. Симплексы в цепочке не обязательно должны быть уникальными; они могут произойти с множественность. Вместо того, чтобы использовать стандартную нотацию набора для обозначения аффинной цепочки, вместо этого стандартной практикой является использование знаков плюса для разделения каждого члена в наборе. Если у некоторых симплексов обратное ориентация, перед ними стоит знак минус. Если некоторые симплексы встречаются в наборе более одного раза, они имеют префикс с целым числом. Таким образом, аффинная цепочка принимает символическую форму суммы с целыми коэффициентами.
Обратите внимание, что каждый аспект п-симплекс является аффинным (п - 1) -симплекс, и, следовательно, граница из п-simplex является аффинным п - 1-цепочка. Таким образом, если обозначить один положительно ориентированный аффинный симплекс как
с обозначая вершины, то граница из σ это цепь
Из этого выражения и линейности граничного оператора следует, что граница границы симплекса равна нулю:
Точно так же граница границы цепи равна нулю: .
В более общем смысле симплекс (и цепь) могут быть встроены в многообразие с помощью гладкого дифференцируемого отображения . В этом случае и соглашение о суммировании для обозначения набора, и граничная операция коммутируют с встраивание. То есть,
где - целые числа, обозначающие ориентацию и множественность. Для граничного оператора , надо:
где ρ - цепь. Граничная операция коммутируется с отображением, потому что, в конце концов, цепочка определяется как набор и немного больше, а операция набора всегда коммутирует с карта операции (по определению карты).
Непрерывная карта к топологическое пространство Икс часто называют единственное число п-суплекс. (Карта обычно называется «сингулярной», если она не обладает каким-либо желаемым свойством, таким как непрерывность, и в этом случае термин предназначен для отражения того факта, что непрерывная карта не обязательно должна быть вложением.)[15]
Алгебраическая геометрия
Поскольку классическая алгебраическая геометрия позволяет говорить о полиномиальных уравнениях, но не о неравенствах, алгебраический стандартный n-симплекс обычно определяется как подмножество аффинных (п + 1) -мерное пространство, где сумма всех координат равна 1 (таким образом, исключая часть неравенства). Алгебраическое описание этого множества таково:
что равно схема -теоретическое описание с
кольцо регулярных функций на алгебраической п-симплекс (для любого кольца ).
Используя те же определения, что и для классического п-симплекс, п-просты для разных размеров п собрать в один симплициальный объект, а кольца собрать в один косимплициальный объект (в категории схем или колец, поскольку все отображения граней и вырождения полиномиальны).
Алгебраический п-симплексы используются в высших K-теория и в определении высшего Группы чау.
Приложения
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Декабрь 2009 г.) |
- В статистика, симплексы являются выборочными пространствами композиционные данные и также используются для построения графиков сумм, которые в сумме равны 1, например, пропорции субпопуляций, как в тройной сюжет.
- В промышленная статистика, симплексы возникают при постановке задачи и алгоритмическом решении. В дизайне хлеба производитель должен сочетать дрожжи, муку, воду, сахар и т. Д. смеси, имеет значение только относительное соотношение ингредиентов: для получения оптимальной хлебной смеси, если количество муки увеличено вдвое, то дрожжи должны быть удвоены. Такая задача смешения часто формулируется с нормализованными ограничениями, так что сумма неотрицательных компонентов равна единице, и в этом случае допустимая область образует симплекс. Качество хлебных смесей можно оценить с помощью методология поверхности отклика, а затем можно вычислить локальный максимум, используя нелинейное программирование метод, такой как последовательное квадратичное программирование.[16]
- В исследование операций, линейное программирование проблемы могут быть решены симплексный алгоритм из Джордж Данциг.
- В геометрический дизайн и компьютерная графика, многие методы сначала выполняют симплициальные триангуляции домена, а затем подходит интерполяция многочлены на каждый симплекс.[17]
- В химия, гидриды большинства элементов в p-блок может напоминать симплекс, если соединить каждый атом. Неон не реагирует с водородом и как таковой точка, фтор связывается с одним атомом водорода и образует отрезок прямой, кислород связи с двумя водородом в согнутый мода, напоминающая треугольник, азот реагирует на формирование тетраэдр, и углерод сформирует структура напоминая диаграмму Шлегеля из 5 клеток. Эта тенденция сохраняется для более тяжелых аналогов каждого элемента, а также при замене водорода на галоген атомы.
Смотрите также
- Геометрия Эйчисона
- Полный график
- Причинная динамическая триангуляция
- Геометрия расстояния
- Триангуляция Делоне
- Тетраэдр Хилла
- Другое регулярное п-многогранники
- Гиперсимплекс
- Многогранник
- Закон меткалфа
- Список правильных многогранников
- Ортосхема Schläfli
- Симплексный алгоритм - метод решения оптимизационных задач с неравенствами.
- Симплициальный комплекс
- Симплициальные гомологии
- Симплициальный набор
- Тернарный сюжет
- 3-сфера
Примечания
- ^ Элте, Э. (2006) [1912]. «IV. Пятимерный полуправильный многогранник». Полурегулярные многогранники гиперпространств. Саймон и Шустер. ISBN 978-1-4181-7968-7.
- ^ Бойд и Ванденберге 2004
- ^ Миллер, Джефф, «Симплекс», Самые ранние известные варианты использования некоторых слов математики, получено 2018-01-08
- ^ Кокстер 1973, pp. 120–124, §7.2.
- ^ Кокстер 1973, п. 120.
- ^ Слоан, Н. Дж. А. (ред.). «Последовательность A135278 (треугольник Паскаля с удаленным левым краем)». В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- ^ Козлов, Дмитрий, Комбинаторная алгебраическая топология, 2008, Springer-Verlag (Серия: Алгоритмы и вычисления в математике)
- ^ Юньмэй Чен; Сяоцзин Е (2011). «Проекция на симплекс». arXiv:1101.6081 [math.OC ].
- ^ MacUlan, N .; Де Паула, Г. Г. (1989). «Алгоритм поиска медианы с линейным временем для проектирования вектора на симплекс n». Письма об исследованиях операций. 8 (4): 219. Дои:10.1016/0167-6377(89)90064-3.
- ^ Вывод очень похожей формулы можно найти в Штейн, П. (1966). «Заметка об объеме симплекса». Американский математический ежемесячный журнал. 73 (3): 299–301. Дои:10.2307/2315353. JSTOR 2315353.
- ^ Колинз, Карен Д. "Детерминант Кэли-Менгера". MathWorld.
- ^ Каждый п-путь, соответствующий перестановке это образ п-дорожка аффинной изометрией, которая посылает к , и линейная часть которой совпадает к для всехя. следовательно каждые два п-трассы изометричны, как и их выпуклые оболочки; это объясняет конгруэнтность симплексов. Чтобы показать остальные утверждения, достаточно заметить, что внутренность симплекса определяется п-дорожка это набор точек , с и Следовательно, компоненты этих точек по отношению к каждому соответствующему перестановочному базису строго упорядочены в порядке убывания. Это объясняет, почему симплексы не перекрываются. Тот факт, что объединение симплексов - это целая единица п-гиперкуб также следует, заменяя строгие неравенства выше на "". Те же аргументы справедливы и для общего параллелоэдра, за исключением изометрии между симплексами.
- ^ Паркс, Гарольд Р.; Уиллс, Дин К. (октябрь 2002 г.). "Элементарный расчет двугранного угла регулярной п-Симплекс ». Американский математический ежемесячный журнал. 109 (8): 756–8. Дои:10.2307/3072403. JSTOR 3072403.
- ^ Уиллс, Гарольд Р .; Паркс, Дин К. (июнь 2009 г.). Связь комбинаторики перестановок и алгоритмов с геометрией (Кандидат наук). Государственный университет Орегона. HDL:1957/11929.
- ^ Ли, Джон М. (2006). Введение в топологические многообразия. Springer. С. 292–3. ISBN 978-0-387-22727-6.
- ^ Корнелл, Джон (2002). Эксперименты со смесями: конструкции, модели и анализ данных о смесях (третье изд.). Вайли. ISBN 0-471-07916-2.
- ^ Вондран, Гэри Л. (апрель 1998 г.). «Методы радиальной и усеченной тетраэдрической интерполяции» (PDF). Технический отчет HP. HPL-98-95: 1–32.
Рекомендации
- Рудин, Вальтер (1976). Принципы математического анализа (3-е изд.). Макгроу-Хилл. ISBN 0-07-054235-X. (См. Главу 10 для простого обзора топологических свойств.)
- Таненбаум, Эндрю С. (2003). "§2.5.3". Компьютерная сеть (4-е изд.). Прентис Холл. ISBN 0-13-066102-3.
- Деврой, Люк (1986). Генерация неоднородной случайной величины. ISBN 0-387-96305-7. Архивировано из оригинал на 2009-05-05.
- Кокстер, H.S.M. (1973). Правильные многогранники (3-е изд.). Дувр. ISBN 0-486-61480-8.CS1 maint: ref = harv (связь)
- С. 120–121, §7.2. см. рисунок 7-2А
- п. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в п размеры (п ≥ 5)
- Вайсштейн, Эрик В. «Симплекс». MathWorld.
- Бойд, Стивен; Ванденберге, Ливен (2004). Выпуклая оптимизация. Издательство Кембриджского университета. ISBN 978-1-107-39400-1. В качестве PDF
внешняя ссылка
- Ольшевский, Георгий. «Симплекс». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.













































































![{displaystyle sigma = [v_ {0}, v_ {1}, v_ {2}, ldots, v_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed6eed53d9743b30ffa309c46571dd378240938b)


![{displaystyle partial sigma = sum _ {j = 0} ^ {n} (- 1) ^ {j} [v_ {0}, ldots, v_ {j-1}, v_ {j + 1}, ldots, v_ { n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2605f2e81a832f9898a4c6e0b876b7c2f9ade919)
![{displaystyle partial ^ {2} sigma = частично слева (сумма _ {j = 0} ^ {n} (- 1) ^ {j} [v_ {0}, ldots, v_ {j-1}, v_ {j + 1}, ldots, v_ {n}] ight) = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c206798d0f7dcd17a3508ddc1e5273141c064153)








![{displaystyle Delta _ {n} (R) = имя оператора {Spec} (R [Delta ^ {n}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5fdc484c96359341ac664b837d50e4105e8ba6b)
![{displaystyle R [Delta ^ {n}]: = R [x_ {1}, ldots, x_ {n + 1}] left / left (1-сумма x_ {i} ight) ight.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5bf71c450f9887a70f5769650fc6ef7a4e95a3)

![R [Дельта ^ {n}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4963c6f429983cd870b906dc479a7564aa8965fe)
![R [Дельта ^ {ullet}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f88bc83050893b7e7c5e83e223a0f21494c3b1d)










