Курносый куб - Snub cube
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Январь 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Курносый куб | |
|---|---|
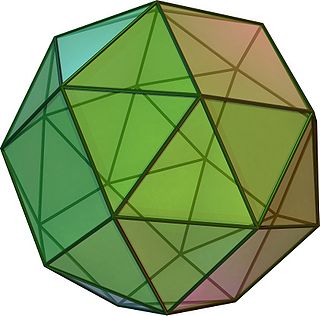 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 38, E = 60, V = 24 (χ = 2) |
| Лица по сторонам | (8+24){3}+6{4} |
| Обозначение Конвея | СК |
| Символы Шлефли | sr {4,3} или |
| ht0,1,2{4,3} | |
| Символ Wythoff | | 2 3 4 |
| Диаграмма Кокстера | |
| Группа симметрии | О, 1/2B3, [4,3]+, (432), заказ 24 |
| Группа вращения | О, [4,3]+, (432), заказ 24 |
| Двугранный угол | 3-3: 153°14′04″ (153.23°) 3-4: 142°59′00″ (142.98°) |
| Рекомендации | U12, C24, W17 |
| Характеристики | Полурегулярный выпуклый хиральный |
 Цветные лица |  3.3.3.3.4 (Фигура вершины ) |
 Пятиугольный икоситетраэдр (двойственный многогранник ) | 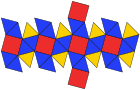 Сеть |

В геометрия, то курносый куб, или же курносый кубооктаэдр, является Архимедово твердое тело с 38 гранями: 6 квадраты и 32 равносторонние треугольники. Имеет 60 края и 24 вершины.
Это хиральный многогранник; то есть, он имеет две различные формы, которые зеркальные изображения (или "энантиоморфы ") друг друга. Объединение обеих форм является соединение двух курносых кубиков, а выпуклый корпус обоих наборов вершин является усеченный кубооктаэдр.
Кеплер впервые назвал это в латинский так как Cubus Simus в 1619 г. в его Harmonices Mundi. Х. С. М. Коксетер, отметив, что он может быть получен в равной степени из октаэдра, как и куб, назвал его курносый кубооктаэдр, с вертикальной удлиненной Символ Шлефли , и представляющий чередование из усеченный кубооктаэдр, имеющий символ Шлефли .
Размеры
Для курносого куба с длиной ребра 1 его площадь поверхности и объем равны:
где т это постоянная трибоначчи
Если исходный курносый куб имеет длину ребра 1, его двойная пятиугольный икоситетраэдр имеет длину стороны
- .
В целом объем курносого куба с длиной стороны можно найти с помощью этой формулы, используя т как константа трибоначчи выше:[1]
.
Декартовы координаты
Декартовы координаты для вершины курносого куба - все даже перестановки из
- (±1, ±1/т, ±т)
с четным числом знаков плюс, вместе со всеми нечетные перестановки с нечетным числом знаков плюс, где т ≈ 1,83929 - это постоянная трибоначчи. Если взять четные перестановки с нечетным числом знаков плюс и нечетные перестановки с четным числом знаков плюс, получится другой пренебрежительный куб - зеркальное отображение. Взяв их все вместе, получаем соединение двух курносых кубиков.
У этого курносого куба есть ребра длиной , число, удовлетворяющее уравнению
и может быть записано как
Чтобы получить курносый куб с единичной длиной ребра, разделите все указанные выше координаты на значение α приведено выше.
Ортогональные проекции

В курносый куб имеет два специальных ортогональные проекции с центром на двух типах граней: треугольники и квадраты, соответствуют букве A2 и B2 Самолеты Кокстера.
| В центре | Лицо Треугольник | Лицо Квадрат | Край |
|---|---|---|---|
| Твердый |  |  |  |
| Каркас |  |  |  |
| Проективный симметрия | [3] | [4]+ | [2] |
| Двойной |  |  |  |
Сферическая черепица
Курносый куб также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Дуги большого круга (геодезические) на сфере проецируются как дуги окружности на плоскость.
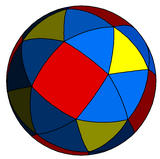 |  квадрат -центрированный |
| Ортографическая проекция | Стереографическая проекция |
|---|
Геометрические отношения
Курносый куб можно создать, взяв шесть граней куба, вытягивая их наружу чтобы они больше не касались друг друга, затем слегка повернув их центры (все по часовой стрелке или все против часовой стрелки), пока промежутки между ними не будут заполнены равносторонние треугольники.
Курносый куб также может быть получен из усеченный кубооктаэдр в процессе чередование. 24 вершины усеченного кубооктаэдра образуют многогранник, топологически эквивалентный курносому кубу; остальные 24 образуют его зеркальное отображение. В результате многогранник вершинно-транзитивный но не униформа.
«Улучшенный» курносый куб с немного меньшей квадратной гранью и немного большими треугольными гранями по сравнению с однородным курносым кубом Архимеда полезен в качестве сферический дизайн.[2]
Связанные многогранники и мозаики
Курносый куб - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | т {4,3} | г {4,3} г {31,1} | т {3,4} т {31,1} | {3,4} {31,1} | рр {4,3} s2{3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | час2{4,3} т {3,3} | с {3,4} с {31,1} |
= | = | = | ||||||||
| Двойники к однородным многогранникам | ||||||||||
| V43 | V3.82 | V (3,4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
Этот полуправильный многогранник входит в последовательность пренебрежительно многогранники и мозаики с вершинной фигурой (3.3.3.3.п) и Диаграмма Кокстера – Дынкина ![]()
![]()
![]()
![]()
![]() . Эти фигуры и их двойники имеют (п32) rotational (вращательный) симметрия, находясь в евклидовой плоскости для п = 6 и гиперболическая плоскость для любых высших п. Можно считать, что серия начинается с n = 2, причем один набор граней вырождается в дигоны.
. Эти фигуры и их двойники имеют (п32) rotational (вращательный) симметрия, находясь в евклидовой плоскости для п = 6 и гиперболическая плоскость для любых высших п. Можно считать, что серия начинается с n = 2, причем один набор граней вырождается в дигоны.
| п32 мутации симметрии курносых плиток: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия п32 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскоп цифры |  |  |  |  |  |  |  |  |
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
В курносый куб является вторым в серии курносых многогранников и мозаик с вершина фигуры 3.3.4.3.п.
| 4п2 мутации симметрии курносых плиток: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4п2 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гироскоп цифры |  |  |  |  | ||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
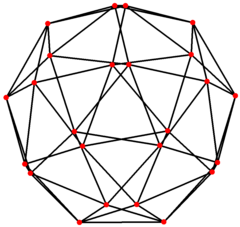
Курносый кубический граф
| Курносый кубический граф | |
|---|---|
 4-х кратная симметрия | |
| Вершины | 24 |
| Края | 60 |
| Автоморфизмы | 24 |
| Характеристики | Гамильтониан, обычный |
| Таблица графиков и параметров | |
в математический поле теория графов, а курносый кубический граф это граф вершин и ребер из курносый куб, один из Архимедовы тела. Имеет 24 вершины и 60 ребер, а это Архимедов граф.[3]
 |
Смотрите также
Рекомендации
- ^ «Плоский куб - Калькулятор геометрии». rechneronline.de. Получено 2020-05-26.
- ^ «Сферические конструкции» Р.Х. Хардин и N.J.A. Sloane
- ^ Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269
- Джаятилаке, Удая (март 2005 г.). «Вычисления на правильных многогранниках с гранями и вершинами». Математический вестник. 89 (514): 76–81.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN 0-521-55432-2.





![{ displaystyle t = { frac {1 + { sqrt [{3}] {19-3 { sqrt {33}}}} + { sqrt [{3}] {19 + 3 { sqrt {33} }}}}} {3}} примерно 1.839 , 286 , 755 , 21.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00b5dd3c4eadfd955c9c41e5b960d0f19ac5ca7e)





![{ displaystyle { begin {align} alpha & = { sqrt {{ frac {4} {3}} - { frac {16} {3 beta}} + { frac {2 beta} { 3}}}} приблизительно 1.609 , 72 beta & = { sqrt [{3}] {26 + 6 { sqrt {33}}}} end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a8d7d106963ee92fcc2a3159bcccb8de89d6bfb)















































