Обозначение орбифолда - Orbifold notation - Wikipedia

В геометрия, орбифолд обозначение (или же орбифолд подпись) - это система, изобретенная математиком Джон Конвей, для представления типов группы симметрии в двумерных пространствах постоянной кривизны. Преимущество обозначения состоит в том, что оно описывает эти группы таким образом, который указывает на многие свойства групп: в частности, оно следует Уильям Терстон в описании орбифолд полученный путем частного Евклидово пространство рассматриваемой группой.

Группы, представленные в этом обозначении, включают точечные группы на сфера ( ${ Displaystyle S ^ {2}}$ ), фризовые группы и группы обоев из Евклидова плоскость ( ${ displaystyle E ^ {2}}$ ), и их аналоги на гиперболическая плоскость ( ${ displaystyle H ^ {2}}$ ).

Определение обозначений

В группе, описываемой орбифолдной нотацией, могут встречаться следующие типы евклидовых преобразований:

отражение через линию (или плоскость)
перевод вектором
вращение конечного порядка вокруг точки
бесконечное вращение вокруг линии в 3-м пространстве
скольжение-отражение, то есть отражение с последующим переводом.

Предполагается, что все происходящие трансляции образуют дискретную подгруппу описываемых групповых симметрий.

Каждая группа обозначается в нотации орбифолда конечной строкой, составленной из следующих символов:

положительный целые числа ${ Displaystyle 1,2,3, точки}$
то бесконечность символ, ${ displaystyle infty}$
то звездочка, *
символ о (закрашенный кружок в старых документах), который называется задаваться вопросом а также ручка потому что он топологически представляет собой тор (1-ручку) замкнутую поверхность. Узоры повторяются двумя переводами.
символ ${ displaystyle times}$ (пустой кружок в старых документах), который называется чудо и представляет собой топологический перекладина где узор повторяется как зеркальное отражение, не пересекая зеркальную линию.

Строка, написанная на жирный шрифт представляет собой группу симметрий трехмерного евклидова пространства. Строка, не выделенная жирным шрифтом, представляет собой группу симметрий евклидовой плоскости, которая, как предполагается, содержит два независимых перевода.

Каждый символ соответствует отдельной трансформации:

целое число п слева от звездочки указывает вращение порядка п вокруг точка вращения
целое число п справа от звездочки обозначено преобразование порядка 2п который вращается вокруг калейдоскопической точки и отражается через линию (или плоскость)
ан ${ displaystyle times}$ указывает на скользящее отражение
символ ${ displaystyle infty}$ указывает на бесконечную симметрию вращения вокруг линии; это может произойти только для групп, выделенных жирным шрифтом. Злоупотребляя языком, мы можем сказать, что такая группа является подгруппой симметрий евклидовой плоскости только с одним независимым переводом. В фризовые группы происходят таким образом.
исключительный символ о указывает на то, что существует ровно два линейно независимых перевода.

Хорошие орбифолды

Символ орбифолда называется хороший если это не одно из следующих: п, pq, *п, *pq, за p, q≥2, и p ≠ q.

Хиральность и ахиральность

Объект хиральный если его группа симметрии не содержит отражений; иначе это называется ахиральный. Соответствующий орбифолд есть ориентируемый в киральном случае и неориентируемый в противном случае.

Эйлерова характеристика и порядок

В Эйлерова характеристика из орбифолд можно прочитать по его символу Конвея следующим образом. У каждой функции есть значение:

п без звездочки или до нее считается ${ displaystyle { frac {n-1} {n}}}$
п после звездочки считается как ${ displaystyle { frac {n-1} {2n}}}$
звездочка и ${ displaystyle times}$ считать как 1
о считается как 2.

Вычитание суммы этих значений из 2 дает эйлерову характеристику.

Если сумма значений функций равна 2, порядок бесконечен, то есть обозначение представляет группу обоев или группу фризов. Действительно, «Магическая теорема» Конвея указывает, что 17 групп обоев - это именно те, у которых сумма значений признаков равна 2. В противном случае порядок равен 2, деленному на характеристику Эйлера.

Равные группы

Следующие группы изоморфны:

1 * и * 11
22 и 221
* 22 и * 221
2 * и 2 * 1.

Это потому, что 1-кратное вращение - это «пустое» вращение.

Двумерные группы

Идеально снежинка имел бы * 6 • симметрию,	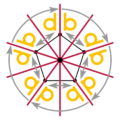В пятиугольник имеет симметрию * 5 •, все изображение со стрелками 5 •.	В Флаг Гонконга имеет 5-кратную симметрию вращения, 5 •.

В симметрия из 2D объект без трансляционной симметрии можно описать типом 3D-симметрии, добавив к объекту третье измерение, которое не добавляет и не нарушает симметрии. Например, для 2D-изображения мы можем рассматривать кусок картонной коробки с этим изображением, отображаемым на одной стороне; форма коробки должна быть такой, чтобы она не нарушала симметрию, иначе ее можно представить себе бесконечной. Таким образом, мы имеем п• и *п•. В пуля (•) добавляется к одно- и двумерным группам, чтобы подразумевать существование неподвижной точки. (В трех измерениях эти группы существуют n-кратно двуугольный орбифолд и представлены как nn и *nn.)

Аналогично 1D изображение может быть нарисовано горизонтально на картонной коробке, чтобы избежать дополнительной симметрии относительно линии изображения, например нарисовав горизонтальную полосу под изображением. Таким образом, дискретный группы симметрии в одном измерении это * •, * 1 •, ∞ • и * ∞ •.

Другой способ построения трехмерного объекта из одномерного или двухмерного объекта для описания симметрии - это использование Декартово произведение объекта и асимметричного 2D или 1D объекта соответственно.

Таблицы соответствий

Сферический

Фундаментальные области отражающих трехмерных точечных групп
(* 11), С_1v= C_s	(* 22), С_2v	(* 33), С_3в	(* 44), С_4в	(* 55), С_5в	(* 66), С_6v
Заказ 2	Заказ 4	Заказ 6	Заказ 8	Заказ 10	Заказ 12
(* 221), D_{1 час}= C_2v	(* 222), D_2ч	(* 223), D_3ч	(* 224), D_4ч	(* 225), D_5ч	(* 226), D_6ч
Заказ 4	Заказ 8	Заказ 12	Заказ 16	Заказ 20	Заказ 24
(* 332), т_d		(* 432), О_час		(* 532), я_час
Заказ 24		Заказ 48		Заказ 120

Группы сферической симметрии^[1]
Орбифолд Подпись	Coxeter	Schönflies	Герман-Моген	Заказ
Группы полиэдров
*532	[3,5]	я_час	53м	120
532	[3,5]⁺	я	532	60
*432	[3,4]	О_час	м3м	48
432	[3,4]⁺	О	432	24
*332	[3,3]	Т_d	43м	24
3*2	[3⁺,4]	Т_час	м3	24
332	[3,3]⁺	Т	23	12
Диэдральные и циклические группы: n = 3,4,5 ...
* 22n	[2, n]	D_нэ	н / ммм или 2пm2	4n
2 * п	[2⁺, 2н]	D_nd	2п2 м или пм	4n
22n	[2, n]⁺	D_п	n2	2n
* нн	[n]	C_NV	нм	2n
п *	[п⁺,2]	C_нэ	н / м или 2п	2n
п ×	[2⁺, 2н⁺]	S_2n	2п или же п	2n
nn	[n]⁺	C_п	п	п
Особые случаи
*222	[2,2]	D_2ч	2 / ммм или 22m2	8
2*2	[2⁺,4]	D_2d	222 м или 2м	8
222	[2,2]⁺	D₂	22	4
*22	[2]	C_2v	2м	4
2*	[2⁺,2]	C_2ч	2 / м или 22	4
2×	[2⁺,4⁺]	S₄	22 или же 2	4
22	[2]⁺	C₂	2	2
*22	[1,2]	D_{1 час}= C_2v	1 / ммм или 21m2	4
2*	[2⁺,2]	D_1д= C_2ч	212 м или 1м	4
22	[1,2]⁺	D₁= C₂	12	2
*1	[ ]	C_1v= C_s	1 мес.	2
1*	[2,1⁺]	C_{1 час}= C_s	1 / м или 21	2
1×	[2⁺,2⁺]	S₂= C_я	21 или же 1	2
1	[ ]⁺	C₁	1	1

Евклидова плоскость

Фриз-группы

Фриз-группы
IUC	Кокс	Schön^* Struct.	Диаграмма^§ Орбифолд	Примеры и Конвей прозвище^[2]	Описание
p1	[∞]⁺	C_∞ Z_∞	∞∞	F F F F F F F F прыгать	(T) Только переводы: Эта группа генерируется отдельно путем сдвига на наименьшее расстояние, на которое шаблон является периодическим.
p11g	[∞⁺,2⁺]	S_∞ Z_∞	∞×	Γ L Γ L Γ L Γ L шаг	(TG) Размышления и переводы: Эта группа создается по отдельности в результате отражения скольжения, а переводы получают путем объединения двух отражений скольжения.
p1m1	[∞]	C_∞v Dih_∞	*∞∞	Λ Λ Λ Λ Λ Λ Λ Λ сбоку	(TV) Вертикальные линии отражения и переводы: Группа такая же, как нетривиальная группа в одномерном случае; он создается перемещением и отражением по вертикальной оси.
p2	[∞,2]⁺	D_∞ Dih_∞	22∞	S S S S S S S S прядильный хмель	(TR) Перевод и поворот на 180 °: Группа создается за счет перевода и поворота на 180 °.
p2mg	[∞,2⁺]	D_∞d Dih_∞	2*∞	V Λ V Λ V Λ V Λ вращающийся бочонок	(TRVG) Вертикальные отражающие линии, скользящие отражения, переводы и поворот на 180 °: Переводы здесь возникают из-за скользящих отражений, поэтому эта группа создается скользящим отражением и либо вращением, либо вертикальным отражением.
p11m	[∞⁺,2]	C_∞h Z_∞× Ди₁	∞*	Б Б Б Б Б Б Б Б Прыгать	(THG) Переводы, Горизонтальные отражения, Скользящие отражения: Эта группа создается перемещением и отражением по горизонтальной оси. Скользящее отражение здесь возникает как композиция переноса и горизонтального отражения.
p2мм	[∞,2]	D_∞h Dih_∞× Ди₁	*22∞	В Ч Ч Ч Ч В Ч Ч вращающийся прыжок	(TRHVG) Горизонтальные и вертикальные линии отражения, переводы и поворот на 180 °: Для этой группы требуются три генератора, одна из которых состоит из трансляции, отражения по горизонтальной оси и отражения по вертикальной оси.

^*Обозначения точечной группы Шенфлиса расширены здесь как бесконечные случаи эквивалентных диэдральных точечных симметрий

^§На схеме показан один фундаментальная область желтым, с линиями отражения синим, скользящими линиями отражения пунктирным зеленым, нормали сдвига красным, а точки двойного вращения в виде маленьких зеленых квадратов.

Группы обоев

Фундаментальные области евклидовых рефлексивных групп
(* 442), п4м	(4 * 2), p4g

(* 333), п3м	(632), стр. 6

17 группы обоев^[3]
Орбифолд Подпись	Coxeter	Германн Mauguin	Speiser Ниггли	Поля Guggenhein	Фейес Тот Кэдвелл
*632	[6,3]	p6m	C^(Я)_6v	D₆	W¹₆
632	[6,3]⁺	p6	C^(Я)₆	C₆	W₆
*442	[4,4]	p4m	C^(Я)₄	D^*₄	W¹₄
4*2	[4⁺,4]	p4g	C^II_4в	D^о₄	W²₄
442	[4,4]⁺	p4	C^(Я)₄	C₄	W₄
*333	[3^[3]]	p3m1	C^II_3в	D^*₃	W¹₃
3*3	[3⁺,6]	p31m	C^я_3в	D^о₃	W²₃
333	[3^[3]]⁺	p3	C^я₃	C₃	W₃
*2222	[∞,2,∞]	пмм	C^я_2v	D₂кккк	W²₂
2*22	[∞,2⁺,∞]	см	C^IV_2v	D₂кгкг	W¹₂
22*	[(∞,2)⁺,∞]	pmg	C^III_2v	D₂ккгг	W³₂
22×	[∞⁺,2⁺,∞⁺]	pgg	C^II_2v	D₂gggg	W⁴₂
2222	[∞,2,∞]⁺	p2	C^(Я)₂	C₂	W₂
**	[∞⁺,2,∞]	вечера	C^я_s	D₁кк	W²₁
*×	[∞⁺,2⁺,∞]	см	C^III_s	D₁кг	W¹₁
××	[∞⁺,(2,∞)⁺]	pg	C^II₂	D₁gg	W³₁
о	[∞⁺,2,∞⁺]	p1	C^(Я)₁	C₁	W₁

Гиперболическая плоскость

Модель диска Пуанкаре фундаментальной области треугольники
Пример прямоугольных треугольников (* 2pq)
*237	*238	*239	*23∞
*245	*246	*247	*248	*∞42
*255	*256	*257	*266	*2∞∞
Пример общих треугольников (* pqr)
*334	*335	*336	*337	*33∞
*344	*366	*3∞∞	*6³	*∞³
Пример высших многоугольников (* pqrs ...)
*2223	*(23)²	*(24)²	*3⁴	*4⁴
*2⁵	*2⁶	*2⁷	*2⁸
*222∞	*(2∞)²	*∞⁴	*2^∞	*∞^∞

Первые несколько гиперболических групп, упорядоченных по их эйлеровой характеристике:

Группы гиперболической симметрии^[4]
-1 / χ	Орбифолды	Coxeter
84	*237	[7,3]
48	*238	[8,3]
42	237	[7,3]⁺
40	*245	[5,4]
36 - 26.4	239, 2 3 10	[9,3], [10,3]
26.4	*2 3 11	[11,3]
24	2 3 12, 246, 334, 34, 238	[12,3], [6,4], [(4,3,3)], [3⁺,8], [8,3]⁺
22.3 - 21	2 3 13, 2 3 14	[13,3], [14,3]
20	2 3 15, 255, 5*2, 245	[15,3], [5,5], [5⁺,4], [5,4]⁺
19.2	*2 3 16	[16,3]
18+2/3	*247	[7,4]
18	*2 3 18, 239	[18,3], [9,3]⁺
17.5 - 16.2	2 3 19, 2 3 20, 2 3 21, 2 3 22, *2 3 23	[19,3], [20,3], [20,3], [21,3], [22,3], [23,3]
16	2 3 24, 248	[24,3], [8,4]
15	2 3 30, 256, 335, 35, 2 3 10	[30,3], [6,5], [(5,3,3)], [3⁺,10], [10,3]⁺
14+2/5 - 13+1/3	2 3 36 ... 2 3 70, 249, 2 4 10	[36,3] ... [60,3], [9,4], [10,4]
13+1/5	*2 3 66, 2 3 11	[66,3], [11,3]⁺
12+8/11	2 3 105, 257	[105,3], [7,5]
12+4/7	2 3 132, 2 4 11 ...	[132,3], [11,4], ...
12	23∞, 2 4 12, 266, 62, 336, 36, 344, 43, 2223, 223, 2 3 12, 246, 334	[∞,3] [12,4], [6,6], [6⁺,4], [(6,3,3)], [3⁺,12], [(4,4,3)], [4⁺,6], [∞,3,∞], [12,3]⁺, [6,4]⁺ [(4,3,3)]⁺
...

Смотрите также

Мутации орбифолдов
Обозначение фибрифолда - расширение орбифолдной записи для 3d космические группы

внешняя ссылка

Полевой справочник по орбифолдам (Заметки из класса по «Геометрия и воображение» в Миннеаполисе, с Джоном Конвеем, Питером Дойлом, Джейн Гилман и Биллом Терстоном, 17–28 июня 1991 г. См. также PDF, 2006 г. )
2DTiler Программа для визуализации двумерных мозаик плоскости и редактирования их групп симметрии в орбифолдной нотации

[1] Симметрии вещей, Приложение A, страница 416

[2] Фризные Узоры Математик Джон Конвей придумал имена, относящиеся к шагам для каждой из групп фризов.

[3] Симметрии вещей, Приложение A, страница 416

[4] Симметрии вещей, Глава 18, Подробнее о гиперболических группах, Перечисление гиперболических групп, стр. 239

[1]

[2]

[3]

[4]