Дигедрон - Dihedron
| Набор обычных п-гональные диэдры | |
|---|---|
 Пример шестиугольного диэдра на сфере | |
| Тип | Правильный многогранник или же сферическая черепица |
| Лица | 2 п-угольники |
| Края | п |
| Вершины | п |
| Конфигурация вершины | п.п |
| Символ Wythoff | 2 | п 2 |
| Символ Шлефли | {п,2} |
| Диаграмма Кокстера | |
| Группа симметрии | Dпчас, [2,п], (*22п), порядок 4п |
| Группа вращения | Dп, [2,п]+, (22п), порядок 2п |
| Двойной многогранник | п-гональный осоэдр |
А диэдр это тип многогранник, состоящий из двух полигональных граней с одним и тем же набором ребер. В трехмерном Евклидово пространство, это выродиться если его грани плоские, а в трехмерном сферическое пространство, диэдр с плоскими гранями можно рассматривать как линзу, примером которой является фундаментальная область пространство объектива L (п,q).[1] Дигедры также называли бигедра,[2] плоские многогранники,[3] или же дважды покрытые полигоны.[3]
А правильный диэдр это диэдр, образованный двумя правильные многоугольники это может быть описано Символ Шлефли {п,2}.[4] Как сферический многогранник, каждый многоугольник такого двугранника заполняет полушарие, с регулярным п-гон на большой круг экватор между ними.
В двойной из п-гональный диэдр - это п-гональный осоэдр, куда п Digon грани имеют две общие вершины.
Как многогранник
А диэдр можно считать вырожденным призма состоящий из двух (плоских) п-сторонний полигоны соединены «спина к спине», так что полученный объект не имеет глубины. Многоугольники должны быть конгруэнтными, но склеенными таким образом, чтобы один был зеркальным отражением другого.
Дигедра может возникать из Теорема единственности Александрова, который характеризует расстояния на поверхности любого выпуклого многогранника как локально евклидовы, за исключением конечного числа точек с положительным угловой дефект в сумме 4π. Эта характеризация верна также для расстояний на поверхности диэдра, поэтому утверждение теоремы Александрова требует, чтобы диэдры считались выпуклыми многогранниками.[5]
Как мозаика на сфере
Как сферическая черепица, а диэдр может существовать как невырожденная форма, с двумя п-сторонние грани, покрывающие сферу, каждая грань полушарие, а вершины вокруг большой круг. (Это обычный если вершины расположены на одинаковом расстоянии.)
Правильный многогранник {2,2} самодвойственен и одновременно является осоэдр и диэдр.
| Изображение |  | 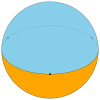 |  |  | 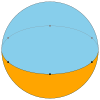 |
| Schläfli | {2,2} | {3,2} | {4,2} | {5,2} | {6,2}... |
|---|---|---|---|---|---|
| Coxeter | |||||
| Лица | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} |
| Края и вершины | 2 | 3 | 4 | 5 | 6 |
Апейрогональный диэдр
В пределе диэдр становится апейрогональный диэдр как 2-мерная тесселяция:
Дитопы
Обычный дитоп является п-мерный аналог диэдра с символом Шлефли {п,...q,р, 2}. Имеет два грани, {п,...q,р}, которые разделяют все гребни, {п,...q} вместе.[6]
Смотрите также
Рекомендации
- ^ Гаусманн, Эвелиза; Роланд Лехук; Жан-Пьер Люмине; Жан-Филипп Узан; Джеффри Уикс (2001). «Топологическое линзирование в сферических пространствах». Классическая и квантовая гравитация. 18 (23): 5155–5186. arXiv:gr-qc / 0106033. Bibcode:2001CQGra..18.5155G. Дои:10.1088/0264-9381/18/23/311. S2CID 34259877.
- ^ Кантор, С. (2003), «Об объеме неограниченных многогранников в гиперболическом пространстве» (PDF), Beiträge zur Algebra und Geometrie, 44 (1): 145–154, МИСТЕР 1990989.
- ^ а б О'Рурк, Джозеф (2010), Пара плоских застежек-молний для Платоновых тел, arXiv:1010.2450, Bibcode:2010arXiv1010.2450O
- ^ Кокстер, Х. С. М. (Январь 1973 г.), Правильные многогранники (3-е изд.), Dover Publications Inc., стр.12, ISBN 0-486-61480-8
- ^ О'Рурк, Джозеф (2010), О плоских многогранниках, вытекающих из теоремы Александрова, arXiv:1007.2016, Bibcode:2010arXiv1007.2016O
- ^ Макмаллен, Питер; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Издательство Кембриджского университета, п.158, ISBN 0-521-81496-0

