Эйлерова характеристика - Euler characteristic - Wikipedia

В математика, а точнее в алгебраическая топология и многогранная комбинаторика, то Эйлерова характеристика (или же Число Эйлера, или же Характеристика Эйлера – Пуанкаре) это топологический инвариант, число, которое описывает топологическое пространство форма или структура, независимо от того, как он изогнут. Обычно его обозначают как ${ displaystyle chi}$ (Греческая строчная буква чи ).

Первоначально эйлерова характеристика была определена для многогранники и использовались для доказательства различных теорем о них, включая классификацию Платоновы тела. Это было сказано для Платоновых тел в 1537 г. в неопубликованной рукописи Франческо Мауролико.^[1] Леонард Эйлер, для которых это понятие названо, ввел его для выпуклых многогранников в более общем смысле, но не смог строго доказать, что оно является инвариантом. В современной математике характеристика Эйлера возникает из гомология и, более абстрактно, гомологическая алгебра.

Многогранники

В Эйлерова характеристика ${ displaystyle chi}$ был классически определен для поверхностей многогранников по формуле

{ displaystyle chi = V-E + F}

куда V, E, и F соответственно числа вершины (углы), края и лица в данном многограннике. Любой выпуклый многогранник поверхность имеет эйлерову характеристику

{ displaystyle V-E + F = 2.}

Это уравнение, сформулированное Леонард Эйлер в 1758 г.,^[2] известен как Формула многогранника Эйлера.^[3] Это соответствует эйлеровой характеристике сфера (т. е. χ = 2) и применяется идентично к сферические многогранники. Ниже приводится иллюстрация формулы на некоторых многогранниках.

Имя	Вершины V	Края E	Лица F	Эйлерова характеристика: V − E + F
Тетраэдр	4	6	4	2
Шестигранник или же куб	8	12	6	2
Октаэдр	6	12	8	2
Додекаэдр	20	30	12	2
Икосаэдр	12	30	20	2

Поверхности невыпуклых многогранников могут иметь различные эйлеровы характеристики:

Имя	Вершины V	Края E	Лица F	Эйлерова характеристика: V − E + F
Тетрагемигексаэдр	6	12	7	1
Октагемиоктаэдр	12	24	12	0
Кубогемиоктаэдр	12	24	10	−2
Малый звездчатый додекаэдр	12	30	12	−6
Большой звездчатый додекаэдр	20	30	12	2

Для правильных многогранников Артур Кэли получил модифицированную форму формулы Эйлера, используя плотность D, вершина фигуры плотность d_v, и плотность лица ${ displaystyle d_ {f}}$ :

{ displaystyle d_ {v} V-E + d_ {f} F = 2D.}

Этот вариант верен как для выпуклых многогранников (где все плотности равны 1), так и для невыпуклых многогранников. Многогранники Кеплера-Пуансо.

Проективные многогранники все имеют эйлерову характеристику 1, как и реальная проективная плоскость, а поверхности тороидальные многогранники все имеют эйлерову характеристику 0, как и тор.

Плоские графики

Эйлерову характеристику можно определить для связных плоские графики тем же ${ Displaystyle V-E + F}$ формула как для многогранных поверхностей, где F - количество граней в графе, включая внешнюю грань.

Эйлерова характеристика любого плоского связного графа G равна 2. Это легко доказать индукцией по количеству граней, определяемых G, начиная с дерева в качестве базового случая. Для деревьев, ${ Displaystyle E = V-1}$ и ${ Displaystyle F = 1}$ . Если G имеет C компонент (несвязные графы), то же рассуждение индукцией по F показывает, что ${ Displaystyle V-E + F-C = 1}$ . Одна из немногих работ Коши по теории графов также доказывает этот результат.

Через стереографическая проекция плоскость отображается в двумерную сферу, так что связный граф отображается в многоугольное разложение сферы, имеющей эйлерову характеристику 2. Эта точка зрения подразумевается в приведенном ниже доказательстве Коши формулы Эйлера.

Доказательство формулы Эйлера

Первые шаги доказательства в случае куба

Есть много доказательств формулы Эйлера. Один был предоставлен Коши в 1811 г. следующим образом. Это применимо к любому выпуклому многограннику и, в более общем смысле, к любому многограннику, граница которого топологически эквивалентна сфере, а грани топологически эквивалентны кругам.

Удалите одну грань многогранной поверхности. Оттягивая края отсутствующей грани друг от друга, деформируйте все остальное в плоский граф точек и кривых таким образом, чтобы периметр отсутствующей грани располагался снаружи, окружая полученный граф, как показано на рисунке. первый из трех графиков для частного случая куба. (Предположение, что полиэдральная поверхность гомеоморфна сфере вначале, делает это возможным.) После этой деформации правильные грани обычно перестают быть правильными. Количество вершин и ребер осталось прежним, но количество граней уменьшилось на 1. Таким образом, доказательство формулы Эйлера для многогранника сводится к доказательству V − E + F = 1 для этого деформированного плоского объекта.

Если есть грань с более чем тремя сторонами, нарисуйте диагональ, то есть кривую через грань, соединяющую две вершины, которые еще не соединены. Это добавляет одно ребро и одну грань и не меняет количество вершин, поэтому не меняет количество V − E + F. (Здесь необходимо предположение, что все грани являются дисками, чтобы показать через Теорема Жордана что эта операция увеличивает количество граней на единицу.) Продолжайте добавлять ребра таким образом, пока все грани не станут треугольными.

Примените несколько раз любое из следующих двух преобразований, сохраняя инвариант, что внешняя граница всегда простой цикл:

Удалите треугольник, у которого только одно ребро примыкает к внешней стороне, как показано на втором графике. Это уменьшает количество ребер и граней на одну каждую и не меняет количество вершин, поэтому V − E + F.
Удалите треугольник с двумя ребрами, общими для внешней части сети, как показано на третьем графике. При каждом удалении треугольника удаляется вершина, два ребра и одна грань, поэтому сохраняется V − E + F.

Эти преобразования в конечном итоге сводят плоский граф к одному треугольнику. (Без инварианта простого цикла удаление треугольника могло бы разъединить оставшиеся треугольники, сделав недействительным остальную часть аргумента. Правильный порядок удаления - это элементарный пример артобстрел.)

В этот момент одинокий треугольник имеет V = 3, E = 3 и F = 1, так что V − E + F = 1. Поскольку на каждом из двух шагов преобразования эта величина сохраняется, мы показали V − E + F = 1 для деформированного плоского объекта, что демонстрирует V − E + F = 2 для многогранника. Это доказывает теорему.

Дополнительные доказательства см. Двадцать доказательств формулы Эйлера к Дэвид Эппштейн.^[4] Множественные доказательства, включая их недостатки и ограничения, используются в качестве примеров в Доказательства и опровержения к Имре Лакатош.^[5]

Топологическое определение

Обсуждаемые выше многогранные поверхности, говоря современным языком, являются двумерными конечными CW-комплексы. (Когда используются только треугольные грани, они являются двумерными конечными симплициальные комплексы.) В общем случае для любого конечного CW-комплекса Эйлерова характеристика можно определить как знакопеременную сумму

{ displaystyle chi = k_ {0} -k_ {1} + k_ {2} -k_ {3} + cdots,}

куда k_п обозначает количество ячеек размерности п в комплексе.

Аналогично для симплициального комплекса Эйлерова характеристика равняется переменной сумме

{ displaystyle chi = k_ {0} -k_ {1} + k_ {2} -k_ {3} + cdots,}

куда k_п обозначает количество п-комплексы в комплексе.

В более общем плане, для любого топологическое пространство, мы можем определить пth Бетти число б_п как классифицировать из п-й особые гомологии группа. В Эйлерова характеристика можно тогда определить как переменную сумму

{ displaystyle chi = b_ {0} -b_ {1} + b_ {2} -b_ {3} + cdots.}

Эта величина хорошо определена, если все числа Бетти конечны и если они равны нулю за пределами определенного индекса.п₀. Для симплициальных комплексов это не то же определение, что и в предыдущем абзаце, но вычисление гомологии показывает, что два определения дадут одинаковое значение для ${ displaystyle chi}$ .

Характеристики

Эйлерова характеристика хорошо ведет себя по отношению ко многим основным операциям в топологических пространствах следующим образом.

Гомотопическая инвариантность

Гомологии - это топологический инвариант, более того, гомотопический инвариант: Два топологических пространства, которые гомотопический эквивалент имеют изоморфный группы гомологий. Отсюда следует, что эйлерова характеристика также является гомотопическим инвариантом.

Например, любой стягиваемый пространство (то есть, одна гомотопия, эквивалентная точке) имеет тривиальные гомологии, что означает, что 0-е число Бетти равно 1, а остальные 0. Следовательно, его эйлерова характеристика равна 1. Этот случай включает Евклидово пространство ${ Displaystyle mathbb {R} ^ {п}}$ любого измерения, а также единичный твердый шар в любом евклидовом пространстве - одномерный интервал, двумерный диск, трехмерный шар и т. д.

Другой пример: любой выпуклый многогранник гомеоморфен трехмерному мяч, поэтому его поверхность гомеоморфна (следовательно, гомотопически эквивалентна) двумерному сфера, который имеет эйлерову характеристику 2. Это объясняет, почему выпуклые многогранники имеют эйлерову характеристику 2.

Принцип включения-исключения

Если M и N - любые два топологических пространства, то эйлерова характеристика их несвязный союз является суммой их эйлеровых характеристик, поскольку гомологии аддитивны при несвязном объединении:

{ Displaystyle чи (М sqcup N) = чи (М) + чи (N).}

В более общем смысле, если M и N подпространства большего пространства Икс, то их объединение и пересечение тоже. В некоторых случаях характеристика Эйлера подчиняется версии принцип включения-исключения:

{ Displaystyle чи (M чашка N) = чи (M) + чи (N) - чи (M cap N).}

Это верно в следующих случаях:

если M и N являются эксцизная пара. В частности, если интерьеры из M и N внутри союза все еще покрывают союз.^[6]
если Икс это локально компактное пространство, и один использует характеристики Эйлера с компактный поддерживает, никаких предположений о M или же N необходимы.
если Икс это стратифицированное пространство все страты которых четномерны, принцип включения-исключения выполняется, если M и N союзы слоев. Это особенно важно, если M и N являются подмногообразиями сложный алгебраическое многообразие.^[7]

В целом принцип включения – исключения неверен. А контрпример дается взятием Икс быть реальная линия, M а подмножество состоящий из одной точки и N то дополнять из M.

Связанная сумма

Для двух связных замкнутых n-многообразий ${ displaystyle M, N}$ можно получить новое связное многообразие ${ displaystyle M #N}$ через связанная сумма Эйлерова характеристика связана формулой ^[8]

{ Displaystyle чи (M #N) = чи (M) + чи (N) - чи (S ^ {n}).}

Свойство продукта

Кроме того, эйлерова характеристика любого пространство продукта M × N является

{ Displaystyle чи (М раз N) = чи (М) CDOT чи (N).}

Эти свойства сложения и умножения также используются мощность из наборы. Таким образом, эйлерову характеристику можно рассматривать как обобщение мощности; видеть [1].

Покрытие пространств

Аналогично для k-стелен покрывающее пространство ${ displaystyle { tilde {M}} to M,}$ надо

{ Displaystyle чи ({ тильда {M}}) = к cdot чи (M).}

В более общем плане для разветвленное перекрытие, эйлерова характеристика покрытия может быть вычислена из вышеизложенного с поправочным коэффициентом для точек разветвления, который дает Формула Римана – Гурвица.

Свойство фибрации

Свойство product имеет гораздо более общее значение для расслоения с определенными условиями.

Если ${ displaystyle p двоеточие E to B}$ расслоение с волокном F, с основанием B соединенный путём, а расслоение ориентируемо над полем K, то эйлерова характеристика с коэффициентами в поле K удовлетворяет свойству продукта:^[9]

{ Displaystyle чи (Е) = чи (F) cdot чи (B).}

Это включает в себя пространства продуктов и покрывающие пространства как частные случаи, и это может быть доказано Спектральная последовательность Серра о гомологиях расслоения.

Для пучков волокон это также можно понять с точки зрения карта переноса ${ Displaystyle тау двоеточие H _ {*} (B) to H _ {*} (E)}$ - обратите внимание, что это подъем и идет «не в ту сторону» - чья композиция с картой проекции ${ displaystyle p _ {*} двоеточие H _ {*} (E) to H _ {*} (B)}$ это умножение на Класс Эйлера волокна:^[10]

{ Displaystyle п _ {*} circ tau = chi (F) cdot 1.}

Примеры

Поверхности

Эйлерову характеристику можно легко вычислить для общих поверхностей, найдя полигонизацию поверхности (то есть описание как CW-комплекс ) и используя приведенные выше определения.

Имя	Изображение	Эйлерова характеристика
Интервал		1
Круг		0
Диск		1
Сфера		2
Тор (Произведение двух кругов)		0
Двойной тор		−2
Тройной тор		−4
Реальная проективная плоскость		1
Лента Мебиуса		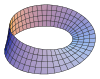0
Бутылка Клейна		0
Две сферы (не связаны) (Непересекающееся объединение двух сфер)		2 + 2 = 4
Три сферы (не связаны) (Непересекающееся объединение трех сфер)		2 + 2 + 2 = 6

Футбольный мяч

Обычно строят футбольные мячи сшиванием пятиугольных и шестиугольных частей, по три части, встречающиеся в каждой вершине (см., например, Adidas Telstar ). Если п пятиугольники и ЧАС используются шестиугольники, то есть F = п + ЧАС лица V = (5 п + 6 ЧАС) / 3 вершины и E = (5 п + 6 ЧАС) / 2 ребра. Таким образом, эйлерова характеристика

{ displaystyle V-E + F = { frac {5P + 6H} {3}} - { frac {5P + 6H} {2}} + P + H = { frac {P} {6}}. }

Поскольку сфера имеет эйлерову характеристику 2, отсюда следует, что п = 12. То есть футбольный мяч, построенный таким образом, всегда имеет 12 пятиугольников. В принципе, количество шестиугольников неограниченно. Этот результат применим к фуллерены и Многогранники Гольдберга.

Произвольные размеры

В п-мерная сфера имеет особые группы гомологий, равные

{ displaystyle H_ {k} (S ^ {n}) = { begin {cases} mathbb {Z} & k = 0, n {0 } & { text {в противном случае}} end { случаи}}}

следовательно, имеет число Бетти 1 в измерениях 0 и п, а все остальные числа Бетти равны 0. Тогда его эйлерова характеристика равна 1 + (−1)^п - то есть либо 0, либо 2.

В п-размерный реальный проективное пространство является частным от п-сфера антиподальная карта. Отсюда следует, что его эйлерова характеристика ровно вдвое меньше, чем у соответствующей сферы - либо 0, либо 1.

В п-мерный тор - это произведение пространств п круги. Его эйлерова характеристика равна 0 по свойству произведения. В общем, любой компакт параллелизируемое многообразие, включая любые компактные Группа Ли, имеет эйлерову характеристику 0.^[11]

Эйлерова характеристика любого закрыто нечетномерное многообразие также равно 0.^[12] Случай ориентируемых примеров является следствием Двойственность Пуанкаре. Это свойство применяется в целом к любому компактный стратифицированное пространство все слои которых имеют нечетное измерение. Это также применимо к замкнутым нечетномерным неориентируемым многообразиям через соотношение два к одному. ориентируемая двойная крышка.

Связь с другими инвариантами

Эйлерова характеристика замкнутого ориентируемый поверхность можно рассчитать из род грамм (количество тори в связанная сумма разложение поверхности; интуитивно количество «ручек») как

{ displaystyle chi = 2-2g.}

Эйлерова характеристика замкнутой неориентируемой поверхности может быть вычислена по ее неориентируемому роду k (количество реальные проективные плоскости в связной сумме разложения поверхности) как

{ Displaystyle чи = 2-к.}

Для замкнутых гладких многообразий эйлерова характеристика совпадает с Число Эйлера, т.е. Класс Эйлера своего касательный пучок оценивается на фундаментальный класс многообразия. Класс Эйлера, в свою очередь, относится ко всем остальным характеристические классы из векторные пакеты.

Для закрытых Римановы многообразия, эйлерова характеристика также может быть найдена интегрированием кривизны; увидеть Теорема Гаусса – Бонне для двумерного случая и обобщенная теорема Гаусса – Бонне для общего случая.

Дискретным аналогом теоремы Гаусса – Бонне является Декарта теорема о том, что «полный дефект» многогранник, измеренная полными кружками, - эйлерова характеристика многогранника; видеть дефект (геометрия).

Теорема Хадвигера характеризует эйлерову характеристику как уникальный (вплоть до скалярное умножение ) трансляционно-инвариантная, конечно аддитивная, необязательно неотрицательная функция множества, определенная на конечные союзы из компактный выпуклый устанавливается в р^п то есть «однородной степени 0».

Обобщения

Для каждого комбинаторного клеточный комплекс, характеристика Эйлера определяется как количество 0-ячеек минус количество 1-ячеек, плюс количество 2-ячеек и т. д., если эта чередующаяся сумма конечна. В частности, эйлерова характеристика конечного множества - это просто его мощность, а эйлерова характеристика конечного множества. график это количество вершин минус количество ребер.^[13]

В более общем плане можно определить эйлерову характеристику любого цепной комплекс быть переменной суммой разряды групп гомологий цепного комплекса, предполагая, что все эти ранги конечны.^[14]

Версия характеристики Эйлера, используемая в алгебраическая геометрия как следует. Для любого связный пучок ${ displaystyle { mathcal {F}}}$ на собственном схема Икс, его эйлерова характеристика определяется как

{ displaystyle chi ({ mathcal {F}}) = sum _ {i} (- 1) ^ {i} h ^ {i} (X, { mathcal {F}}),}

куда ${ Displaystyle ч ^ {я} (Х, { mathcal {F}})}$ это размер я-го когомологии пучков группа ${ displaystyle { mathcal {F}}}$ . В этом случае все размеры конечны на Теорема Гротендика о конечности. Это пример эйлеровой характеристики цепного комплекса, где цепной комплекс является конечным разрешением ${ displaystyle { mathcal {F}}}$ ациклическими связками.

Другое обобщение понятия эйлеровой характеристики на многообразиях происходит из орбифолды (видеть Эйлерова характеристика орбифолда ). Хотя каждое многообразие имеет целочисленную эйлерову характеристику, орбифолд может иметь дробную эйлерову характеристику. Например, орбифолд-капля имеет эйлерову характеристику 1 + 1 /п, куда п - простое число, соответствующее углу конуса 2 $π$ / п.

Понятие эйлеровой характеристики ограниченного конечного посеть еще одно обобщение, важное в комбинаторика. Посет считается «ограниченным», если он имеет наименьшие и наибольшие элементы; назовем их 0 и 1. Эйлерова характеристика такого ч.у. определяется как целое число μ(0,1), где μ это Функция Мёбиуса в этом позе алгебра инцидентности.

В дальнейшем это можно обобщить, определив Q-значная эйлерова характеристика для некоторых конечных категории, понятие, совместимое с эйлеровыми характеристиками графов, орбифолдов и множеств, упомянутых выше. В этом случае эйлерова характеристика конечного группа или же моноид грамм равно 1 / |грамм| и эйлерова характеристика конечного группоид является суммой 1 / |грамм_я|, где мы выбрали одну репрезентативную группу грамм_я для каждой компоненты связности группоида.^[15]

Смотрите также

дальнейшее чтение

Флегг, Х. Грэм; От геометрии к топологии, Довер 2001, стр. 40.

внешняя ссылка

[1] Фридман, Майкл (2018). История фолдинга в математике: математизация полей. Birkhäuser. п. 71. Дои:10.1007/978-3-319-72487-4. ISBN 978-3-319-72486-7.

[2] Эйлер, Леонард (1758-01-01). "Elementa doctrinae solidorum". Новые комментарии academiae scientiarum Petropolitanae: 109–140.

[3] Ричсон 2008

[Eppstein2013-4] Эппштейн, Дэвид. «Двадцать доказательств формулы Эйлера: V-E + F = 2». Получено 3 июн 2013.

[5] Имре Лакатош: Доказательства и опровержения, Cambridge Technology Press, 1976 г.

[6] Эдвин Спаниер: Алгебраическая топология, Springer 1966, стр. 205.

[7] Уильям Фултон: Введение в торические многообразия, 1993, Princeton University Press, стр. 141.

[8] «Гомологии связной суммы». Получено 2016-07-13.

[9] Спаниер, Эдвин Генри (1982), Алгебраическая топология, Спрингер, ISBN 978-0-387-94426-5, Приложения спектральной последовательности гомологий, стр. 481

[10] Готтлиб, Дэниел Генри (1975), «Пучки волокон и эйлерова характеристика» (PDF), Журнал дифференциальной геометрии, 10 (1): 39–48

[11] Милнор, Джон В. и Сташефф, Джеймс Д.: Характерные классы, Princeton University Press, 1974

[12] Richeson 2008, стр. 261

[13] Олаф Пост называет это «известной формулой»: Пост, Олаф (2009), «Спектральный анализ метрических графов и связанных пространств», Пределы графов в теории групп и информатике, Лозанна, Швейцария: EPFL Press, стр. 109–140, arXiv:0712.1507, Bibcode:2007arXiv0712.1507P.

[14] Lab, "Эйлерова характеристика "

[15] Том Ленстер "Эйлерова характеристика категории ", Documenta Mathematica, 13 (2008), стр. 21–49.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]