Архимедово твердое тело - Archimedean solid

Усеченный тетраэдр, кубооктаэдр и усеченный икосододекаэдр. Первое и последнее можно описать как наименьшее и наибольшее архимедово твердое тело соответственно.

Ромбокубооктаэдр и псевдоромбокубооктаэдр

В геометрия, Архимедово твердое тело является одним из 13 твердых тел, впервые перечисленных Архимед. Они выпуклый равномерные многогранники состоит из правильные многоугольники встреча в идентичных вершины, за исключением пяти Платоновы тела (которые состоят только из одного типа многоугольника) и исключая призмы и антипризмы. Они отличаются от Твердые тела Джонсона, правильные многоугольные грани которого не пересекаются в одинаковых вершинах.

«Идентичные вершины» означает, что каждые две вершины симметричны друг другу: глобальная изометрия всего твердого тела переводит одну вершину в другую, при этом твердое тело укладывается непосредственно в исходное положение. Бранко Грюнбаум  (2009 ) заметил, что 14-й многогранник удлиненная квадратная гиробикупола (или псевдоромбокубооктаэдр), соответствует более слабому определению архимедова твердого тела, в котором «идентичные вершины» просто означают, что грани, окружающие каждую вершину, имеют одинаковые типы (т.е. каждая вершина выглядит одинаково с близкого расстояния), поэтому только требуется локальная изометрия. Грюнбаум указал на частую ошибку, когда авторы определяют архимедовы тела, используя это локальное определение, но опускают 14-й многогранник. Если нужно перечислить только 13 многогранников, определение должно использовать глобальные симметрии многогранника, а не локальные окрестности.

Призмы и антипризмы, чей группы симметрии являются диэдральные группы, обычно не считаются архимедовыми телами, даже если их грани являются правильными многоугольниками, а их группы симметрии действуют транзитивно на их вершинах. Не считая этих двух бесконечных семейств, существует 13 архимедовых тел. Все твердые тела Архимеда (но не вытянутую квадратную гиробикуполу) можно получить с помощью Конструкции Wythoff из Платоновых тел с четырехгранный, восьмигранный и икосаэдрическая симметрия.

Происхождение имени

Архимедовы тела получили свое название от Архимед, который обсуждал их в уже потерянной работе. Паппус ссылается на него, утверждая, что Архимед перечислил 13 многогранников.^[1] Вовремя эпоха Возрождения, художники и математики ценится чистые формы с высокой симметрией, и примерно к 1620 году Иоганн Кеплер завершил повторное открытие 13 многогранников,^[2] а также определение призмы, антипризмы, и невыпуклые тела, известные как Многогранники Кеплера-Пуансо. (Видеть Шрайбер, Фишер и Стернат, 2008 г. для получения дополнительной информации о повторном открытии архимедовых тел в эпоху Возрождения.)

Кеплер, возможно, также нашел удлиненная квадратная гиробикупола (псевдоромбокубооктаэдр): по крайней мере, он однажды заявил, что существует 14 архимедовых тел. Однако его опубликованное перечисление включает только 13 однородных многогранников, и первое четкое заявление о существовании псевдоромбокубооктаэдра было сделано в 1905 г. Дункан Соммервилл.^[1]

Классификация

Всего существует 13 архимедовых тел (не считая удлиненная квадратная гиробикупола; 15, если зеркальные изображения из двух энантиоморфы, курносый куб и курносый додекаэдр, считаются отдельно).

Здесь конфигурация вершины относится к типу правильных многоугольников, которые встречаются в любой данной вершине. Например, конфигурация вершины из (4,6,8) означает, что a квадрат, шестиугольник, и восьмиугольник встречаются в вершине (с порядком обхода вершины по часовой стрелке).

Имя/ (альтернативное имя)	Schläfli Coxeter	Прозрачный	Твердый	Сеть	Вершина конф. /инжир.	Лица		Края	Vert.	Объем (края блока)	Точка группа	Сферичность
усеченный тетраэдр	т {3,3}				3.6.6	8	4 треугольника 4 шестиугольники	18	12	2.710576	Тd	0.7754132
кубооктаэдр (ромбитетраэтраэдр)	r {4,3} или rr {3,3} или же				3.4.3.4	14	8 треугольники 6 квадраты	24	12	2.357023	Очас	0.9049973
усеченный куб	т {4,3}				3.8.8	14	8 треугольников 6 восьмиугольники	36	24	13.599663	Очас	0.8494937
усеченный октаэдр (усеченный тетратетраэдр)	t {3,4} или tr {3,3} 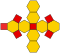или же				4.6.6	14	6 квадратов 8 шестиугольников	36	24	11.313709	Очас	0.9099178
ромбокубооктаэдр (малый ромбокубооктаэдр)	рр {4,3}				3.4.4.4	26	8 треугольников 18 квадратов	48	24	8.714045	Очас	0.9540796
усеченный кубооктаэдр (большой ромбокубооктаэдр)	tr {4,3}				4.6.8	26	12 квадратов 8 шестиугольников 6 восьмиугольников	72	48	41.798990	Очас	0.9431657
курносый куб (курносый кубооктаэдр)	sr {4,3}				3.3.3.3.4	38	32 треугольника 6 квадратов	60	24	7.889295	О	0.9651814
икосододекаэдр	г {5,3}				3.5.3.5	32	20 треугольников 12 пятиугольники	60	30	13.835526	ячас	0.9510243
усеченный додекаэдр	т {5,3}				3.10.10	32	20 треугольников 12 декагоны	90	60	85.039665	ячас	0.9260125
усеченный икосаэдр	т {3,5}				5.6.6	32	12 пятиугольников 20 шестиугольников	90	60	55.287731	ячас	0.9666219
ромбикосододекаэдр (малый ромбикосододекаэдр)	рр {5,3}				3.4.5.4	62	20 треугольников 30 квадратов 12 пятиугольников	120	60	41.615324	ячас	0.9792370
усеченный икосододекаэдр (большой ромбоикосододекаэдр)	tr {5,3}				4.6.10	62	30 квадратов 20 шестиугольников 12 декагонов	180	120	206.803399	ячас	0.9703127
курносый додекаэдр (курносый икосододекаэдр)	ср {5,3}				3.3.3.3.5	92	80 треугольников 12 пятиугольников	150	60	37.616650	я	0.9820114

Некоторые определения полуправильный многогранник включить еще одну цифру, удлиненная квадратная гиробикупола или «псевдоромбокубооктаэдр».^[3]

Характеристики

Количество вершин 720 ° деленное на вершину угловой дефект.

Кубооктаэдр и икосододекаэдр однотонный и называются квазирегулярный.

В двойники архимедовых тел называют Каталонские твердые вещества. Вместе с бипирамиды и трапецоэдры, эти мундир тела с правильными вершинами.

Хиральность

Курносый куб и курносый додекаэдр известны как хиральный, так как они бывают левосторонней (лат. левоморф или левоморф) и правосторонней формы (лат. декстроморф). Когда что-то появляется в нескольких формах, которые являются трехмерными зеркальное изображение эти формы можно назвать энантиоморфами. (Эта номенклатура также используется для форм некоторых химические соединения.)

Построение архимедовых тел

Архимедовы тела можно построить как позиции генератора в калейдоскопе.

Различные архимедовы и платоновы тела могут быть связаны друг с другом с помощью нескольких общих конструкций. Начиная с платонического тела, усечение предполагает обрезку углов. Для сохранения симметрии разрез выполняется в плоскости, перпендикулярной линии, соединяющей угол с центром многогранника, и одинаков для всех углов. В зависимости от того, насколько усечено (см. Таблицу ниже), могут быть созданы разные Платоновы и Архимедовы (и другие) твердые тела. Если усечение достаточно глубокое, так что каждая пара граней из соседних вершин имеет ровно одну точку, это называется исправлением. An расширение, или же песня, включает в себя перемещение каждой грани от центра (на такое же расстояние, чтобы сохранить симметрию Платонова тела) и взятие выпуклой оболочки. Расширение со скручиванием также включает поворот граней, таким образом, каждый прямоугольник, соответствующий ребру, разбивается на два треугольника по одной из диагоналей прямоугольника. Последняя конструкция, которую мы здесь используем, - это усечение углов и краев. Игнорируя масштабирование, расширение также можно рассматривать как исправление исправления. Точно так же обрезание можно рассматривать как усечение исправления.

Построение архимедовых тел

Симметрия		Тетраэдр	Восьмигранный		Икосаэдр
Стартовый твердый Операция	Символ {p, q}	Тетраэдр {3,3}	Куб {4,3}	Октаэдр {3,4}	Додекаэдр {5,3}	Икосаэдр {3,5}
Усечение (т)	т {р, д}	усеченный тетраэдр	усеченный куб	усеченный октаэдр	усеченный додекаэдр	усеченный икосаэдр
Исправление (р) Амбо (а)	г {р, д}	тетратраэдр (октаэдр)	кубооктаэдр		икосододекаэдр
Bitruncation (2т) Двойной кис (дк)	2t {p, q}	усеченный тетраэдр	усеченный октаэдр	усеченный куб	усеченный икосаэдр	усеченный додекаэдр
Биректификация (2р) Двойной (г)	2r {p, q}	тетраэдр	октаэдр	куб	икосаэдр	додекаэдр
песня (рр) Расширение (е)	рр {р, q}	ромбитратраэдр (кубооктаэдр)	ромбокубооктаэдр		ромбикосододекаэдр
Курносый ректификованный (SR) Курносый (s)	sr {p, q}	курносый тетратетраэдр (икосаэдр)	курносый кубооктаэдр		курносый икосододекаэдр
Cantitruncation (тр) Скос (b)	tr {p, q}	усеченный тетратетраэдр (усеченный октаэдр)	усеченный кубооктаэдр		усеченный икосододекаэдр

Обратите внимание на двойственность между кубом и октаэдром, а также между додекаэдром и икосаэдром. Кроме того, частично из-за того, что тетраэдр самодвойственен, только одно архимедово твердое тело имеет не более тетраэдрической симметрии. (Все Платоновы тела обладают как минимум тетраэдрической симметрией, поскольку тетраэдрическая симметрия является операцией симметрии (т.е. включена в) октаэдрической и изоэдрической симметрий, что демонстрируется тем фактом, что октаэдр можно рассматривать как выпрямленный тетраэдр, а икосаэдр может использоваться как курносый тетраэдр.)

Смотрите также

• Апериодическая мозаика
• Архимедов граф
• Икосаэдрические близнецы
• Список равномерных многогранников
• Куб принца Руперта # Обобщения
• Квазикристалл
• Правильный многогранник
• Полуправильный многогранник
• Тороидальный многогранник
• Равномерный многогранник

Цитаты

Общие ссылки

• Грюнбаум, Бранко (2009), «Постоянная ошибка», Elemente der Mathematik, 64 (3): 89–101, Дои:10.4171 / EM / 120, МИСТЕР  2520469. Перепечатано в Pitici, Mircea, ed. (2011), Лучшая работа по математике 2010 г., Princeton University Press, стр. 18–31..
• Джаятилаке, Удая (март 2005 г.). «Вычисления на правильных многогранниках с гранями и вершинами». Математический вестник. 89 (514): 76–81..
• Малькевич, Иосиф (1988), «Вехи истории многогранников», в Сенешаль, М.; Флек, Г. (ред.), Формирование пространства: многогранный подход, Boston: Birkhäuser, стр. 80–92..
• Пью, Энтони (1976). Многогранники: визуальный подход. Калифорния: Калифорнийский университет Press в Беркли. ISBN  0-520-03056-7. Глава 2
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN  0-486-23729-X. (Раздел 3-9)
• Шрайбер, Питер; Фишер, Гизела; Стернат, Мария Луиза (2008). «Новый свет на повторное открытие архимедовых тел в эпоху Возрождения». Архив истории точных наук. 62 (4): 457–467. Дои:10.1007 / s00407-008-0024-z. ISSN  0003-9519..

внешняя ссылка

• Вайсштейн, Эрик В. «Архимедово твердое тело». MathWorld.
• Архимедовы тела к Эрик В. Вайсштейн, Вольфрам Демонстрационный проект.
• Бумажные модели архимедовых тел и каталонских тел
• Свободные бумажные модели (сети) архимедовых тел
• Равномерные многогранники доктор Р. Мэдер
• Архимедовы тела в Visual Polyhedra Дэвида И. Маккуи
• Многогранники виртуальной реальности, Энциклопедия многогранников Джордж У. Харт
• Предпоследнее Модульное Оригами Джеймс С. Планк
• Интерактивные 3D-многогранники в Java
• Средство просмотра твердых тел представляет собой интерактивную программу просмотра трехмерных многогранников, которая позволяет сохранять модель в формате svg, stl или obj.
• Стелла: многогранник-навигатор: Программное обеспечение, используемое для создания многих изображений на этой странице.
• Бумажные модели архимедовых (и других) многогранников