Triacontatetragon - Triacontatetragon - Wikipedia
| Обычный триаконтатетрагон | |
|---|---|
 Обычный триаконтатрагон | |
| Тип | Правильный многоугольник |
| Края и вершины | 34 |
| Символ Шлефли | {34}, т {17} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D34), заказ 2 × 34 |
| Внутренний угол (градусы ) | 169.412° |
| Двойной многоугольник | Себя |
| Характеристики | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
В геометрия, а триаконтатрагон или же триаконтакайтракон это тридцать четыре стороны многоугольник или 34-угольник.[1] Сумма внутренних углов любого триаконтатетрагона составляет 5760 градусов.
Обычный триаконтатетрагон
А обычный триаконтатрагон представлен Символ Шлефли {34} а также может быть выполнен в виде усеченный 17-угольник, t {17}, который чередует два типа ребер.
Один внутренний угол в обычном триаконтатетрагоне равен (2880/17) °, что означает, что один внешний угол будет (180/17) °.
В площадь штатного триаконтатрагона есть (с т = длина кромки)
и это inradius является
Фактор является корнем уравнение .
В по окружности обычного триаконтатрагона есть
Поскольку 34 = 2 × 17 и 17 - это Ферма Прайм, обычный триаконтатрагон конструктивный используя компас и линейка.[2][3][4] Как усеченный 17-угольник, его можно построить с помощью ребраделение пополам правильного 17-угольника. Это означает, что значения и могут быть выражены вложенными радикалами.
Симметрия
В обычный триаконтатрагон имеет Dih34 симметрия, порядок 68. Существует 3 диэдральных симметрии подгруппы: Dih17, Ди2, и Dih1, и 4 циклическая группа симметрии: Z34, Z17, Z2, а Z1.
Эти 8 симметрий можно увидеть в 10 различных симметриях на икосидигоне, большее число, потому что линии отражений могут проходить либо через вершины, либо через ребра. Джон Конвей помечает их буквой и групповым порядком.[5] Полная симметрия регулярной формы помечена r68 и симметрия не помечена а1. Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров), и я когда линии отражения проходят через ребра и вершины. Циклические симметрии n обозначаются как грамм для их приказов центрального вращения.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g34 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.
Неправильные триаконтатегоны высшей симметрии - это d34, изогональный triacontatetragon, состоящий из семнадцати зеркал, которые могут чередовать длинные и короткие края, и стр. 34, изотоксальный triacontatetragon, построенный с равной длиной ребер, но вершинами, чередующимися под двумя разными внутренними углами. Эти две формы двойники друг друга и имеют половину порядка симметрии обычного триаконтатетрагона.
Рассечение

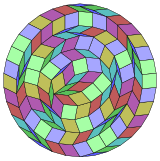
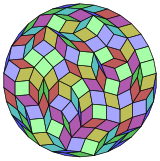
Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.[6]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для обычный триаконтатрагон, м= 17, его можно разделить на 136: 8 наборов по 17 ромбов. Это разложение основано на Многоугольник Петри проекция 17-куб.
 |  |  |  |  |
Триаконтатетраграмма
Триаконтатетраграмма - это 34-сторонняя звездный многоугольник. Есть семь обычных форм, которые дает Символы Шлефли {34/3}, {34/5}, {34/7}, {34/9}, {34/11}, {34/13} и {34/15}, и девять соединений звездные фигуры с тем же конфигурация вершины.
 {34/3} |  {34/5} |  {34/7} |  {34/9} |  {34/11} |  {34/13} |  {34/15} |
Много изогональный триаконтатетраграммы также могут быть построены как более глубокие усечения регулярных гептадекагон {17} и гептадекаграммы {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7} и {17/8}. Они также создают восемь квазиусечений: t {17/9} = {34/9}, t {17/10} = {34/10}, t {17/11} = {34/11}, t {17/12 } = {34/12}, t {17/13} = {34/13}, t {17/14} = {34/14}, t {17/15} = {34/15} и t { 17/16} = {34/16}. Некоторые изогональные триаконтатетраграммы изображены ниже в виде усеченной последовательности с конечными точками t {17} = {34} и t {17/16} = {34/16}.[7]
 t {17} = {34} |  |  |  |  |  |  |  |  т {17/16} = {34/16} |
Рекомендации
- ^ "Спросите доктора Матема: наименование многоугольников и многогранников". mathforum.org. Получено 2017-09-05.
- ^ В., Вайсштейн, Эрик. «Конструируемый многоугольник». mathworld.wolfram.com. Получено 2017-09-01.
- ^ Чепмелл, К. Х. (1913-03-01). «Построение правильного многоугольника из 34 сторон» (PDF). Mathematische Annalen. 74 (1): 150–151. Дои:10.1007 / bf01455349. ISSN 0025-5831.
- ^ Белый, Чарльз Эдгар (1913). Теория неприводимых случаев уравнений и ее приложения в алгебре, геометрии и тригонометрии. п. 79.
- ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
- ^ Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
- ^ Светлая сторона математики: Материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум







