Тороидальный многогранник - Toroidal polyhedron
В геометрия, а тороидальный многогранник это многогранник который также является тороид (а грамм-отвернутый тор ), иметь топологический род 1 или больше. Известные примеры включают Császár и Многогранники Силасси.
Варианты определения
Тороидальные многогранники определяются как совокупности полигоны которые встречаются на своих краях и вершинах, образуя многообразие как они это делают. То есть каждое ребро должно быть разделено ровно на два многоугольника, а связь каждой вершины должен быть один цикл, который чередуется между ребрами и многоугольниками, которые встречаются в этой вершине. Для тороидальных многогранников это многообразие является ориентируемая поверхность.[1] Некоторые авторы ограничивают словосочетание «тороидальные многогранники» более конкретным обозначением многогранников, топологически эквивалентных (род 1) тор.[2]
В этой области важно различать встроенный тороидальные многогранники, грани которых являются плоскими многоугольниками в трехмерном пространстве. Евклидово пространство которые не перекрещиваются друг с другом, от абстрактные многогранники, топологические поверхности без заданной геометрической реализации.[3] Промежуточным звеном между этими двумя крайностями являются многогранники, образованные геометрическими многоугольниками или звездные многоугольники в евклидовом пространстве, которым разрешено пересекать друг друга.
Во всех этих случаях тороидальный характер многогранника подтверждается его ориентируемостью и его ориентацией. Эйлерова характеристика быть отрицательным. Эйлерова характеристика обобщается на V − E + F = 2 − 2N, куда N количество отверстий.
Многогранники Часара и Силасси
 Интерактивная модель многогранника Сзиласси с каждой гранью разного цвета. В изображение SVG, переместите мышь влево и вправо, чтобы повернуть его.[4] |  Интерактивная модель многогранника Часара. В изображение SVG, переместите мышь, чтобы повернуть его.[5] |
Два из самых простых возможных вложенных тороидальных многогранников - это многогранники Часара и Силасси.
В Многогранник Часара представляет собой семивершинный тороидальный многогранник с 21 ребром и 14 треугольными гранями.[6] Это и тетраэдр являются единственными известными многогранниками, в которых каждый возможный отрезок, соединяющий две вершины, образует ребро многогранника.[7] Его двойственный, Многогранник Силасси, имеет семь шестиугольных граней, которые примыкают друг к другу,[8] следовательно, обеспечивая существование половины теорема что максимальное количество цветов, необходимое для отображения на торе (первого рода), равно семи.[9]
Многогранник Часара имеет наименьшее возможное количество вершин любого вложенного тороидального многогранника, а многогранник Силасси имеет наименьшее возможное количество граней любого вложенного тороидального многогранника.
Тороиды Стюарта
Особая категория тороидальных многогранников строится исключительно правильный многоугольник грани, без пересечений и с дополнительным ограничением, что смежные грани не могут лежать в одной плоскости друг с другом. Они называются Тороиды Стюарта,[10] названный в честь Бонни Стюарт, которые интенсивно их изучили.[11] Они аналогичны Твердые тела Джонсона в случае выпуклые многогранники; однако, в отличие от тел Джонсона, тороидов Стюарта бесконечно много.[12] К ним относятся также тороидальные дельтаэдры, многогранники, все грани которых представляют собой равносторонние треугольники.
Ограниченный класс тороидов Стюарта, также определенный Стюартом, - это квазивыпуклые тороидальные многогранники. Это тороиды Стюарта, которые включают в себя все края их выпуклые оболочки. Для такого многогранника каждая грань выпуклой оболочки либо лежит на поверхности тороида, либо представляет собой многоугольник, все ребра которого лежат на поверхности тороида.[13]
| Род | 1 | 1 |
|---|---|---|
| Изображение | 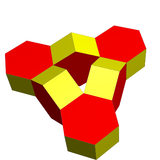 | 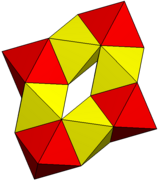 |
| Многогранники | 6 шестиугольные призмы | 8 октаэдры |
| Вершины | 48 | 24 |
| Края | 84 | 72 |
| Лица | 36 | 48 |
| Род | 1 | 3 | 11 | 3 | 5 | 7 | 11 | |
|---|---|---|---|---|---|---|---|---|
| Изображение |  |  |  |  |  |  |  | 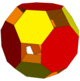 |
| Многогранники | 4 квадратные купола 8 тетраэдры | 6 треугольные купола 6 квадратные пирамиды | 4 треугольные купола 6 квадратные пирамиды | 24 треугольные призмы 6 квадратные пирамиды 8 тетраэдры | 6 квадратные купола 4 треугольные купола 12 кубики | 8 треугольные купола 12 кубики | 6 квадратные купола 12 кубики | 6 квадратные купола 8 треугольные купола |
| Выпуклый корпус | усеченный куб | усеченный октаэдр | усеченный октаэдр | расширенный кубооктаэдр | усеченный кубооктаэдр | усеченный кубооктаэдр | усеченный кубооктаэдр | усеченный кубооктаэдр |
| Вершины | 32 | 30 | 30 | 62 | 72 | 72 | 72 | 72 |
| Края | 64 | 60 | 72 | 168 | 144 | 168 | 168 | 168 |
| Лица | 32 | 30 | 38 | 86 | 68 | 88 | 84 | 76 |
Самопересекающиеся многогранники
 Октагемиоктаэдр |  Малый кубокубооктаэдр |  Большой додекаэдр |
Многогранник, образованный системой пересекающихся многоугольников, соответствует абстрактному топологическому многообразию, образованному его многоугольниками и их системой общих ребер и вершин, и род многогранника может быть определен из этого абстрактного многообразия. Примеры включают род-1 октагемиоктаэдр, род-3 малый кубокубооктаэдр, а род-4 большой додекаэдр.
Коронные многогранники

А корона многогранник или же стефаноид тороидальный многогранник, который также благородный, будучи обоими изогональный (равные вершины) и равногранный (равные лица). Коронные многогранники самопересекающиеся и топологически самодвойственный.[14]
Смотрите также
- Проективный многогранник
- Косой апейроэдр (бесконечный косой многогранник)
- Сферический многогранник
- Тороидальный граф
Рекомендации
- ^ Уайтли (1979); Стюарт (1980), п. 15.
- ^ Уэббер, Уильям Т. (1997), "Одноэдральные идемвалентные многогранники, которые являются тороидами", Geometriae Dedicata, 67 (1): 31–44, Дои:10.1023 / А: 1004997029852, МИСТЕР 1468859.
- ^ Уайтли, Уолтер (1979), «Реализуемость многогранников» (PDF), Структурная топология (1): 46–58, 73, МИСТЕР 0621628.
- ^ Бранко Грюнбаум, Лайош Силасси, Геометрические реализации специальных тороидальных комплексов., Вклад в дискретную математику, Том 4, номер 1, страницы 21-39, ISSN 1715-0868
- ^ Акос Часар, Многогранник без диагоналей., Институт Бойяи, Сегедский университет, 1949 г.
- ^ Часар, А. (1949), «Многогранник без диагоналей», Acta Sci. Математика. Сегед, 13: 140–142.
- ^ Циглер, Гюнтер М. (2008), «Полиэдрические поверхности высокого рода», Бобенко, А. И .; Schröder, P .; Салливан, Дж. М.; Зиглер, Г. М. (ред.), Дискретная дифференциальная геометрия, Обервольфахские семинары, 38, Springer-Verlag, стр. 191–213, arXiv:math.MG/0412093, Дои:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7.
- ^ Силасси, Лайош (1986), «Штатные тороиды» (PDF), Структурная топология, 13: 69–80[постоянная мертвая ссылка ].
- ^ Хивуд, П. Дж. (1890), «Теоремы о раскраске карт», Ежеквартально J. Math. Oxford Ser., 24: 322–339
- ^ Уэбб, Роберт (2000), «Стелла: навигатор по многограннику», Симметрия: культура и наука, 11 (1–4): 231–268, МИСТЕР 2001419.
- ^ Стюарт, Б. М. (1980), Приключения среди тороидов: исследование ориентированных многогранников с правильными гранями (2-е изд.), Б. М. Стюарт, ISBN 978-0-686-11936-4.
- ^ Стюарт (1980), п. 15.
- ^ Стюарт (1980), "Квазивыпуклость и слабая квазивыпуклость", стр. 76–79.
- ^ Грюнбаум, Бранко (1994), «Многогранники с полыми гранями», Многогранники: абстрактные, выпуклые и вычислительные, Серия C НАТО ASI: Математические и физические серии, 440, Kluwer Academic Publishers, стр. 43–70, Дои:10.1007/978-94-011-0924-6_3. См. В частности п. 60.

