Список конечных групп сферической симметрии - List of finite spherical symmetry groups
 Инволюционная симметрия Cs, (*) [ ] = |  Циклическая симметрия CNV, (* nn) [n] = |  Двугранная симметрия Dнэ, (* n22) [n, 2] = | |
| Группа полиэдров, [n, 3], (* n32) | |||
|---|---|---|---|
 Тетраэдрическая симметрия Тd, (*332) [3,3] = |  Октаэдрическая симметрия Очас, (*432) [4,3] = |  Икосаэдрическая симметрия ячас, (*532) [5,3] = | |
Конечные группы сферической симметрии также называют группы точек в трех измерениях. Существует пять фундаментальных классов симметрии, которые имеют треугольные фундаментальные области: двугранный, циклический, четырехгранный, восьмигранный, и икосаэдр симметрия.
В этой статье перечислены группы по Обозначение Шенфлиса, Обозначение Кокстера,[1] орбифолдная запись,[2] и заказ. Джон Конвей использует вариант нотации Шенфлиса, основанный на группах ' кватернион алгебраическая структура, обозначенная одной или двумя прописными буквами и целыми индексами. Порядок групп определяется как нижний индекс, если порядок не удваивается для символов с префиксом плюс или минус, "±", что подразумевает центральная инверсия.[3]
Обозначения Германа – Могена (Международное обозначение) также дается. В кристаллография группы, всего 32, представляют собой подмножество с порядками элементов 2, 3, 4 и 6.[4]
Инволюционная симметрия
Есть четыре инволюционный группы: нет симметрии (C1), симметрия отражения (Cs), 2-кратная вращательная симметрия (C2) и центральный точечная симметрия (Cя).
| Intl | Гео [5] | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 11 | C1 | C1 | ][ [ ]+ | 1 |  |
| 2 | 2 | 22 | D1 = C2 | D2 = C2 | [2]+ | 2 |  |
| 1 | 22 | × | Cя = S2 | CC2 | [2+,2+] | 2 | 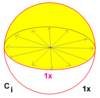 |
| 2 = м | 1 | * | Cs = C1v = C1 час | ± C1 = CD2 | [ ] | 2 |  |
Циклическая симметрия
Есть четыре бесконечных циклическая симметрия семьи, с п = 2 или выше. (п может быть 1 как особый случай, поскольку нет симметрии)
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 4 | 42 | 2× | S4 | CC4 | [2+,4+] | 4 |  |
| 2 / м | 22 | 2* | C2ч = D1д | ± C2 = ± D2 | [2,2+] [2+,2] | 4 | 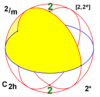 |
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 2 3 4 5 6 п | 2 3 4 5 6 п | 22 33 44 55 66 nn | C2 C3 C4 C5 C6 Cп | C2 C3 C4 C5 C6 Cп | [2]+ [3]+ [4]+ [5]+ [6]+ [n]+ | 2 3 4 5 6 п |  |
| 2мм 3м 4мм 5м 6мм нм (n нечетное) nmm (n четное) | 2 3 4 5 6 п | *22 *33 *44 *55 *66 * нн | C2v C3в C4в C5в C6v CNV | CD4 CD6 CD8 CD10 CD12 CD2n | [2] [3] [4] [5] [6] [n] | 4 6 8 10 12 2n |  |
| 3 8 5 12 - | 62 82 10.2 12.2 2н.2 | 3× 4× 5× 6× п × | S6 S8 S10 S12 S2n | ± C3 CC8 ± C5 CC12 CC2n / ± Cп | [2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+, 2н+] | 6 8 10 12 2n |  |
| 3 / м =6 4 / м 5 / м =10 6 / м н / м | 32 42 52 62 п2 | 3* 4* 5* 6* п * | C3ч C4ч C5ч C6ч Cнэ | CC6 ± C4 CC10 ± C6 ± Cп / CC2n | [2,3+] [2,4+] [2,5+] [2,6+] [2, n+] | 6 8 10 12 2n |  |
Двугранная симметрия
Есть три бесконечных двугранная симметрия семьи, с п = 2 или выше (п может быть 1 как особый случай).
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 222 | 2.2 | 222 | D2 | D4 | [2,2]+ | 4 |  |
| 42м | 42 | 2*2 | D2d | DD8 | [2+,4] | 8 |  |
| М-м-м | 22 | *222 | D2ч | ± D4 | [2,2] | 8 |  |
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 32 422 52 622 | 3.2 4.2 5.2 6.2 п.2 | 223 224 225 226 22n | D3 D4 D5 D6 Dп | D6 D8 D10 D12 D2n | [2,3]+ [2,4]+ [2,5]+ [2,6]+ [2, n]+ | 6 8 10 12 2n | 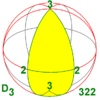 |
| 3м 82м 5м 120,2 м | 62 82 10.2 12.2 п2 | 2*3 2*4 2*5 2*6 2 * п | D3D D4d D5d D6d Dnd | ± D6 DD16 ± D10 DD24 DD4n / ± D2n | [2+,6] [2+,8] [2+,10] [2+,12] [2+, 2н] | 12 16 20 24 4n |  |
| 6m2 4 / ммм 10m2 6 / ммм | 32 42 52 62 n2 | *223 *224 *225 *226 * 22n | D3ч D4ч D5ч D6ч Dнэ | DD12 ± D8 DD20 ± D12 ± D2n / ДД4n | [2,3] [2,4] [2,5] [2,6] [2, n] | 12 16 20 24 4n |  |
Полиэдральная симметрия
Есть три типа многогранная симметрия: тетраэдрическая симметрия, октаэдрическая симметрия, и икосаэдрическая симметрия, названный в честь треугольника правильные многогранники с этими симметриями.
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 23 | 3.3 | 332 | Т | Т | [3,3]+ = [4,3+]+ | 12 |  |
| м3 | 43 | 3*2 | Тчас | ± Т | [4,3+] | 24 |  |
| 43м | 33 | *332 | Тd | К | [3,3] = [1+,4,3] | 24 |  |
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 432 | 4.3 | 432 | О | О | [4,3]+ = [[3,3]]+ | 24 | 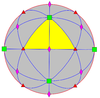 |
| м3м | 43 | *432 | Очас | ± O | [4,3] = [[3,3]] | 48 |  |
| Intl | Гео | Сфера. | Schön. | Против. | Кокс. | Ord. | Фонд. домен |
|---|---|---|---|---|---|---|---|
| 532 | 5.3 | 532 | я | я | [5,3]+ | 60 | 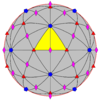 |
| 532 / м | 53 | *532 | ячас | ± я | [5,3] | 120 |  |
Смотрите также
- Кристаллографическая точечная группа
- Группа треугольников
- Список плоских групп симметрии
- Группы точек в двух измерениях
Примечания
Рекомендации
- Питер Р. Кромвель, Многогранники (1997), Приложение I
- Пески, Дональд Э. (1993). «Кристаллические системы и геометрия». Введение в кристаллографию. Минеола, Нью-Йорк: Dover Publications, Inc. стр. 165. ISBN 0-486-67839-3.
- О кватернионах и октонионах, 2003, Джон Хортон Конвей и Дерек А. Смит ISBN 978-1-56881-134-5
- Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5
- Калейдоскопы: избранные произведения H.S.M. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559–591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3–45]
- N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, Таблица 11.4 Конечные группы изометрий в трехмерном пространстве
