Фаска (геометрия) - Chamfer (geometry)

Куб без фаски, слегка скошенный и с фаской

Исторический кристаллографический модели платоновых тел со слегка скошенными кромками

В геометрия, снятие фаски или же обрезка края - топологический оператор, преобразующий один многогранник в другой. Это похоже на расширение, перемещая грани в стороны и наружу, но также сохраняет исходные вершины. Для многогранников эта операция добавляет новую шестиугольную грань вместо каждого исходного ребра.

В Обозначения многогранника Конвея он представлен буквой c. Многогранник с е края будут иметь скошенную форму, содержащую 2е новые вершины, 3е новые края и е новые шестиугольные грани.

Платоновы тела с фаской

В главах ниже фаски пяти Платоновы тела описаны подробно. Каждый показан в версии с краями одинаковой длины и в канонической версии, где все края соприкасаются одинаково. средняя сфера. (Они выглядят заметно иначе только для твердых тел, содержащих треугольники.) двойники двойственны каноническим версиям.

Семя	{3,3}	{4,3}	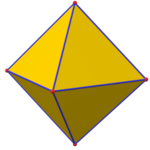{3,4}	{5,3}	{3,5}
Скошенный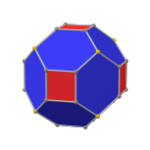

Тетраэдр с фаской

Тетраэдр с фаской
(с равной длиной кромки)
Обозначение Конвея	cT
Многогранник Гольдберга	GPIII(2,0) = {3+,3}2,0
Лица	4 треугольники 6 шестиугольники
Края	24 (2 типа)
Вершины	16 (2 типа)
Конфигурация вершины	(12) 3.6.6 (4) 6.6.6
Группа симметрии	Тетраэдр (Тd)
Двойной многогранник	Альтернативно-триакис-тетратетраэдр
Характеристики	выпуклый, равносторонний с лицом
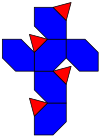сеть

В скошенный тетраэдр (или же альтернативный усеченный куб) это выпуклый многогранник построенный как попеременно усеченный куб или операция снятия фаски на тетраэдре, заменяя его 6 ребер шестиугольниками.

Это Многогранник Гольдберга грамм_III(2,0), содержащий треугольные и шестиугольные грани.

В усеченный тетраэдр выглядит похожим, но его шестиугольники соответствуют 4 вершинам тетраэдра, а не 6 ребрам.

Тетраэдрические фаски и связанные с ними твердые тела

тетраэдр с фаской (канонический)	двойственный тетраэтраэдру	тетраэдр с фаской (канонический)
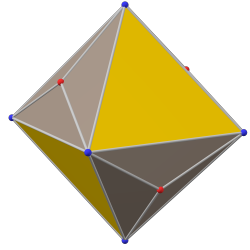альтернативный триакис тетратраэдр	тетратраэдр	альтернативный триакис тетратраэдр

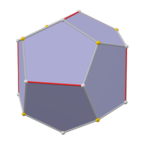
Куб с фаской

Куб с фаской
(с равной длиной кромки)
Обозначение Конвея	cC = t4daC
Многогранник Гольдберга	GPIV(2,0) = {4+,3}2,0
Лица	6 квадраты 12 шестиугольники
Края	48 (2 типа)
Вершины	32 (2 типа)
Конфигурация вершины	(24) 4.6.6 (8) 6.6.6
Симметрия	Очас, [4,3], (*432) Тчас, [4,3+], (3*2)
Двойной многогранник	Кубооктаэдр Тетракиса
Характеристики	выпуклый, равносторонний с лицом
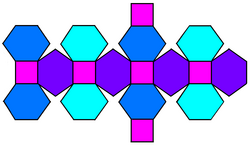сеть

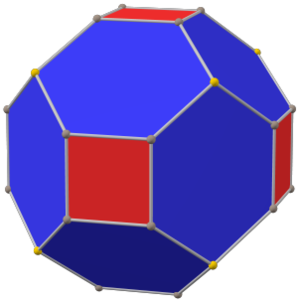
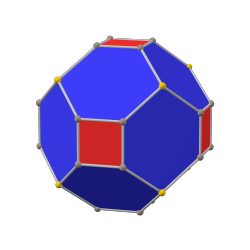
В куб с фаской это выпуклый многогранник с 32 вершинами, 48 ребрами и 18 гранями: 12 шестиугольников и 6 квадратов. Он выполнен в виде фаски куб. Квадраты уменьшаются в размере, и вместо всех исходных краев добавляются новые шестиугольные грани. Его двойным является тетракис кубооктаэдр.

Его также неточно называют усеченный ромбический додекаэдр, хотя это название скорее предполагает ромбокубооктаэдр. Его точнее можно назвать тетраусеченный ромбический додекаэдр потому что только вершины порядка 4 усекаются.

Шестиугольные грани равносторонний но нет обычный. Они образованы усеченным ромбом, имеют 2 внутренних угла около 109,47 °. ${ displaystyle cos ^ {- 1} (- { frac {1} {3}})}$ и 4 внутренних угла около 125,26 °, в то время как правильный шестиугольник будет иметь все углы 120 °.

Поскольку все его грани имеют четное количество сторон с симметрией поворота на 180 °, это зоноэдр. Это также Многогранник Гольдберга GP_IV(2,0) или {4 +, 3}_2,0, содержащий квадратные и шестиугольные грани.

В куб с фаской это Сумма Минковского ромбического додекаэдра и куба со стороной 1, когда восемь вершин ромбического додекаэдра находятся в ${ Displaystyle ( pm 1, pm 1, pm 1)}$ и его шесть вершин находятся в перестановках ${ displaystyle ( pm { sqrt {3}}, 0,0)}$.

А топологический эквивалент с пиритоэдрическая симметрия и прямоугольные грани могут быть построены путем снятия фаски с осевых кромок пиритоэдр. Это происходит в пирит кристаллы.

Пиритоэдр и усечение его оси

Исторические кристаллографические модели

В усеченный октаэдр выглядит похоже, но его шестиугольники соответствуют 8 вершинам куба, а не его 12 ребрам.

Октаэдрические фаски и связанные с ними твердые тела

куб с фаской (канонический)	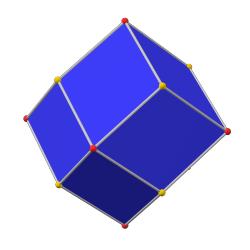ромбический додекаэдр	октаэдр с фаской (канонический)
тетракис кубооктаэдр	кубооктаэдр	триакис кубооктаэдр

Октаэдр с фаской

Октаэдр с фаской
(с равной длиной кромки)
Обозначение Конвея	cO = t3daO
Лица	8 треугольники 12 шестиугольники
Края	48 (2 типа)
Вершины	30 (2 типа)
Конфигурация вершины	(24) 3.6.6 (6) 6.6.6
Симметрия	Очас, [4,3], (*432)
Двойной многогранник	Кубооктаэдр Триаки
Характеристики	выпуклый

В геометрия, то октаэдр с фаской это выпуклый многогранник построенный из ромбический додекаэдр к усечение 8 (порядок 3) вершин.

Его также можно назвать усеченный ромбический додекаэдр, обрезание вершин порядка 3 ромбический додекаэдр.

8 вершин обрезаются так, чтобы все ребра были равной длины. Оригинальный 12 ромбический грани становятся плоскими шестиугольниками, а усеченные вершины становятся треугольниками.

Шестиугольные грани равносторонний но нет обычный.

Исторические рисунки ромбического кубооктаэдра и октаэдра со скошенной фаской

Исторические модели кубооктаэдра триаки и октаэдра со скошенной фаской

Додекаэдр с фаской

Додекаэдр с фаской
(с равной длиной кромки)
Обозначение Конвея	cD] = t5daD = dk5aD
Многогранник Гольдберга	граммV(2,0) = {5+,3}2,0
Фуллерен	C80[1]
Лица	12 пятиугольники 30 шестиугольники
Края	120 (2 типа)
Вершины	80 (2 типа)
Конфигурация вершины	(60) 5.6.6 (20) 6.6.6
Группа симметрии	Икосаэдр (ячас)
Двойной многогранник	Пентакис икосододекаэдр
Характеристики	выпуклый, равносторонний с лицом

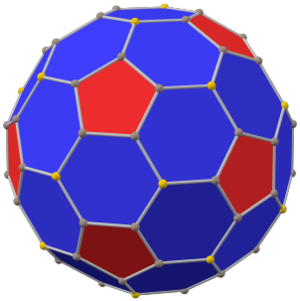
В додекаэдр с фаской это выпуклый многогранник с 80 вершинами, 120 ребрами и 42 гранями: 30 шестиугольников и 12 пятиугольников. Он выполнен в виде фаски правильный додекаэдр. Пятиугольники уменьшаются в размере, и вместо всех исходных краев добавляются новые шестиугольные грани. Его двойным является пентакис икосододекаэдр.

Его также неточно называют усеченный ромбический триаконтаэдр, хотя это название скорее предполагает ромбикосододекаэдр. Точнее его можно назвать пятиусеченный ромбический триаконтаэдр потому что только вершины порядка 5 усекаются.

В усеченный икосаэдр выглядит похоже, но его шестиугольники соответствуют 20 вершинам додекаэдра, а не его 30 ребрам.

Икосаэдрические фаски и связанные с ними твердые тела

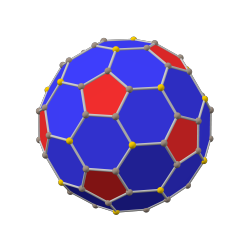додекаэдр с фаской (канонический)	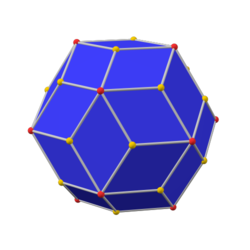ромбический триаконтаэдр	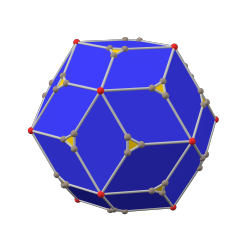икосаэдр с фаской (канонический)
пентакис икосододекаэдр	икосододекаэдр	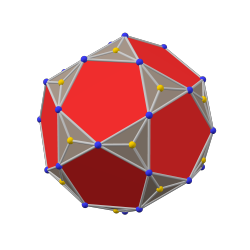триакис икосододекаэдр

Икосаэдр с фаской

Икосаэдр с фаской
(с равной длиной кромки)
Обозначение Конвея	cI = t3daI
Лица	20 треугольники 30 шестиугольники
Края	120 (2 типа)
Вершины	72 (2 типа)
Конфигурация вершины	(24) 3.6.6 (12) 6.6.6
Симметрия	ячас, [5,3], (*532)
Двойной многогранник	триакис икосододекаэдр
Характеристики	выпуклый

В геометрия, то икосаэдр с фаской это выпуклый многогранник построенный из ромбический триаконтаэдр к усечение 20 вершин порядка 3. Шестиугольные грани можно сделать равносторонний но нет обычный.

Его также можно назвать усеченный ромбический триаконтаэдр, обрезание вершин порядка 3 ромбический триаконтаэдр.

Правильные плитки с фаской

Правильные и квазирегулярные мозаики с фаской

Квадратная плитка, Q {4,4}	Треугольная черепица, Δ {3,6}	Шестиугольная черепица, H {6,3}	Ромбиль, дач др {6,3}
cQ	cΔ	cH	cdaH

Связь с многогранниками Гольдберга

Операция снятия фаски, применяемая последовательно, создает постепенно увеличивающиеся многогранники с новыми шестиугольными гранями, заменяющими ребра из предыдущего. Оператор фаски преобразует GP (m, n) в GP (2m, 2n).

Правильный многогранник GP (1,0) создает Многогранники Гольдберга последовательность: GP (1,0), GP (2,0), GP (4,0), GP (8,0), GP (16,0) ...

	GP (1,0)	GP (2,0)	GP (4,0)	GP (8,0)	GP (16,0) ...
GPIV {4+,3}	C	cC	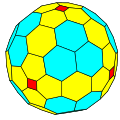ccC	cccC
GPV {5+,3}	D	CD	ccD	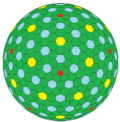cccD	ccccD
GPVI {6+,3}	ЧАС	cH	ccH	cccH	ccccH

В усеченный октаэдр или же усеченный икосаэдр, GP (1,1) создает последовательность Голдберга: GP (1,1), GP (2,2), GP (4,4), GP (8,8) ....

	GP (1,1)	GP (2,2)	GP (4,4) ...
GPIV {4+,3}	к	ctO	cctO
GPV {5+,3}	tI	ctI	cctI
GPVI {6+,3}	tH	ctH	cctH

А усеченный тетракис шестигранник или же пентакид додекаэдр, GP (3,0), создает последовательность Голдберга: GP (3,0), GP (6,0), GP (12,0) ...

	GP (3,0)	GP (6,0)	GP (12,0) ...
GPIV {4+,3}	tkC	ctkC	cctkC
GPV {5+,3}	tkD	ctkD	cctkD
GPVI {6+,3}	tkH	ctkH	cctkH

Многогранники с фаской и соты

Как и операция расширения, фаска может применяться к любому размеру. Для многоугольников он утроил количество вершин. Для полихоры новые ячейки создаются вокруг исходных краев. Ячейки представляют собой призмы, содержащие две копии исходной грани с пирамидами, увеличенными на сторонах призмы.

Смотрите также

• Обозначения многогранника Конвея
• Почти мисс Джонсон солид
• Cantellation (геометрия)

Рекомендации

• Гольдберг, Майкл (1937). «Класс мультисимметричных многогранников». Математический журнал Тохоку. 43: 104–108.
• Джозеф Д. Клинтон, Гипотеза Клинтона о равных центральных углах [1]
• Харт, Джордж (2012). «Многогранники Гольдберга». В Сенешаль, Марджори (ред.). Формирование пространства (2-е изд.). Springer. стр.125 –138. Дои:10.1007/978-0-387-92714-5_9. ISBN  978-0-387-92713-8.
• Харт, Джордж (18 июня 2013 г.). «Математические впечатления: многогранники Гольдберга». Саймонс Новости науки.
• Антуан Деза, Мишель Деза, Вячеслав Грищухин, Фуллерены и координационные многогранники против вложений полукуба, 1998 PDF [2] (стр. 72 Рис. 26. Тетраэдр с фаской)
• Deza, A .; Деза, М.; Гришухин, В. (1998), «Фуллерены и координационные многогранники против вложений полукуба», Дискретная математика, 192 (1): 41–80, Дои:10.1016 / S0012-365X (98) 00065-X, заархивировано из оригинал на 2007-02-06.

внешняя ссылка

• Тетраэдр с фаской
• Тела с фаской
• Обрезание вершин и ребер Платоновых и Архимедовых тел, приводящее к вершинно-транзитивным многогранникам Ливио Зефиро
• Генератор многогранников VRML (Обозначения многогранника Конвея )
  • VRML модель Куб с фаской
• 3.2.7. Систематическая нумерация для (C80-Ih) [5,6] фуллерен
• Фуллерен C80
  1. [3] (Число 7 -Ih)
  2. [4]
• Как сделать куб с фаской