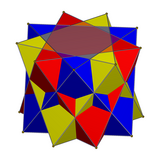
Соединение трех октаэдров - Compound of three octahedra
| Соединение трех октаэдров | |
|---|---|
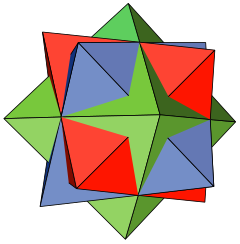 | |
| Многогранники | 3 правильные октаэдры |
| Лица | 24 равносторонние треугольники |
| Края | 36 |
| Вершины | 18 |
| Группа симметрии (Один цвет) | Очас, заказ 48 |
В математике соединение трех октаэдров или же октаэдр 3-соединение это полиэдрическое соединение сформирован из трех правильные октаэдры, все они имеют общий центр, но повернуты друг относительно друга. Хотя он и появился раньше в математической литературе, он был заново открыт и популяризирован М. К. Эшер, который использовал его в центральном изображении своей гравюры на дереве 1948 года. Звезды.
Строительство
Правильный октаэдр можно описать вокруг куба таким образом, чтобы восемь ребер двух противоположных квадратов куба лежали на восьми гранях октаэдра. Три октаэдра, образованные таким образом из трех пар противоположных кубических квадратов, образуют соединение трех октаэдров.[1] Восемь вершин куба совпадают с восемью точками соединения, в которых три ребра пересекаются.[2] Каждое из ребер октаэдра, которое участвует в этих тройных пересечениях, делится точкой пересечения в соотношении 1:√2.[2] Остальные края октаэдра попарно пересекают друг друга внутри соединения; их пересечения находятся в их серединах и образуют прямые углы.
Соединение трех октаэдров также может быть образовано из трех копий одного октаэдра путем поворота каждой копии на угол π/ 4 вокруг одного из трех оси симметрии проходящие через две противоположные вершины начального октаэдра.[3] Третья конструкция для того же соединения трех октаэдров выглядит как двойственный многогранник из соединение трех кубиков, один из однородные многогранники.
Шесть вершин одного из трех октаэдров могут быть заданы координатами (0, 0, ±2) и (±√2, ±√2, 0). Два других октаэдра имеют координаты, которые могут быть получены из этих координат путем обмена z координаты для Икс или же у координировать.[1][2]
Симметрии

Соединение трех октаэдров имеет одинаковые группа симметрии как одиночный октаэдр. равногранный дельтаэдр, что означает, что его грани представляют собой равносторонние треугольники и что он имеет симметрию, соединяющую все грани с другими гранями. Есть одно известное бесконечное семейство равногранных дельтаэдров и еще 36, которые не попадают в это семейство; соединение трех октаэдров - один из 36 спорадических примеров.[4] Однако его группа симметрии не переводит каждую вершину во все остальные вершины, поэтому сама она не является однородным составным многогранником.
Пересечение трех октаэдров есть выпуклый многогранник с 14 вершинами и 24 гранями, a тетракис шестигранник, образованный прикреплением низкого квадратная пирамида каждой грани центрального куба.[2] Таким образом, соединение можно рассматривать как звездчатость шестигранника тетракис. Другая форма тетракис-шестигранника, образованного более высокими пирамидами на каждой грани куба, невыпуклая, но имеет равносторонние треугольные грани, которые снова лежат на тех же плоскостях, что и грани трех октаэдров; это еще один из известных равногранных дельтаэдров. Третий равногранный дельтаэдр, разделяющий те же плоскости граней, соединение шести тетраэдров, может быть образован звездчатый каждая грань соединения трех октаэдров, чтобы сформировать три Stellae octangulae. Четвертый равногранный дельтаэдр с такими же плоскостями граней, также звездчатая форма соединения трех октаэдров, имеет ту же комбинаторную структуру, что и тетракис-гексаэдр, но с гранями куба, вдавленными внутрь в пересекающиеся пирамиды, а не прикрепляющими пирамиды к внешней стороне куба. .[4]
Куб, вокруг которого можно описать три октаэдра, имеет девять плоскостей симметрия отражения. Три из этих отражающих панелей проходят параллельно сторонам куба на полпути между двумя противоположными сторонами; остальные шесть проходят через куб по диагонали через четыре его вершины. Эти девять плоскостей совпадают с девятью экваториальными плоскостями трех октаэдров.[2]
История
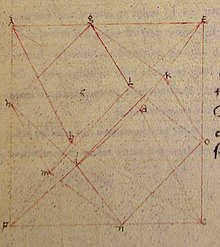
В рукописи XV века De quinque corporibus regularibus к Пьеро делла Франческа, della Francesca уже включает рисунок октаэдра, описанного вокруг куба, с восемью гранями куба, лежащими на восьми гранях октаэдра. Три октаэдра, описанные таким образом вокруг единого куба, образовали бы соединение трех октаэдров, но делла Франческа не изображает соединение.[5]
Следующим появлением соединения трех октаэдров в математической литературе является работа 1900 г. Макс Брюкнер, в котором упоминается это и включает фотографию его модели.[2][6]
Голландский художник М. К. Эшер, в его гравюре 1948 года Звезды В качестве центральной фигуры гравюры на дереве используется клетка этой формы, содержащая два хамелеоны и парящий в космосе.[7] Эшер не был бы знаком с работами Брюкнера и Х. С. М. Кокстер пишет: «Замечательно, что Эшер, не зная алгебры или аналитической геометрии, смог заново открыть эту в высшей степени симметричную фигуру».[2] Ранее в 1948 году Эшер сделал предварительную гравюру на дереве на похожую тему: Этюд для звезд, но вместо того, чтобы использовать в своем исследовании соединение трех правильных октаэдров, он использовал другую, но родственную форму, звездчатый ромбический додекаэдр (иногда называемое твердым телом Эшера), которое может быть образовано как соединение трех уплощенных октаэдров.[8] Эта форма как многогранник топологически идентична форме Додекаэдр, который можно рассматривать как ромбический додекаэдр с более короткими пирамидами на ромбических гранях. Двойная фигура октаэдрического соединения, соединения трех кубов, также показана на более поздней гравюре Эшера, Водопад, рядом с таким же звездчатым ромбическим додекаэдром.[7]
Соединение трех октаэдров вернулось в математическую литературу более правильно с работами Бакос и Джонсон (1959), который наблюдал за его существованием и предоставил координаты его вершин. Более подробно его изучили Веннингер (1968) и Кокстер (1985).
Другие соединения трех октаэдров
Октаэдры выглядят как треугольные антипризмы, другая форма призматическое соединение антипризм существует с D3D симметрия, порядок 12. Каждая антипризма повернута на 40 градусов. Видно, что верхняя и нижняя плоскости содержат соединение. эннеаграмма, {9/3} или 3 {3}.
Смотрите также
- Соединение четырех октаэдров
- Соединение пяти октаэдров
- Соединение десяти октаэдров
- Соединение двадцати октаэдров
Рекомендации
- ^ а б Бакос, Т .; Джонсон, Норман В. (1959), «Октаэдры, вписанные в куб», Математический вестник, 43 (343): 17–20, JSTOR 3608867.
- ^ а б c d е ж грамм Кокстер, Х. С. М. (1985), "Специальная рецензия на книгу: М. К. Эшер: Его жизнь и полная графическая работа", Математический интеллект, 7 (1): 59–69, Дои:10.1007 / BF03023010. Обсуждение соединения трех октаэдров находится на стр. 61–62.
- ^ Веннингер, М. Дж. (1968), «Некоторые интересные октаэдрические соединения», Математический вестник, 52 (379): 16–23, JSTOR 3614454.
- ^ а б Шепард, Г.С. (1999), "Изоэдральные дельтаэдры", Periodica Mathematica Hungarica, 39 (1–3): 83–106, Дои:10.1023 / А: 1004838806529.
- ^ Харт, Джордж У. (1998), "Многогранники Пьеро делла Франческа", Виртуальные многогранники.
- ^ Брюкнер, Макс (1900), Vielecke und Vielflache, Лейпциг: Teubner, p. 188 и Тафель VIII 12. Как цитирует Кокстер (1985).
- ^ а б Харт, Джордж У. (1996), "Многогранники М. К. Эшера", Виртуальные многогранники.
- ^ Соединение трех октаэдров и замечательного соединения трех квадратных дипирамид, твердого тела Эшера., Ливио Зефиро, Университет Генуи.