Групповое кольцо - Group ring

В алгебра, а групповое кольцо это бесплатный модуль и в то же время звенеть, построенный естественным образом из любого данного кольца и любого данного группа. Как свободный модуль, его кольцо скаляров является данным кольцом, а его базис взаимно однозначен с данной группой. Как кольцо, его закон сложения - это закон свободного модуля, и его умножение расширяет «по линейности» данный групповой закон на основе. Менее формально групповое кольцо представляет собой обобщение данной группы путем присоединения к каждому элементу группы «весового коэффициента» из данного кольца.

Групповое кольцо также называют групповая алгебра, поскольку это действительно алгебра по данному кольцу. Групповая алгебра над полем имеет следующую структуру: Алгебра Хопфа; в этом случае он называется групповая алгебра Хопфа.

Аппарат групповых колец особенно полезен в теории групповые представления.

Определение

Позволять грамм - группа, записанная мультипликативно, и пусть р несущий. Групповое кольцо грамм над р, который мы обозначим через р[грамм] (или просто RG), - множество отображений ж : грамм → р из конечная поддержка,^[1] где модульное скалярное произведение αf скаляра α в р и вектор (или отображение) ж определяется как вектор ${ Displaystyle х mapsto alpha cdot f (x)}$ , а модульная групповая сумма двух векторов ж и грамм определяется как вектор ${ Displaystyle х mapsto f (x) + g (x)}$ . Чтобы включить аддитивную группу р[грамм] в кольцо, определим произведение ж и грамм быть вектором

{ displaystyle x mapsto sum _ {uv = x} f (u) g (v) = sum _ {u in G} f (u) g (u ^ {- 1} x).}

Суммирование правомерно, потому что ж и грамм имеют конечный носитель, и аксиомы кольца легко проверяются.

Используются некоторые вариации обозначений и терминологии. В частности, такие отображения, как ж : грамм → р иногда записываются как так называемые "формальные линейные комбинации элементов грамм, с коэффициентами в р":^[2]

{ Displaystyle сумма _ {г в G} е (г) г,}

или просто

{ displaystyle sum _ {g in G} f_ {g} g,}

где это не вызывает путаницы.^[1]

Примеры

1. Пусть грамм = C₃, то циклическая группа порядка 3, с генератором ${ displaystyle a}$ и элемент идентичности 1_грамм. Элемент р из C[грамм] можно записать как

{ displaystyle r = z_ {0} 1_ {G} + z_ {1} a + z_ {2} a ^ {2} ,}

куда z₀, z₁ и z₂ находятся в C, то сложные числа. Это то же самое, что и кольцо многочленов в переменной ${ displaystyle a}$ такой, что ${ displaystyle a ^ {3} = a ^ {0} = 1}$ т.е. C[грамм] изоморфно кольцу C[ ${ displaystyle a}$ ]/ ${ displaystyle (а ^ {3} -1)}$ .

Написание другого элемента s в качестве ${ displaystyle s = w_ {0} 1_ {G} + w_ {1} a + w_ {2} a ^ {2}}$ , их сумма

{ Displaystyle г + s = (z_ {0} + w_ {0}) 1_ {G} + (z_ {1} + w_ {1}) a + (z_ {2} + w_ {2}) a ^ {2 } ,}

и их продукт

{ displaystyle rs = (z_ {0} w_ {0} + z_ {1} w_ {2} + z_ {2} w_ {1}) 1_ {G} + (z_ {0} w_ {1} + z_ { 1} w_ {0} + z_ {2} w_ {2}) a + (z_ {0} w_ {2} + z_ {2} w_ {0} + z_ {1} w_ {1}) a ^ {2} .}

Обратите внимание, что элемент идентичности 1_грамм из грамм индуцирует каноническое вложение кольца коэффициентов (в данном случае C) в C[грамм]; однако, строго говоря, мультипликативный элемент идентичности C[грамм] составляет 1⋅1_грамм где первый 1 происходит от C а второй из грамм. Аддитивный элемент идентичности равен нулю.

Когда грамм - некоммутативная группа, при умножении членов необходимо соблюдать осторожность, чтобы сохранить порядок элементов группы (и не случайно их коммутировать).

2. Другой пример - Полиномы Лорана над кольцом р: это не что иное, как групповое кольцо бесконечная циклическая группа Z над р.

3. Пусть Q быть группа кватернионов с элементами ${ displaystyle {e, { bar {e}}, i, { bar {i}}, j, { bar {j}}, k, { bar {k}} }}$ . Рассмотрим групповое кольцо рQ, куда р это набор действительных чисел. Произвольный элемент этого группового кольца имеет вид

{ displaystyle x_ {1} cdot e + x_ {2} cdot { bar {e}} + x_ {3} cdot i + x_ {4} cdot { bar {i}} + x_ {5 } cdot j + x_ {6} cdot { bar {j}} + x_ {7} cdot k + x_ {8} cdot { bar {k}}}

куда ${ displaystyle x_ {i}}$ это действительное число.

Умножение, как и в любом другом групповом кольце, определяется на основе групповой операции. Например,

{ Displaystyle { begin {align} { big (} 3 cdot e + { sqrt {2}} cdot i { big)} { big (} { frac {1} {2}} cdot { bar {j}} { big)} & = (3 cdot e) ({ frac {1} {2}} cdot { bar {j}}) + ({ sqrt {2}} cdot i) ({ frac {1} {2}} cdot { bar {j}}) & = { frac {3} {2}} cdot { big (} (e) ( { bar {j}}) { big)} + { frac { sqrt {2}} {2}} cdot { big (} (i) ({ bar {j}}) { big )} & = { frac {3} {2}} cdot { bar {j}} + { frac { sqrt {2}} {2}} cdot k end {align}}. }

Обратите внимание, что рQ не то же самое, что Гамильтон кватернионы над р. Это связано с тем, что кватернионы Гамильтона удовлетворяют дополнительным соотношениям в кольце, таким как ${ Displaystyle -1 cdot я = -i}$ , а в групповом кольце рQ, ${ displaystyle -1 cdot i}$ не равно ${ displaystyle 1 cdot { bar {i}}}$ . Чтобы быть более конкретным, рQ имеет размер 8 как реальный векторное пространство, а кватернионы Гамильтона имеют размерность 4 как реальное векторное пространство.

Некоторые основные свойства

Использование 1 для обозначения мультипликативного тождества кольца р, и обозначив единицу группы 1_грамм, кольцо р[грамм] содержит подкольцо, изоморфное р, а его группа обратимых элементов содержит подгруппу, изоморфную грамм. Для рассмотрения индикаторная функция из {1_грамм}, который является вектором ж определяется

{ displaystyle f (g) = 1 cdot 1_ {G} + sum _ {g not = 1_ {G}} 0 cdot g = mathbf {1} _ { {1_ {G} }} (g) = { begin {cases} 1 & g = 1_ {G} 0 & g neq 1_ {G} end {cases}},}

множество всех скалярных кратных ж это подкольцо р[грамм] изоморфен р. И если мы сопоставим каждый элемент s из грамм к индикаторной функции {s}, который является вектором ж определяется

{ displaystyle f (g) = 1 cdot s + sum _ {g not = s} 0 cdot g = mathbf {1} _ { {s }} (g) = { begin {cases} 1 & g = s 0 & g neq s end {case}}}

получившееся отображение является гомоморфизмом инъективных групп (относительно умножения, а не сложения в р[грамм]).

Если р и грамм оба коммутативны (т. е. р коммутативен и грамм является абелева группа ), р[грамм] коммутативен.

Если ЧАС это подгруппа из грамм, тогда р[ЧАС] это подкольцо из р[грамм]. Аналогично, если S это подкольцо р, S[грамм] является подкольцом р[грамм].

{ displaystyle (1-g) (1 + g + ... + g ^ {m-1}) = 1-g ^ {m} = 1-1 = 0}

Например, рассмотрим групповое кольцо Z[S₃] и элемент порядка 3 грамм= (123). В этом случае,

{ Displaystyle (1- (123)) (1+ (123) + (132)) = 1- (123) ^ {3} = 1-1 = 0}

Групповая алгебра над конечной группой

Групповые алгебры естественным образом возникают в теории групповые представления из конечные группы. Групповая алгебра K[грамм] над полем K по сути является групповым кольцом с полем K заняв место кольца. Как набор и векторное пространство, это свободное векторное пространство на грамм над полем K. То есть для Икс в K[грамм],

{ displaystyle x = sum _ {g in G} a_ {g} g.}

В алгебра структура в векторном пространстве определяется с помощью умножения в группе:

{ displaystyle g cdot h = gh,}

где слева, грамм и час указывают элементы групповой алгебры, а умножение справа - это групповая операция (обозначается сопоставлением).

Поскольку приведенное выше умножение может сбивать с толку, можно также написать базисные векторы из K[грамм] в качестве е_грамм (вместо грамм), и в этом случае умножение записывается как:

{ displaystyle e_ {g} cdot e_ {h} = e_ {gh}.}

Интерпретация как функции

Думая о свободное векторное пространство в качестве K-значные функции на граммумножение алгебры свертка функций.

В то время как групповая алгебра конечный группу можно отождествить с пространством функций на группе, для бесконечной группы они разные. Групповая алгебра, состоящая из конечный сумм, соответствует функциям на группе, которые обращаются в нуль при окончательно много очков; топологически (используя дискретная топология ), они соответствуют функциям с компактная опора.

Однако групповая алгебра K[грамм] и пространство функций K^грамм : = Hom (грамм, K) двойственны: задан элемент групповой алгебры

{ Displaystyle х = сумма _ {г в G} а_ {г} г}

и функция на группе ж : грамм → K эти пары, чтобы дать элемент K через

{ Displaystyle (х, е) = сумма _ {г в G} а_ {г} е (г),}

что является вполне определенной суммой, поскольку она конечна.

Регулярное представительство

Групповая алгебра - это алгебра над собой; при соответствии представлений по р и р[грамм] модулей, это регулярное представительство группы.

Написанное как представление, это представление грамм ↦ ρ_грамм с действием, данным ${ displaystyle rho (g) cdot e_ {h} = e_ {gh}}$ , или же

{ Displaystyle rho (g) cdot r = sum _ {h in G} k_ {h} rho (g) cdot e_ {h} = sum _ {h in G} k_ {h} e_ {gh}.}

Характеристики

Размерность векторного пространства K[грамм] просто равно количеству элементов в группе. Поле K обычно считается комплексными числами C или реальные р, так что можно говорить о групповых алгебрах C[грамм] или же р[грамм].

Групповая алгебра C[грамм] конечной группы над комплексными числами является полупростое кольцо. Этот результат, Теорема Машке, позволяет нам понять C[грамм] как конечный товар из матричные кольца с записями в C.

Представления групповой алгебры

Принимая K[грамм], чтобы быть абстрактной алгеброй, можно попросить конкретную представления алгебры над векторным пространством V. Такое представление

{ displaystyle { tilde { rho}}: K [G] rightarrow { mbox {End}} (V).}

является гомоморфизмом алгебры из групповой алгебры в множество эндоморфизмы на V. Принимая V быть абелева группа, с групповым сложением, задаваемым векторным сложением, такое представление фактически является оставили K[грамм] -модуль над абелевой группой V. Это демонстрируется ниже, где подтверждается каждая аксиома модуля.

Выбирать р ∈ K[грамм] так что

{ displaystyle { tilde { rho}} (r) in { mbox {End}} (V).}

потом ${ Displaystyle { тильда { rho}} (г)}$ является гомоморфизмом абелевых групп в том смысле, что

{ displaystyle { tilde { rho}} (r) cdot (v_ {1} + v_ {2}) = { tilde { rho}} (r) cdot v_ {1} + { tilde { rho}} (r) cdot v_ {2}}

для любого v₁, v₂ ∈ V. Далее следует отметить, что множество эндоморфизмов абелевой группы является кольцо эндоморфизмов. Представление ${ Displaystyle { тильда { rho}}}$ является гомоморфизмом колец, в котором

{ displaystyle { tilde { rho}} (r + s) cdot v = { tilde { rho}} (r) cdot v + { tilde { rho}} (s) cdot v}

для любых двоих р, s ∈ K[грамм] и v ∈ V. Точно так же при умножении

{ displaystyle { tilde { rho}} (rs) cdot v = { tilde { rho}} (r) cdot { tilde { rho}} (s) cdot v.}

Наконец, есть, что единица отображается на личность:

{ Displaystyle { тильда { rho}} (1) cdot v = v}

где 1 - мультипликативная единица K[грамм]; то есть,

{ displaystyle 1 = e_ {e}}

- вектор, соответствующий единице е в грамм.

Последние три уравнения показывают, что ${ Displaystyle { тильда { rho}}}$ является гомоморфизмом колец из K[грамм], взятой как групповое кольцо, в кольцо эндоморфизмов. Первое тождество показало, что отдельные элементы являются гомоморфизмами групп. Таким образом, представление ${ Displaystyle { тильда { rho}}}$ левый K[грамм] -модуль над абелевой группой V.

Обратите внимание, что с учетом общего K[грамм] -модулем индуцируется структура векторного пространства на V, в котором есть дополнительная аксиома

{ displaystyle { tilde { rho}} (ar) cdot v_ {1} + { tilde { rho}} (br) cdot v_ {2} = a { tilde { rho}} (r ) cdot v_ {1} + b { tilde { rho}} (r) cdot v_ {2} = { tilde { rho}} (r) cdot (av_ {1} + bv_ {2} )}

для скаляра а, б ∈ K.

Любое групповое представительство

{ Displaystyle rho: G rightarrow { mbox {Aut}} (V),}

с V векторное пространство над полем K, может быть расширен до представления алгебры

{ Displaystyle { тильда { rho}}: K [G] rightarrow { mbox {End}} (V),}

просто позволив ${ Displaystyle { тильда { rho}} (e_ {g}) = rho (g)}$ и простираясь линейно. Таким образом, представления группы точно соответствуют представлениям алгебры, и поэтому в определенном смысле говорить об одном - это то же самое, что говорить о другом.

Центр групповой алгебры

В центр групповой алгебры - это набор элементов, коммутирующих со всеми элементами групповой алгебры:

{ Displaystyle mathrm {Z} (К [G]): = left {z in K [G]: forall r in K [G], zr = rz right }.}

Центр равен множеству функции класса, то есть набор элементов, постоянных на каждом классе сопряженности

{ Displaystyle mathrm {Z} (К [G]) = left { sum _ {g in G} a_ {g} g: forall g, h in G, a_ {g} = a_ { h ^ {- 1} gh} right }.}

Если K = C, множество неприводимых символы из грамм образует ортонормированный базис Z (K[грамм]) относительно внутреннего продукта

{ displaystyle left langle sum _ {g in G} a_ {g} g, sum _ {g in G} b_ {g} g right rangle = { frac {1} {| G |}} sum _ {g in G} { bar {a}} _ {g} b_ {g}.}

Групповые кольца над бесконечной группой

Гораздо меньше известно о случае, когда грамм исчисляемо бесконечно или несчетно, и это область активных исследований.^[3] Случай, когда р - это, вероятно, наиболее изученная область комплексных чисел. В этом случае, Ирвинг Каплански доказал, что если а и б являются элементами C[грамм] с ab = 1, тогда ба = 1. Верно ли это, если р - поле положительной характеристики, остается неизвестным.

Давняя гипотеза Капланского (~ 1940) гласит, что если грамм это группа без кручения, и K поле, то групповое кольцо K[грамм] не имеет нетривиальных делители нуля. Эта гипотеза эквивалентна K[грамм], не имеющий нетривиальных нильпотенты при тех же гипотезах для K и грамм.

Фактически условие, что K поле можно ослабить до любого кольца, которое можно вложить в область целостности.

Гипотеза остается открытой в полной общности, однако было показано, что некоторые частные случаи групп без кручения удовлетворяют гипотезе о делителе нуля. К ним относятся:

Уникальные группы товаров (например, заказываемые группы, особенно бесплатные группы )
Элементарные поддающиеся группе (например. практически абелевы группы )
Диффузные группы - в частности, группы, свободно действующие изометрически на р-деревья и фундаментальные группы групп поверхностей, за исключением фундаментальных групп прямых сумм одного, двух или трех экземпляров проективной плоскости.

Случай грамм быть топологическая группа более подробно обсуждается в статье групповая алгебра локально компактной группы.

Представления группового кольца

Модуль M над р[грамм] тогда то же самое, что и линейное представление из грамм над полем р. Нет особых причин ограничивать р быть здесь полем. Однако классические результаты были получены впервые, когда р это комплексное число поле и грамм конечная группа, поэтому этот случай заслуживает пристального внимания. Было показано, что р[грамм] это полупростое кольцо, в этих условиях, с глубокими последствиями для представлений конечных групп. В более общем смысле, когда характеристика поля р не делит порядок конечной группы грамм, тогда р[грамм] полупростой (Теорема Машке ).

Когда грамм конечный абелева группа, групповое кольцо коммутативно, и его структуру легко выразить через корни единства. Когда р поле характеристики п, а простое число п делит порядок конечной группы грамм, то групповое кольцо нет полупростой: имеет ненулевое Радикал Якобсона, и это дает соответствующий предмет модульная теория представлений свой собственный, более глубокий характер.

Теория категорий

Примыкающий

Категорически, конструкция группового кольца левый смежный к "группа единиц "; следующие функторы являются сопряженная пара:

{ displaystyle R [-] двоеточие mathbf {Grp} to R mathbf {{ text {-}} Alg}}

{ displaystyle (-) ^ { times} двоеточие R mathbf {{ text {-}} Alg} to mathbf {Grp}}

куда ${ Displaystyle R [-]}$ переводит группу в ее групповое кольцо над р, и ${ Displaystyle (-) ^ { раз}}$ занимает р-алгебра к своей группе единиц.

Когда р = Z, это дает примыкание между категория групп и категория колец, а единица присоединения занимает группу грамм в группу, содержащую тривиальные единицы: грамм × {±1} = {±грамм}. В общем случае групповые кольца содержат нетривиальные единицы. Если грамм содержит элементы а и б такой, что ${ Displaystyle а ^ {п} = 1}$ и б не нормализует ${ displaystyle langle a rangle}$ затем квадрат

{ Displaystyle х = (а-1) б влево (1 + а + а ^ {2} + ... + а ^ {п-1} вправо)}

равен нулю, поэтому ${ Displaystyle (1 + х) (1-х) = 1}$ . Элемент 1 + Икс - единица бесконечного порядка.

Универсальная собственность

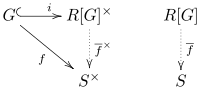
Приведенное выше присоединение выражает универсальное свойство групповых колец.^[1]^[4] Позволять р - (коммутативное) кольцо, пусть грамм быть группой, и пусть S быть р-алгебра. Для любого гомоморфизма групп ${ displaystyle f: G to S ^ { times}}$ , существует единственный р-алгебр гомоморфизм ${ displaystyle { overline {f}}: R [G] to S}$ такой, что ${ displaystyle { overline {f}} circ i = f}$ куда я это включение

{ displaystyle { begin {выравнивается} i: G & longrightarrow R [G] g & longmapsto 1_ {R} g end {выравнивается}}}

Другими словами, ${ displaystyle { overline {f}}}$ - единственный гомоморфизм, коммутирующий следующую диаграмму:

Любое другое кольцо, удовлетворяющее этому свойству, является канонически изоморфна групповому кольцу.

Обобщения

Групповая алгебра обобщается на моноидное кольцо и оттуда в алгебра категорий, из которых другим примером является алгебра инцидентности.

Фильтрация

Если в группе есть функция длины - например, если есть выбор генераторов и берется слово метрика, как в Группы Кокстера - тогда групповое кольцо становится фильтрованная алгебра.

Смотрите также

Теория представлений

Теория категорий

Примечания

^ ^а ^б ^c Polcino & Sehgal (2002), стр. 131.
^ Polcino & Sehgal (2002), стр. 129 и 131.
^ Пассман, Дональд С. (1976). "Что такое групповое кольцо?". Амер. Математика. Ежемесячно. 83: 173–185. Дои:10.2307/2977018.
^ "групповая алгебра в nLab". ncatlab.org. Получено 2017-11-01.

Групповое кольцо - Group ring

Содержание

Определение

Примеры

Некоторые основные свойства

Групповая алгебра над конечной группой

Интерпретация как функции

Регулярное представительство

Характеристики

Представления групповой алгебры

Центр групповой алгебры

Групповые кольца над бесконечной группой

Представления группового кольца

Теория категорий

Примыкающий

Универсальная собственность

Обобщения

Фильтрация

Смотрите также

Теория представлений

Теория категорий

Примечания

Рекомендации