Рассечение на ортосхемы - Dissection into orthoschemes - Wikipedia

Нерешенная проблема в математике: Можно ли разрезать каждый симплекс на ограниченное число орто-схем? (больше нерешенных задач по математике)

В геометрии это нерешенный догадка из Хьюго Хадвигер что каждый симплекс возможно рассеченный в орто-схемы, используя ряд ортосхем, ограниченных функцией размерности симплекса.^[1] Если это правда, то в целом каждый выпуклый многогранник могут быть разделены на орто-схемы.

Определения и заявление

В этом контексте симплекс в ${ displaystyle d}$-размерный Евклидово пространство это выпуклый корпус из ${ displaystyle d + 1}$ моменты, которые не все лежат в общих гиперплоскость. Например, двумерный симплекс - это просто треугольник (выпуклая оболочка из трех точек на плоскости), а трехмерный симплекс - это тетраэдр (выпуклость четырех точек в трехмерном пространстве). Точки, образующие таким образом симплекс, называются его вершины.

Орто-схема, также называемая симплексом путей, представляет собой особый вид симплекса. В нем вершины можно соединить дорожка, так что каждые два ребра на пути расположены под прямым углом друг к другу. Двумерная ортосхема - это прямоугольный треугольник. Трехмерную ортосхему можно построить из куб найдя путь из трех ребер куба, которые не все лежат на одной квадратной грани, и сформировав выпуклую оболочку из четырех точек на этом пути.

Разбиение куба на шесть ортосхем

Рассечение фигуры ${ displaystyle S}$ (который может быть любым закрытый набор в евклидовом пространстве) является представлением ${ displaystyle S}$ как объединение других форм, чьи интерьеры находятся не пересекаются друг с другом. То есть интуитивно понятно, что фигуры в объединении не перекрываются, хотя могут иметь общие точки на своих границах. Например, куб можно разделить на шесть трехмерных орто-схем. Аналогичный результат применим и в более общем смысле: каждый гиперкуб или же гипер прямоугольник в ${ displaystyle d}$ размеры можно разрезать на ${ displaystyle d!}$ орто-схемы.

Гипотеза Хадвигера состоит в том, что существует функция ${ displaystyle f}$ так что каждый ${ displaystyle d}$-мерный симплекс можно разрезать не более чем на ${ displaystyle f (d)}$ орто-схемы. Хадвигер поставил эту проблему в 1956 году;^[2] в целом он остается нерешенным, хотя частные случаи при малых значениях ${ displaystyle d}$ известны.^[1]

В небольших размерах

Высота под острым углом может не разрезать треугольник, но высота под самым широким углом всегда разделяет его на два прямоугольных треугольника.

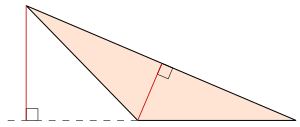
В двух измерениях каждый треугольник можно разрезать не более чем на два прямоугольных треугольника, отбросив высота от самого широкого угла до самого длинного края.^[2]

В трехмерном пространстве некоторые тетраэдры можно разрезать аналогичным образом, сбросив высоту перпендикулярно вершине. ${ displaystyle v}$ в точку ${ displaystyle p}$ в противоположном лице, соединяя ${ displaystyle p}$ перпендикулярно сторонам лица и используя трехреберные перпендикулярные пути через ${ displaystyle v}$ и ${ displaystyle p}$ в сторону, а затем в макушку лица.^[2] Однако это не всегда работает. В частности, существуют тетраэдры, у которых ни одна из вершин не имеет высоты с основанием внутри противоположной грани. С помощью более сложной конструкции Ленхард (1960) Доказано, что каждый тетраэдр можно разрезать не более чем на 12 орто-схем.^[3]Бём (1980) доказал, что это оптимально: существуют тетраэдры, которые нельзя разрезать менее чем на 12 ортосхем.^[4] В той же статье Бем также обобщил результат Ленхарда на трехмерную сферическая геометрия и трехмерный гиперболическая геометрия.

В четырех измерениях требуется не более 500 орто-схем.^[5] В пяти измерениях снова требуется конечное число орто-схем, примерно ограниченное максимум 12,5 миллионами. Опять же, это относится к сферической геометрии и гиперболической геометрии, а также к евклидовой геометрии.^[6]

Гипотеза Хадвигера остается недоказанной для всех измерений больше пяти.^[1]

Последствия

Каждый выпуклый многогранник могут быть разбиты на симплексы. Следовательно, если гипотеза Хадвигера верна, каждый выпуклый многогранник также имел бы разрез на ортосхемы.^[6]

Связанный результат состоит в том, что каждая орто-схема может быть разбита на ${ displaystyle d}$ или же ${ displaystyle d + 1}$ меньшие орто-схемы.^[7][8] Следовательно, для симплексов, которые могут быть разбиты на орто-схемы, их разрезы могут иметь сколь угодно большое количество орто-схем.

Рекомендации