Бруннская ссылка - Brunnian link

Это четырехкомпонентное звено является бруннским звеном.
Шестикомпонентное брунновское звено.

В теория узлов, филиал топология, а Бруннская ссылка нетривиальный ссылка на сайт это становится набором тривиальных несвязанный кружки, если удален какой-либо компонент. Другими словами, разрезание любой петли освобождает все остальные петли (так что никакие две петли не могут быть напрямую связаны ).

Название Бруннский после Герман Брунн. Статья Брунна 1892 года Über Verkettung включены примеры таких ссылок.

Примеры

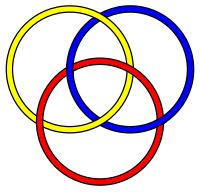
В Кольца Борромео - простейшее бруннское звено.

Самая известная и простая из возможных бруннских ссылок - это Кольца Борромео, ссылка из трех развязки. Однако для каждого числа три или выше существует бесконечное количество связей с брунновским свойством, содержащих такое количество петель. Вот несколько относительно простых трехкомпонентных брунновских связей, которые не совпадают с кольцами Борромео:

  • 12-переходное звено.

  • 18-переходное звено.

  • 24-х переходное звено.

Самым простым бруннским звеном, кроме 6-пересекающихся колец Борромео, по-видимому, является 10-пересекающееся L10a140 ссылка.[1]

Пример п-компонентная Брунновская ссылка дается "Резинка" Брунниан Линкс, где каждый компонент зацикливается на следующем как аба−1б−1, причем последний оборачивается вокруг первого, образуя круг.

Классификация

Бруннские ссылки были классифицированы до связь-гомотопия к Джон Милнор в (Милнор 1954 ), а введенные им инварианты теперь называются Инварианты Милнора.

An (п + 1) -компонентную брунновскую связь можно рассматривать как элемент группа ссылок - что в данном случае (но не в целом) является фундаментальная группа из дополнение ссылки - из п-компонентное отключение, так как по Brunnianness удаление последней ссылки разъединяет остальные. Связующая группа п-компонент unlink - это свободная группа на п генераторы, Fп, поскольку группа ссылок одной ссылки является группа узлов из развязанный, который является целым числом, а связующая группа несвязанного объединения - это бесплатный продукт групп звеньев компонентов.

Не каждый элемент группы ссылок дает брунновскую ссылку, так как удаление любого Другой компонент также должен отсоединить оставшиеся п элементы. Милнор показал, что элементы группы, которые соответствуют брунновским связям, связаны с градуированная алгебра Ли из нижний центральный ряд свободной группы, которые можно интерпретировать как «отношения» в свободная алгебра Ли.

Продукция Massey

Основная статья: Продукция Massey

Бруннские ссылки можно понять в алгебраическая топология через Продукция Massey: продукт Massey - это п-скрученное произведение, которое определяется, только если все (п - 1) -кратные произведения его членов исчезают. Это соответствует брунновскому свойству всех (п - 1) -компонентные подссылки не связаны, но в целом п-компонентная ссылка связана нетривиально.

Бруннские косы

Смотрите также: Закрытая коса
Стандартная коса - бруннианская: если удалить черную прядь, синяя прядь всегда будет поверх красной, и, таким образом, они не переплетаются друг с другом; также для удаления других прядей.

Бруннианец тесьма коса, которая становится тривиальной после удаления любой из ее ниток. Бруннские косы образуют подгруппа из группа кос. Бруннианские косы на 2-сфера которые не являются брунновскими над 2-диск порождают нетривиальные элементы в гомотопических группах 2-сферы. Например, «стандартная» коса, соответствующая кольцам Борромео, дает начало Расслоение Хопфа S3 → S2, и его итерации (как и в повседневном плетении) также являются брунновскими.

Примеры из реального мира

Много распутывание головоломок и немного механические головоломки являются вариантами Brunnian Links, цель которых - освободить одну часть, только частично связанную с остальными, тем самым демонтируя структуру.

Бруннские цепи также используются для создания носимых и декоративных предметов из резинок с помощью таких устройств, как Радужный ткацкий станок или Wonder Loom.

Рекомендации

  1. ^ Бар-Натан, Дрор (2010-08-16). "Все бруннианцы, может быть ", [Академический Омут].

дальнейшее чтение

  • Беррик, А. Джон; Коэн, Фредерик Р .; Вонг, Ян Лой; Ву, Цзе (2006), «Конфигурации, косы и гомотопические группы», Журнал Американского математического общества, 19 (2): 265–326, Дои:10.1090 / S0894-0347-05-00507-2, Г-Н  2188127.
  • Герман Брунн, "Über Verkettung", J. Münch. Бер, XXII. 77–99 (1892). JFM  24.0507.01 (на немецком)
  • Милнор, Джон (Март 1954 г.), "Группы связи", Анналы математики, Анналы математики, 59 (2): 177–195, Дои:10.2307/1969685, JSTOR  1969685
  • Рольфсен, Дейл (1976), Узлы и ссылки, Серия лекций по математике, 7, Беркли, Калифорния: Опубликовать или погибнуть, ISBN  0-914098-16-0, Г-Н  0515288

внешняя ссылка