Аксиомы Тарского - Tarskis axioms - Wikipedia
Аксиомы Тарского, из-за Альфред Тарский, являются аксиома набор для содержательного фрагмента Евклидова геометрия это формулируется в логика первого порядка с личность, и не требуя теория множеств (Тарский 1959 ) (т.е. та часть евклидовой геометрии, которую можно сформулировать как элементарная теория ). Другие современные аксиомизации евклидовой геометрии: Аксиомы Гильберта и Аксиомы Биркгофа.
Обзор
В начале своей карьеры Тарский преподавал геометрию и исследовал теорию множеств. Его коллега Стивен Гивант (1999) объяснил отправную точку Тарского:
- От Энрикеса Тарский узнал о работе Марио Пиери, итальянский геометр, на которого сильно повлиял Пеано. Тарский предпочел систему Пиери [его Точка и сфера мемуары], где логическая структура и сложность аксиом были более прозрачными.
Затем Гивант говорит, что «с типичной тщательностью» Тарский разработал свою систему:
- Чем отличался подход Тарского к геометрии? Прежде всего, система аксиом была намного проще любой из существовавших до того времени систем аксиом. На самом деле длина всех аксиом Тарского, вместе взятых, не намного больше, чем просто одна из 24 аксиом Пиери. Это была первая система евклидовой геометрии, которая была достаточно простой, чтобы все аксиомы можно было выразить через примитивные представления только, без помощи определенных понятий. Еще важнее то, что впервые было проведено четкое различие между полной геометрией и ее элементарной, то есть ее частью первого порядка.
Как и другие современные аксиоматизации евклидовой геометрии, Тарский использует формальная система состоящий из строк символов, называемых фразы, конструкция которого соблюдает формальные синтаксические правила, и правила доказательства, которые определяют допустимые манипуляции с предложениями. В отличие от некоторых других современных аксиоматизаций, таких как Биркгофа и Гильберта Аксиоматизация Тарского не имеет примитивные объекты Кроме как точки, поэтому переменная или константа не может относиться к линии или углу. Поскольку точки - единственные примитивные объекты, а система Тарского - это теория первого порядка, невозможно даже определить линии как наборы точек. Единственные примитивные отношения (предикаты ) являются «промежуточностью» и «совпадением» между точками.
Аксиоматизация Тарского короче, чем ее соперники, в том смысле, в котором Тарский и Гивант (1999) явно указывают на это. Он более краток, чем у Пиери, потому что у Пиери было только два примитивных понятия, в то время как Тарский ввел три: точка, промежуточность и согласованность. Такая экономия примитивных и определенных понятий означает, что система Тарского не очень удобна для делает Евклидова геометрия. Скорее, Тарский разработал свою систему, чтобы облегчить ее анализ с помощью инструментов математическая логика, т.е. чтобы облегчить вывод его метаматематических свойств. Система Тарского обладает необычным свойством: все предложения могут быть записаны в универсально-экзистенциальной форме - частном случае пренекс нормальная форма. В этой форме есть все универсальные кванторы предшествующий любому экзистенциальные кванторы, так что все предложения могут быть преобразованы в форму Этот факт позволил Тарскому доказать, что евклидова геометрия разрешимый: существует алгоритм который может определить истинность или ложность любого предложения. Аксиоматизация Тарского также полный. Это не противоречит Первая теорема Гёделя о неполноте, потому что теории Тарского не хватает выразительной силы, необходимой для интерпретации Арифметика Робинсона (Франзен 2005 С. 25–26).
Аксиомы
Альфред Тарский работал над аксиоматизацией и метаматематикой Евклидова геометрия с перерывами с 1926 года до его смерти в 1983 году, когда Тарский (1959) возвещал о его зрелом интересе к этой теме. Работа Тарского и его учеников по евклидовой геометрии достигла высшей точки в монографии Schwabhäuser, Szmielew, and Tarski (1983), в которой изложены 10 аксиомы и один схема аксиомы показано ниже, связанные метаматематика, и немного по теме. Гупта (1965) внес важный вклад, а Тарски и Гивант (1999) обсуждают историю.
Фундаментальные отношения
Эти аксиомы представляют собой более элегантную версию набора, разработанного Тарским в 1920-х годах в рамках своего исследования метаматематических свойств Евклидова плоская геометрия. Эта цель потребовала переформулировать эту геометрию как теория первого порядка. Тарский сделал это, предположив вселенная из точки, со строчными буквами, обозначающими переменные в пределах этой вселенной. Равенство обеспечивается базовой логикой (см. Логика первого порядка # Равенство и его аксиомы ).[1] Затем Тарский постулировал два примитивных отношения:
- Близость, а тройственное отношение. В атомарное предложение Bxyz означает, что у между" Икс и zдругими словами, что у это точка на отрезок xz. (Это отношение интерпретируется включительно, так что Bxyz тривиально верно всякий раз, когда х = у или же у = г).
- Конгруэнтность (или "равноудаленность"), тетрадное отношение. В атомарное предложение wx ≡ yz можно интерпретировать как wx является конгруэнтный к yzдругими словами, что длина линейного сегмента wx равна длине отрезка yz.
Промежуточность отражает аффинный аспект евклидовой геометрии; конгруэнтность, это метрика аспект. Фоновая логика включает личность, а бинарное отношение. Аксиомы вызывают идентичность (или ее отрицание) пять раз.
Приведенные ниже аксиомы сгруппированы по типам вызываемых ими отношений, затем отсортированы сначала по количеству экзистенциальных кванторов, а затем по количеству элементарных предложений. Аксиомы следует читать как универсальные крышки; следовательно, любой свободные переменные следует воспринимать как молчаливое универсально определяемый.
Аксиомы конгруэнтности
- Рефлексивность конгруэнтности
- Идентичность конгруэнтности
- Транзитивность конгруэнтности
Комментарий
Хотя отношение конгруэнтности формально является четырехсторонним отношением между точками, его также можно неформально рассматривать как бинарное отношение между двумя отрезками линии. и . Приведенные выше аксиомы «Рефлексивности» и «Транзитивности», вместе взятые, доказывают:
- что это бинарное отношение на самом деле отношение эквивалентности
- рефлексивно: .
- это симметрично .
- это переходный .
- и что порядок, в котором указаны точки отрезка, не имеет значения.
- .
- .
- .
Аксиома «транзитивности» утверждает, что конгруэнтность Евклидово, в том, что он уважает первую из Евклида "общие понятия ".
Аксиома «тождества конгруэнтности» интуитивно утверждает, что если ху конгруэнтно отрезку, который начинается и заканчивается в той же точке, Икс и у то же самое. Это тесно связано с понятием рефлексивность за бинарные отношения.
Аксиомы промежуточности

- Идентичность посредничества
Единственная точка на отрезке линии является сам.

- Схема аксиомы преемственности
Пусть φ (Икс) и ψ (у) быть формулы первого порядка не содержащий бесплатные экземпляры либо а или же б. Пусть и бесплатных экземпляров не будет Икс в ψ (у) или у в φ (Икс). Тогда все экземпляры следующей схемы являются аксиомами:
Позволять р быть лучом с конечной точкой а. Пусть формулы первого порядка φ и ψ определяют подмножества Икс и Y из р, так что каждая точка в Y находится справа от каждой точки Икс (относительно а). Тогда существует точка б в р лежащий между Икс и Y. По сути, это Дедекинда вырезать конструкция, проводимая таким образом, чтобы избежать количественной оценки по множествам.
- Ниже Измерение
Существуют три неколлинеарные точки. Без этой аксиомы теория могла бы быть смоделированный одномерным реальная линия, единственная точка или даже пустой набор.
Конгруэнтность и промежуточность

- Верхний Измерение
Три точки, равноудаленные от двух разных точек, образуют линию. Без этой аксиомы теория могла бы быть смоделирована трехмерный или многомерное пространство.
- Аксиома Евклида
Каждый из трех вариантов этой аксиомы, эквивалентных по остальным аксиомам Тарского аксиомам Евклида. параллельный постулат, имеет преимущество перед остальными:
- А обходится без экзистенциальные кванторы;
- B имеет наименьшее количество переменных и атомарные предложения;
- C требует только одного примитивного понятия - промежуточности. Этот вариант обычно приводится в литературе.
- А:
Пусть отрезок прямой соединяется с серединой двух сторон данного треугольник. Этот отрезок линии будет вдвое короче третьей стороны. Это эквивалентно внутренние углы любого треугольника в сумме до двух прямые углы.
- B:
Учитывая любые треугольник, существует круг это включает в себя все его вершины.
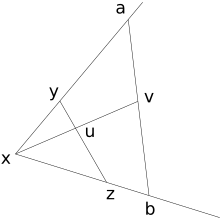
- C:
Учитывая любые угол и любой момент v внутри есть отрезок линии, включающий v, с конечными точками на каждой стороне угла.
- Пять сегментов

Начни с двух треугольники, xuz и x'u'z '. Нарисуйте отрезки линии ю и y'u ', соединение вершины каждого треугольника с точкой на стороне, противоположной вершине. В результате получаются два разделенных треугольника, каждый из которых состоит из пяти сегментов. Если четыре сегмента одного треугольника каждый конгруэнтный сегменту в другом треугольнике, то пятые сегменты в обоих треугольниках должны совпадать.
Это эквивалентно сторона угол сторона правило определения конгруэнтности двух треугольников; если углы uxz и u'x'z ' конгруэнтны (существуют конгруэнтные треугольники xuz и x'u'z '), и две пары инцидентных сторон конгруэнтны (xu ≡ x'u ' и xz ≡ x'z '), то оставшаяся пара сторон также конгруэнтна (uz ≡ u'z ').
- Строительство сегмента
Для любой точки у, можно рисовать в любом направлении (определяется Икс) прямая, конгруэнтная любому отрезку ab.
Обсуждение
Начиная с двух примитивных связи чьи поля являются плотный вселенная из точки, Тарский построил геометрию отрезки линии. Согласно Тарски и Гиванту (1999: 192-93), ни одно из вышеперечисленных аксиомы принципиально новые. Первые четыре аксиомы устанавливают некоторые элементарные свойства двух примитивных отношений. Например, рефлексивность и транзитивность конгруэнтности устанавливают, что конгруэнтность отношение эквивалентности над линейными сегментами. Тождество конгруэнтности и промежуточности управляет тривиальным случаем, когда эти отношения применяются к нечетким точкам. Теорема ху≡zz ↔ Икс=у ↔ Bxyx расширяет эти аксиомы идентичности.
Ряд других свойств Междунородности можно вывести в виде теорем, в том числе:
- Рефлексивность: Bxxy ;
- Симметрия: Bxyz → Bzyx ;
- Транзитивность: (Bxyw ∧ Byzw) → Bxyz ;
- Связь: (Bxyw ∧ Bxzw) → (Bxyz ∨ Bxzy).
Последние два свойства полностью заказать точки, составляющие отрезок прямой.
Вместе верхнее и нижнее измерения требуют, чтобы любая модель этих аксиом имела определенный конечный размерность. Соответствующие изменения в этих аксиомах дают наборы аксиом для Евклидова геометрия за размеры 0, 1 и больше 2 (Tarski and Givant 1999: Axioms 8(1), 8(п), 9(0), 9(1), 9(п) ). Обратите внимание, что сплошная геометрия не требует новых аксиом, в отличие от случая с Аксиомы Гильберта. Более того, нижняя размерность для п размеры - это просто отрицание верхнего измерения для п - 1 размер.
Когда количество измерений больше 1, промежуточность может быть определена в терминах соответствие (Тарский и Гивант, 1999). Сначала определите отношение «≤» (где интерпретируется "длина отрезка линии меньше или равен длине отрезка линии "):
В случае двух измерений интуиция следующая: для любого отрезка линии хурассмотрим возможный диапазон длин xv, куда v любая точка на серединном перпендикуляре к ху. Очевидно, что пока нет верхней границы длины xv, существует нижняя граница, которая возникает при v это середина ху. Так что если ху короче или равно цзу, то диапазон возможных длин xv будет надмножеством диапазона возможных длин zw, куда ш любая точка на серединном перпендикуляре к цзу.
Тогда промежуточность можно определить, используя интуицию, что кратчайшее расстояние между любыми двумя точками - это прямая линия:
Схема аксиом непрерывности гарантирует, что порядок точек на прямой полный (относительно определяемых свойств первого порядка). Аксиомы Pasch и Евклид хорошо известны. Примечательно, что евклидова геометрия требует только следующих дополнительных аксиом:
- Строительство сегмента. Эта аксиома делает измерение и Декартова система координат возможно - просто присвоить значение 1 некоторому произвольному непустому отрезку линии;[требуется разъяснение ]
Позволять wff стоять за правильно сформированная формула (или синтаксически правильная формула) элементарной геометрии. Тарский и Гивант (1999: 175) доказали, что элементарная геометрия:
- Последовательный: Не существует такого wff, что и оно, и его отрицание являются теоремами;
- Полный: Каждое предложение или его отрицание - это теорема, доказываемая на основе аксиом;
- Разрешимый: Существует алгоритм который присваивает значение истины к каждому предложению. Это следует из Тарского:
- Порядок принятия решения для настоящее закрытое поле, который он нашел исключение квантора (в Теорема Тарского – Зайденберга. );
- Аксиомы, допускающие (многомерное) верное интерпретация как настоящее закрытое поле.
Гупта (1965) доказал независимость указанных выше аксиом, Pasch и Рефлексивность конгруэнтности за исключением.
Отрицание аксиомы Евклида дает гиперболическая геометрия, исключая его, дает абсолютная геометрия. Полная (в отличие от элементарной) евклидова геометрия требует отказа от аксиоматизации первого порядка: заменить φ (Икс) и ψ (у) в схеме аксиом непрерывности с Икс ∈ А и у ∈ B, куда А и B универсальные количественные переменные, варьирующиеся по множеству точек.
Сравнение с Гильбертом
Аксиомы Гильберта для плоской геометрии номер 16, и включают транзитивность сравнения и вариант аксиомы Паша. Единственное понятие интуитивной геометрии, используемое в комментариях к аксиомам Тарского, - это треугольник. (Версии B и C аксиомы Евклида относятся к «кругу» и «углу» соответственно.) Аксиомы Гильберта также требуют «луча», «угла» и понятия треугольника, «включающего в себя» угол. В дополнение к промежуточности и конгруэнтности аксиомы Гильберта требуют примитивного бинарное отношение "on", связывая точку и линию. В Схема аксиомы непрерывности играет роль, аналогичную двум аксиомам непрерывности Гильберта. Эта схема незаменима; Евклидова геометрия на языке Тарского (или аналогичного) не может быть аксиоматизирована с конечной аксиоматизацией как теория первого порядка. Аксиомы Гильберта не составляют теорию первого порядка, потому что его аксиомы непрерывности требуют логика второго порядка.
Первые четыре группы аксиом Аксиомы Гильберта поскольку плоская геометрия интерпретируема с аксиомами Тарского минус непрерывность.
Смотрите также
Примечания
- ^ Тарский и Гивант, 1999, стр.177.
Рекомендации
- Франзен, Торкель (2005), Теорема Гёделя: неполное руководство по ее использованию и злоупотреблениям, А. К. Питерс, ISBN 1-56881-238-8
- Гивант, Стивен (1999) «Объединяющие нити в работе Альфреда Тарски», Математический интеллигент 21:47–58.
- Гупта, Х. Н. (1965) Вклад в аксиоматические основы геометрии. Кандидат наук. защитил диссертацию в Калифорнийском университете в Беркли.
- Тарский, Альфред (1959), «Что такое элементарная геометрия?», Леон Хенкин, Патрик Суппес и Альфред Тарски (ред.), Аксиоматический метод. Особое внимание уделяется геометрии и физике. Материалы международного симпозиума в Univ. из Калифорнии, Беркли, 26 декабря 1957 г. - янв. 4 января 1958 г., Исследования по логике и основам математики, Амстердам: Северная Голландия, стр. 16–29, МИСТЕР 0106185. Доступен как 2007 перепечатка, Брауэр Пресс, ISBN 1-4437-2812-8
- Тарский, Альфред; Гивант, Стивен (1999), "Система геометрии Тарского", Вестник символической логики, 5 (2): 175–214, CiteSeerX 10.1.1.27.9012, Дои:10.2307/421089, ISSN 1079-8986, JSTOR 421089, МИСТЕР 1791303
- Швабхойзер, В., Шмелев, В., и Альфред Тарский, 1983. Metamat Mathematische Methoden in der Geometrie. Springer-Verlag.
- Щерба, Л. В. (1986). «Тарский и геометрия». Журнал символической логики. 51 (4): 907–12. Дои:10.2307/2273904. JSTOR 2273904.


















![{ Displaystyle существует a , forall x , forall y , [( phi (x) land psi (y)) rightarrow Baxy] rightarrow существует b , forall x , forall y , [( phi (x) land psi (y)) rightarrow Bxby].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59ae3e756b25e36737ce1b1a821a1eccb189f93c)
![{ Displaystyle существует а , существует b , существует с , [ neg Babc land neg Bbca land neg Bcab].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd22fec38e8bcb55b3e60eb02646168494f74830)





![{ Displaystyle существует z , [Bxyz land yz Equiv ab].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af5dc21bc5573743744ec88249eb2043f46cc35a)




