Теорема Штейница - Steinitzs theorem - Wikipedia

Результат об условно сходящихся рядах векторов см. Теорема Леви – Стейница..

В многогранная комбинаторика, раздел математики, Теорема Стейница это характеристика неориентированные графы образованный ребрами и вершинами трехмерных выпуклые многогранники: они точно такие (просто ) 3-вершинно-связанный планарные графы (минимум с четырьмя вершинами). То есть каждый выпуклый многогранник образует 3-связный плоский граф, а каждый 3-связный плоский граф может быть представлен как график выпуклого многогранника. По этой причине трехсвязные планарные графы также известны как многогранные графы.[1] Бранко Грюнбаум назвал эту теорему «наиболее важным и наиболее глубоким из известных результатов о 3-многогранники.”[2]

Теорема появилась в статье 1922 г. Эрнст Стейниц, в честь кого назван. Это может быть доказано математическая индукция (как это сделал Стейниц), найдя состояние с минимальной энергией двухмерной пружинной системы и перенеся результат в три измерения, или используя теорема об упаковке кругов. Известно несколько расширений теоремы, в которых многогранник, реализующий данный граф, имеет дополнительные ограничения; например, каждый многогранный граф является графиком выпуклого многогранника с целыми координатами или графиком выпуклого многогранника, все ребра которого касаются общего средняя сфера.

В более высоких измерениях проблема описания графиков выпуклые многогранники остается открытым.

Определения и формулировка теоремы

Освещение скелета выпуклого многогранника от источника света, расположенного близко к одной из его граней, приводит к тому, что его тени образуют плоскую форму. Диаграмма Шлегеля.

An неориентированный граф это система вершины и края, каждое ребро соединяет две вершины. Из любого многогранника можно составить граф, положив вершины графа на вершины многогранника и соединением любых двух вершин графа ребром, если соответствующие две вершины многогранника являются концами ребра многогранника. Этот график известен как скелет многогранника.

График планарный если его можно нарисовать вершинами как точки в Евклидова плоскость, а его ребра - как кривые, соединяющие эти точки, так что никакие две реберные кривые не пересекаются друг с другом, и такая, что точка, представляющая вершину, лежит на кривой, представляющей ребро, только когда вершина является конечной точкой ребра. К Теорема Фари, достаточно рассматривать только плоские чертежи, на которых кривые, изображающие кромки отрезки линии. График 3-связный если после удаления любых двух его вершин любая другая пара вершин остается соединенной путем. Теорема Штейница утверждает, что оба эти условия являются необходимо и достаточно для характеристики скелетов трехмерных выпуклых многогранников: заданный граф грамм является графиком выпуклого трехмерного многогранника тогда и только тогда, когда грамм плоский и 3-вершинно-связный.[3][2]

История и нейминг

Теорема Стейница названа в честь Эрнст Стейниц, который представил свое первое доказательство для публикации в 1916 году.[4]

Название «теорема Стейница» применялось и к другим результатам Стейница:

Доказательства

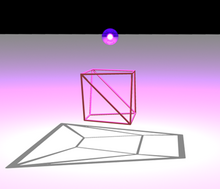
Одно из направлений теоремы Стейница (более легкое для доказательства) гласит, что график любого выпуклого многогранника является плоским и 3-связным. Как показано на рисунке, планарность можно показать с помощью Диаграмма Шлегеля: если поместить источник света рядом с одной гранью многогранника, а плоскость - с другой стороны, тени ребер многогранника образуют плоский граф, вложенный таким образом, что ребра представляют собой отрезки прямых линий. 3-связность многогранного графа - частный случай Теорема Балинского что график любого k-размерный выпуклый многогранник является k-связаны.[11]

Другое, более сложное направление теоремы Стейница утверждает, что каждый планарный 3-связный граф является графиком выпуклого многогранника. Для этой части есть три стандартных подхода: доказательства по индукции, двумерное поднятие. Вложения Тутте в трех измерениях, используя соответствие Максвелла – Кремоны, и методы, использующие теорема об упаковке кругов создать канонический многогранник.

Индукция

Δ-Y и Y-Δ преобразования многогранника

Первоначальное доказательство Стейница заключалось в нахождении последовательности Δ-Y и Y-Δ преобразовывает которые сводят любой трехсвязный планарный граф к K4, график тетраэдра. Преобразование Y-Δ удаляет вершину третьей степени из графа, добавляя ребра между всеми ее бывшими соседями, если эти ребра еще не существовали; обратное преобразование, преобразование Δ-Y, удаляет ребра треугольника из графа и заменяет их новой вершиной третьей степени, смежной с теми же тремя вершинами. Как только такая последовательность найдена, ее можно перевернуть, чтобы получить последовательность преобразований Δ-Y и Y-Δ, которые шаг за шагом создают желаемый многогранник, начиная с многогранника. Каждое преобразование Y-Δ в этой последовательности может быть выполнено путем отсечения вершины третьей степени от многогранника. Преобразование Δ-Y может быть выполнено путем удаления треугольной грани многогранника и расширения его соседних граней до точки, где они встречаются, но только тогда, когда эта тройная точка пересечения трех соседних граней находится на правильной стороне многогранника; когда тройная точка пересечения находится не на правильной стороне, проективное преобразование многогранника достаточно, чтобы сдвинуть его на правильную сторону. Следовательно, индукцией по количеству преобразований Δ-Y и Y-Δ, необходимых для сведения данного графа к K4, любой многогранный граф можно реализовать как многогранник.[4]

Более поздняя работа Епифанова усилила доказательство Стейница, что любой многогранный граф сводится к K4 на Δ-Y и Y-Δ преобразовывает. Епифанов доказал, что если в плоском графе заданы две вершины, то граф можно свести к единственному ребру между этими терминалами, объединив преобразования Δ-Y и Y-Δ с последовательно-параллельные редукции.[12] Доказательство Епифанова было сложным и неконструктивным, но Трумпер упростил его, используя методы, основанные на граф миноры. Трумпер заметил, что каждый сеточный график сводится с помощью преобразований Δ-Y и Y-Δ таким образом, что эта сводимость сохраняется минорами графа и что каждый планарный граф является минором сеточного графа.[13] Эту идею можно использовать для замены леммы Стейница о существовании редукционной последовательности в доказательстве теоремы Стейница с использованием индукции таким же образом.[3] Однако существуют графы, требующие нелинейного количества шагов в любой последовательности преобразований Δ-Y и Y-Δ. Точнее, Ω(п3/2) шаги иногда необходимы, и самый известный верхняя граница по количеству ступенек еще хуже, О(п2).[14]

Альтернативная форма доказательства индукции основана на удалении ребер (и сжатии вершин степени два, которые могут быть выполнены этим удалением) или сжатии ребер и формировании минорной части данного плоского графа. Любой многогранный граф сводится к K4 линейным числом этих операций, и снова операции могут быть обращены, а обратные операции выполнены геометрически, давая многогранную реализацию графа. Однако, хотя проще доказать, что существует редукционная последовательность для этого типа аргумента, а редукционные последовательности короче, геометрические шаги, необходимые для обращения последовательности, более сложны.[15]

Подъем

Равновесное напряжение на графике куба, соответствующее поднятию этого чертежа до трехмерного усеченный

Если график нарисованный в плоскости с прямыми краями, тогда равновесное напряжение определяется как присвоение ненулевых действительных чисел (весов) ребрам с тем свойством, что каждая вершина находится в положении, заданном взвешенной суммой своих соседей. Согласно соответствию Максвелла – Кремоны, равновесное напряжение может быть поднято до кусочно-линейной непрерывной трехмерной поверхности, так что края, образующие границы между плоскими частями поверхности, выступают на данный чертеж. Вес и длина каждого ребра определяют разницу в уклонах поверхности по обе стороны от ребра, и условие, что каждая вершина находится в равновесии со своими соседями, эквивалентно условию, что эти различия уклонов заставляют поверхность встречаться с сам правильно в окрестности вершины. Положительные веса переводятся в выпуклые двугранные углы между двумя гранями кусочно-линейной поверхности, а отрицательные веса переводятся в вогнутые двугранные углы. И наоборот, каждая непрерывная кусочно-линейная поверхность возникает таким образом из равновесного напряжения. Если нарисован конечный плоский граф и задано равновесное напряжение таким образом, что все внутренние ребра чертежа имеют положительный вес, а все внешние ребра имеют отрицательный вес, то, преобразовав это напряжение в трехмерную поверхность таким образом, а затем заменяя плоскую поверхность, представляющую внешность графа, его дополнением в той же плоскости, мы получаем выпуклый многогранник с дополнительным свойством, что его перпендикулярная проекция на плоскость не имеет пересечений.[16][17]

Соответствие Максвелла – Кремоны было использовано для получения полиэдральных реализаций многогранных графов путем комбинирования его с плоским рисунок графика метод В. Т. Тутте, то Вложение Тутте. Метод Тутте начинается с фиксации одной грани многогранного графа в выпуклое положение в плоскости. Эта грань станет внешней гранью рисунка графика. Метод продолжается установкой системы линейных уравнений в координатах вершины, согласно которой каждая оставшаяся вершина должна быть помещена в среднее значение ее соседей. Тогда, как показал Тутте, эта система уравнений будет иметь единственное решение, в котором каждая грань графа изображена как выпуклый многоугольник.[18] В результате получается почти равновесное напряжение: если присвоить каждому внутреннему ребру вес по одному, то каждая внутренняя вершина чертежа будет находиться в равновесии. Однако не всегда можно присвоить отрицательные числа внешним ребрам, чтобы они тоже находились в равновесии. Такое назначение всегда возможно, когда внешняя грань представляет собой треугольник, и поэтому этот метод можно использовать для реализации любого многогранника. граф, имеющий треугольную грань. Если многогранный граф не содержит треугольной грани, его двойственный граф действительно содержит треугольник, а также является многогранным, поэтому можно реализовать двойственное таким образом, а затем реализовать исходный граф как полярный многогранник дуальной реализации.[19][20] Также возможно реализовать любой многогранный граф напрямую, выбрав внешней гранью любую грань с не более чем пятью вершинами (что существует во всех многогранных графах) и более тщательно выбрав фиксированную форму этой грани таким образом, чтобы Tutte вложение можно снять,[21] или используя инкрементный метод вместо метода Тутте, чтобы найти поднимаемый плоский чертеж, который не имеет равных весов для всех внутренних краев.[22]

Упаковка круга

Многогранник, полученный из упаковки кругов. Круги, представляющие вершины многогранника, являются их горизонтами на сфере, а круги, представляющие грани (двойные вершины), являются пересечениями сферы с плоскостями граней.

По одному из вариантов теорема об упаковке кругов, для каждого многогранного графа и его двойственный граф, существует система окружностей на плоскости или на любой сфере, представляющая вершины обоих графов, так что две соседние вершины в одном и том же графе представлены касательные круги, прямая и двойственная вершины, которые представляют вершину и грань, соприкасающиеся друг с другом, представлены ортогональными окружностями, а все остальные пары окружностей не пересекаются.[23] Из такого представления на сфере можно найти полиэдральную реализацию данного графа как пересечение набора полупространств, по одному для каждой окружности, представляющей дуальную вершину, с границей полупространства, содержащего окружность. Альтернативно и эквивалентно можно найти тот же многогранник, что и выпуклый корпус набора точек (его вершин) таким образом, что горизонт, видимый при просмотре сферы из любой вершины, равен окружности, соответствующей этой вершине. Сфера становится средняя сфера реализации: каждое ребро многогранника касается его в точке, где встречаются две касательные прямые окружности и две двойственные окружности, ортогональные прямым окружностям и касательные друг к другу.[24]

Реализации с дополнительными свойствами

Целочисленные координаты

Можно доказать более сильную форму теоремы Стейница, что любой многогранный граф может быть реализован выпуклым многогранником, у которого все координаты вершин являются целыми числами. Например, оригинальное доказательство Стейница, основанное на индукции, может быть усилено таким образом. Однако целые числа, полученные в результате этой конструкции, равны дважды экспоненциальный по количеству вершин данного многогранного графа. Записывая числа этой величины в двоичная запись потребует экспоненциального количества бит.[25]

Последующие исследователи обнаружили алгоритмы реализации на основе подъема, которые используют только O (п) бит на вершину.[21][26] Также можно ослабить требование, чтобы координаты были целыми числами, и назначить координаты таким образом, чтобы Икс-координаты вершин - различные целые числа в диапазоне [0,2п - 4], а две другие координаты являются действительными числами в диапазоне [0,1], так что каждое ребро имеет длину не менее единицы, а весь многогранник имеет объем O (п).[27] Известно, что некоторые многогранные графы могут быть реализованы на сетках только полиномиального размера; в частности, это верно для пирамид (реализации колесные графики ), призмы (реализации призматические графики ), и сложенные многогранники (реализации Аполлонические сети ).[28]

Равные склоны

А График Халина планарный граф, образованный из плоско-вложенных дерево (без вершин степени два), соединив листья дерева в цикл. Каждый граф Халина может быть реализован в виде многогранника, в котором этот цикл образует горизонтальную базовую грань, каждая другая грань расположена непосредственно над базовой гранью (как в многогранниках, реализованных посредством подъема), и каждая грань имеет одинаковый наклон. Эквивалентно прямой скелет базовой грани комбинаторно эквивалентно дереву, из которого образован граф Халина. Доказательство этого результата использует индукцию: любое корневое дерево может быть сведено к меньшему дереву, удалив листья из внутреннего узла, все дочерние элементы которого являются листьями, граф Халина, сформированный из меньшего дерева, имеет реализацию по предположению индукции, и это можно изменить эту реализацию, чтобы добавить любое количество дочерних листьев к узлу дерева, дочерние элементы которого были удалены.[29]

Определение формы лица

В любом многограннике, представляющем данный многогранный граф грамм, лица грамм точно циклы в грамм которые не разделяют грамм на два компонента: то есть удаление лицевого цикла из грамм оставляет остальную часть грамм как связный подграф. Таким образом, грани однозначно определяются из структуры графа. Еще одно усиление теоремы Стейница, сделанное Барнеттом и Грюнбаумом, утверждает, что для любого многогранного графа, любой грани графа и любого выпуклого многоугольника, представляющего эту грань, можно найти многогранная реализация всего графа, имеющая заданную форму для обозначенной грани. Это связано с теоремой Тутте, что любой многогранный граф можно нарисовать на плоскости со всеми выпуклыми гранями и любой заданной формой для его внешней грани. Однако планарный графические рисунки полученные методом Тутте не обязательно поднимаются до выпуклых многогранников. Вместо этого Барнетт и Грюнбаум доказывают этот результат индуктивным методом.[30] Также всегда возможно, учитывая многогранный граф грамм и произвольный цикл C, чтобы найти такую ​​реализацию, что C формирует силуэт реализации в рамках параллельная проекция.[31]

Касательные сферы

В Koebe –Андреев–Терстон теорема об упаковке кругов можно интерпретировать как еще одно усиление теоремы Стейница, что каждый 3-связный плоский граф может быть представлен как выпуклый многогранник таким образом, что все его ребра касаются одного и того же единичная сфера.[24] Выполняя тщательно подобранный Преобразование Мёбиуса упаковки окружностей перед преобразованием ее в многогранник, можно найти полиэдральную реализацию, которая реализует все симметрии нижележащего графа в том смысле, что каждый автоморфизм графа - симметрия полиэдральной реализации.[32][33] В более общем смысле, если грамм является многогранным графом и K любое гладкое трехмерное выпуклое тело, можно найти полиэдральное представление грамм в котором все ребра касаются K.[34]

Методы упаковки в окружности также можно использовать для характеристики графов многогранников, имеющих окружающая сфера или же вдохновлять. Характеристика включает веса ребер, ограниченные системами линейных неравенств. Эти веса соответствуют углам, образованным смежными окружностями в системе окружностей, образованных пересечениями граней многогранника с их описанной сферой или горизонтами вершин многогранника на его внутренней сфере.[35][36]

Связанные результаты

В Многогранник Силасси, невыпуклая полиэдральная реализация График Хивуда с топологией тор

В любом измерении выше трех алгоритмическая проблема Стейница (с учетом решетка, определим, является ли это решеткой граней выпуклый многогранник ) является полный для экзистенциальная теория реальности по теореме универсальности Рихтера-Геберта.[37] Однако, поскольку данный граф может соответствовать более чем одной решетке граней, трудно распространить этот результат о полноте на проблему распознавания графов 4-многогранников, и сложность этой проблемы остается открытой.

Исследователи также нашли теоретико-графические характеристики графиков некоторых специальных классов трехмерных невыпуклых многогранников.[38][39] и четырехмерные выпуклые многогранники.[40][41][42] Однако в обоих случаях общая проблема остается нерешенной. Действительно, даже проблема определения того, какие полные графики являются графами невыпуклых многогранников (кроме K4 для тетраэдра и K7 для Многогранник Часара ) остается нерешенным.[43]

Ласло Ловас показал соответствие многогранных представлений графов и матриц, реализующих Граф инвариантов Колена де Вердьера тех же графиков.[44]

Рекомендации

  1. ^ Вайсштейн, Эрик В. «Многогранный граф». MathWorld.
  2. ^ а б Бранко Грюнбаум, Выпуклые многогранники, 2-е издание, подготовлено Фолькером Кайбелем, Виктор Клее, и Гюнтер М. Циглер, 2003, ISBN  0-387-40409-0, ISBN  978-0-387-40409-7, 466с.
  3. ^ а б Лекции по многогранникам, к Гюнтер М. Циглер (1995) ISBN  0-387-94365-X , Глава 4 "Теорема Штейница для 3-многогранников", стр.103.
  4. ^ а б Стейниц, Эрнст (1922), "Polyeder und Raumeinteilungen", Encyclopädie der Mathematischen Wissenschaften, Полоса 3 (геометрии), стр. 1–139, Абгешлоссен, 31 августа 1916 г..
  5. ^ Зинель, Мариуш (1996), "Теорема Стейница и размерность векторного пространства", Формализованная математика, 5 (8): 423–428, CiteSeerX  10.1.1.79.1707.
  6. ^ Киркпатрик, Дэвид; Мишра, Бхубанешвар; Яп, Чи-Кенг (1992), "Количественные теоремы Стейница с приложениями к многоязычному схватыванию", Дискретная и вычислительная геометрия, 7 (1): 295–318, Дои:10.1007 / BF02187843.
  7. ^ Розенталь, Питер (1987), "Замечательная теорема Леви и Стейница", Американский математический ежемесячный журнал, 94 (4): 342–351, Дои:10.2307/2323094, JSTOR  2323094.
  8. ^ Банащик, Войцех (1991). «Глава 3.10 Теорема Леви-Стейница». Аддитивные подгруппы топологических векторных пространств. Конспект лекций по математике. 1466. Берлин: Springer-Verlag. С. viii + 178. ISBN  3-540-53917-4. МИСТЕР  1119302.
  9. ^ Кадец, В. М .; Кадец, М. И. (1991). "Глава 6 Теорема Стейница и B-выпуклость ». Перестановки рядов в банаховых пространствах. Переводы математических монографий. 86 (Перевод Гарольда Макфадена с русскоязычного (Тарту) изд. 1988 г.). Провиденс, Род-Айленд: Американское математическое общество. С. iv + 123. ISBN  0-8218-4546-2. МИСТЕР  1108619.
  10. ^ Кадец Михаил И .; Кадец, Владимир М. (1997). »Глава 2.1 Теорема Стейница о диапазоне сумм ряда, Глава 7 Теорема Стейница и B-выпуклость ». Ряды в банаховых пространствах: условная и безусловная сходимость. Теория операторов: достижения и приложения. 94 (Перевод Андрея Якоба из русскоязычной ред.). Базель: Birkhäuser Verlag. С. viii + 156. ISBN  3-7643-5401-1. МИСТЕР  1442255.
  11. ^ Балински, М.Л. (1961), «О графическом строении выпуклых многогранников в п-Космос", Тихоокеанский математический журнал, 11 (2): 431–434, Дои:10.2140 / pjm.1961.11.431, МИСТЕР  0126765.
  12. ^ Епифанов, Г. В. (1966), "Приведение плоского графа к ребру преобразованиями звезда-треугольник", Доклады Академии Наук СССР, 166: 19–22, МИСТЕР  0201337.
  13. ^ Truemper, K. (1989), "О сокращении треугольника для плоских графов", Журнал теории графов, 13 (2): 141–148, Дои:10.1002 / jgt.3190130202, МИСТЕР  0994737.
  14. ^ Чанг, Сянь-Чжи; Эриксон, Джефф (27 сентября 2015 г.), Электрическая редукция, гомотопические движения и дефект.
  15. ^ Барнетт, Дэвид У .; Грюнбаум, Бранко (1969), «О теореме Стейница о выпуклых 3-многогранниках и о некоторых свойствах плоских графов», Многогранность теории графов (Proc. Conf., Western Mich. Univ., Kalamazoo, Mich., 1968), Springer, стр. 27–40, МИСТЕР  0250916.
  16. ^ Максвелл, Дж. Клерк (1864), «О взаимных фигурах и диаграммах сил», Философский журнал, 4-я серия, 27: 250–261.
  17. ^ Уайтли, Уолтер (1982), "Движения и напряжения спроецированных многогранников", Структурная топология, 7: 13–38, МИСТЕР  0721947.
  18. ^ Тутте, В. Т. (1963), «Как нарисовать график», Труды Лондонского математического общества, 13: 743–767, Дои:10.1112 / плмс / с3-13.1.743, МИСТЕР  0158387.
  19. ^ Онн, Шмуэль; Штурмфельс, Бернд (1994), "Количественная теорема Стейница", Beiträge zur Algebra und Geometrie, 35 (1): 125–129, МИСТЕР  1287206.
  20. ^ Идс, Питер; Гарван, Патрик (1996), "Рисование напряженных плоских графов в трех измерениях", Графический рисунок (GD '95), Конспект лекций по информатике, 1027, Springer, стр. 212–223, Дои:10.1007 / bfb0021805.
  21. ^ а б Рибо Мор, Арес; Роте, Гюнтер; Шульц, Андре (2011), "Вложения 3-многогранников в малую сетку", Дискретная и вычислительная геометрия, 45 (1): 65–87, arXiv:0908.0488, Дои:10.1007 / s00454-010-9301-0, S2CID  10141034.
  22. ^ Хробак, Марек; Гудрич, Майкл Т.; Тамассия, Роберто (1996), «Выпуклые рисунки графиков в двух и трех измерениях», Материалы 12-го ACM Симпозиум по вычислительной геометрии (SoCG '96), ACM, стр. 319–328, Дои:10.1145/237218.237401, S2CID  1015103.
  23. ^ Brightwell, Graham R .; Шайнерман, Эдвард Р. (1993), "Представления плоских графов", Журнал SIAM по дискретной математике, 6 (2): 214–229, Дои:10.1137/0406017.
  24. ^ а б Циглер, Гюнтер М. (2007), «Выпуклые многогранники: экстремальные конструкции и ж-векторные формы. Раздел 1.3: Теорема Стейница через упаковку кругов », Миллер, Эзра; Райнер, Виктор; Штурмфельс, Бернд (ред.), Геометрическая комбинаторика, IAS / Серия математики Парк-Сити, 13, Американское математическое общество, стр. 628–642, ISBN  978-0-8218-3736-8.
  25. ^ Венкатасубраманян, Суреш (2006), Планарные графы и теорема Стейница.
  26. ^ Бучин, Кевин; Шульц, Андре (2010), «О количестве остовных деревьев, которые может иметь планарный граф», Алгоритмы - 18-й ежегодный европейский симпозиум (ESA 2010), Конспект лекций по информатике, 6346, Springer-Verlag, стр. 110–121, Bibcode:2010LNCS.6346 ..... D, Дои:10.1007/978-3-642-15775-2, ISBN  978-3-642-15774-5.
  27. ^ Шульц, Андре (2011), «Рисование 3-многогранников с хорошим разрешением вершин» (PDF), Журнал графических алгоритмов и приложений, 15 (1): 33–52, Дои:10.7155 / jgaa.00216.
  28. ^ Демейн, Эрик Д.; Шульц, Андре (2011), "Вложение многогранников с накоплением в сетку полиномиального размера", Proc. 22-й симпозиум ACM-SIAM. Дискретные алгоритмы (SODA '11), стр. 1177–1187.
  29. ^ Айхольцер, Освин; Ченг, Ховард; Devadoss, Satyan L .; Хакл, Томас; Хубер, Стефан; Ли, Брайан; Ристески, Андрей (2012), "Что делает дерево прямым скелетом?" (PDF), Труды 24-й Канадской конференции по вычислительной геометрии (CCCG'12).
  30. ^ Барнетт, Дэвид У .; Грюнбаум, Бранко (1970), «Задание формы лица», Тихоокеанский математический журнал, 32 (2): 299–306, Дои:10.2140 / pjm.1970.32.299, МИСТЕР  0259744.
  31. ^ Барнетт, Дэвид В. (1970), "Проекции 3-многогранников", Израильский математический журнал, 8 (3): 304–308, Дои:10.1007 / BF02771563, S2CID  120791830.
  32. ^ Харт, Джордж У. (1997), «Вычисление канонических многогранников», Математика в образовании и исследованиях, 6 (3): 5–10.
  33. ^ Берн, Маршалл; Эппштейн, Дэвид (2001), «Оптимальные преобразования Мёбиуса для визуализации информации и построения сеток», Proc. 7-й Worksh. Алгоритмы и структуры данных (WADS 2001), Лект. Примечания Комп. Наук, 2125, Springer, стр. 14–25, arXiv:cs / 0101006, Дои:10.1007/3-540-44634-6_3, S2CID  3266233.
  34. ^ Шрамм, Одед (1992), «Как запереть яйцо», Inventiones Mathematicae, 107 (3): 543–560, Bibcode:1992InMat.107..543S, Дои:10.1007 / BF01231901, МИСТЕР  1150601, S2CID  189830473.
  35. ^ Ривин, Игорь (1996), "Характеристика идеальных многогранников в трехмерном гиперболическом пространстве", Анналы математики, Вторая серия, 143 (1): 51–70, Дои:10.2307/2118652, JSTOR  2118652, МИСТЕР  1370757.
  36. ^ Дилленкур, Майкл Б.; Смит, Уоррен Д. (1996), «Теоретико-графовые условия вписываемости и реализуемости Делоне», Дискретная математика, 161 (1–3): 63–77, Дои:10.1016 / 0012-365X (95) 00276-3, МИСТЕР  1420521.
  37. ^ Рихтер-Геберт, Юрген (1996). Пространства реализации многогранников. Конспект лекций по математике. 1643. Springer-Verlag. ISBN  978-3-540-62084-6.
  38. ^ Хонг, Сок-Хи; Нагамочи, Хироши (2011), «Распространение теоремы Стейница на восходящие звездообразные многогранники и сферические многогранники», Алгоритмика, 61 (4): 1022–1076, Дои:10.1007 / s00453-011-9570-x, МИСТЕР  2852056, S2CID  12622357.
  39. ^ Эппштейн, Дэвид; Мамфорд, Елена (2014), "Теоремы Стейница для простых ортогональных многогранников", Журнал вычислительной геометрии, 5 (1): 179–244, МИСТЕР  3259910.
  40. ^ Слепой, Росвита; Мани-Левицка, Питер (1987), "Головоломки и изоморфизмы многогранников", Aequationes Mathematicae, 34 (2–3): 287–297, Дои:10.1007 / BF01830678, МИСТЕР  0921106, S2CID  120222616.
  41. ^ Калаи, Гил (1988), "Простой способ отличить простой многогранник от его графика", Журнал комбинаторной теории, Серия А, 49 (2): 381–383, Дои:10.1016/0097-3165(88)90064-7, МИСТЕР  0964396.
  42. ^ Эппштейн, Дэвид (2016), «Верхушки деревьев и их графики», Proc. 27-й симпозиум ACM-SIAM. Дискретные алгоритмы (SODA '16).
  43. ^ Циглер, Гюнтер М. (2008), «Полиэдральные поверхности высокого рода», Дискретная дифференциальная геометрия, Обервольфахские семинары, 38, Springer, стр. 191–213, arXiv:математика / 0412093, Дои:10.1007/978-3-7643-8621-4_10, ISBN  978-3-7643-8620-7, МИСТЕР  2405667, S2CID  15911143.
  44. ^ Ловас, Ласло (2001), "Представления Штейница многогранников и число Колена де Вердьера", Журнал комбинаторной теории, Серия B, 82 (2): 223–236, Дои:10.1006 / jctb.2000.2027, МИСТЕР  1842113.