Логическая двусмысленность - Logical biconditional
В логика и математика, то логическая двусмысленность, иногда известный как материал бикондиционный, это логическая связка используется для соединения двух утверждений и сформировать заявление » если и только если ", куда известен как предшествующий, и в последующий.[1][2][3] Это часто сокращается как " если только ".[4] Оператор обозначается двуглавой стрелкой (↔[5] или ⇔[6]), префикс E "Epq" (в Обозначение Лукасевича или же Обозначение Бохенского ), знак равенства (=), знак эквивалентности (≡)[4], или же EQV. Это логически эквивалентно обоим и , а XNOR (исключая ни) логический оператор, что означает «оба или ни один».
Семантически единственный случай, когда логическая двусмысленность отличается от материальный условный это случай, когда гипотеза ложна, но вывод верен. В этом случае результат будет истинным для условного, но ложным для двусмысленного.[2]
В концептуальной интерпретации означает "Все есть и все есть 's ". Другими словами, наборы и совпадают: они идентичны. Однако это не означает, что и должны иметь то же значение (например, может быть "равносторонним трехугольником" и может быть «равносторонний треугольник»). Когда формулируется как предложение, антецедент - это предмет а следствием является предикат из универсальный утвердительный предложение (например, во фразе «все люди смертны», «люди» - подлежащее, а «смертные» - сказуемое).
В пропозициональной интерпретации Значит это подразумевает и подразумевает ; другими словами, предложения логически эквивалентный в том смысле, что оба они либо вместе верны, либо вместе ложны. Опять же, это не означает, что они должны иметь то же значение, что и может быть "треугольник ABC имеет две равные стороны" и может быть «треугольник ABC имеет два равных угла». В общем, антецедент - это предпосылка, или причина, а следствием является последствие. Когда импликация переводится гипотетический (или же условный) суждение, антецедент называется гипотеза (или условие), а консеквент называется Тезис.
Распространенный способ демонстрации двусмысленности формы показать, что и отдельно (из-за его эквивалентности конъюнкции двух обратных условные[2]). Еще один способ продемонстрировать то же двусловное условие - продемонстрировать, что и .[1]
Когда оба члена двусмысленного выражения являются предложениями, его можно разделить на два условных предложения, одно из которых называется теорема а другой его взаимный.[нужна цитата ] Таким образом, всякий раз, когда теорема и обратная теорема верны, у нас есть двоякое условие. Простая теорема приводит к импликации, антецедентом которой является гипотеза и чьим следствием является Тезис теоремы.
Часто говорят, что гипотеза - это достаточное условие диссертации, и эта диссертация является необходимое условие гипотезы. То есть достаточно, чтобы гипотеза была верной, чтобы тезис был верным, в то время как необходимо, чтобы тезис был верным, если гипотеза верна. Когда теорема и обратная теорема верны, ее гипотеза называется гипотезой. необходимое и достаточное условие диссертации. То есть гипотеза является одновременно причиной и следствием тезиса.
Определение
Логическое равенство (также известный как двусмысленный) - это операция на двух логические значения, обычно значения двух предложения, что дает значение истинный тогда и только тогда, когда оба операнда ложны или оба операнда истинны.[2]
Таблица истинности
Ниже приводится таблица истинности для (также пишется как , , или же P EQ Q):
| Т | Т | Т |
| Т | F | F |
| F | Т | F |
| F | F | Т |
Если задействовано более двух утверждений, их сочетание с может быть двусмысленным. Например, утверждение
можно интерпретировать как
- ,
или может быть истолковано как утверждение, что все находятся совместно верно или совместно ложно:
Как оказалось, эти два утверждения одинаковы только тогда, когда задействовано ноль или два аргумента. Фактически, следующие таблицы истинности показывают один и тот же битовый шаблон только в строке без аргументов и в строках с двумя аргументами:

означал как эквивалент
Центральная диаграмма Венна ниже,
и линия (ABC) в этой матрице
представляют собой ту же операцию.

означал как сокращение для
Диаграмма Венна ниже,
и линия (ABC) в этой матрице
представляют собой ту же операцию.
Левая диаграмма Венна ниже, а линии (AB) в этих матрицах представляют собой одну и ту же операцию.
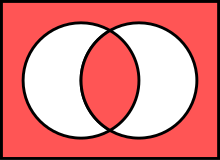
Диаграммы Венна
Красные области означают истину (как в ![]() за и ).
за и ).
|
|
|
Характеристики
Коммутативность: Да
Ассоциативность: Да
 |  |  |  |  |
Распределительность: Biconditional не распространяется ни на одну двоичную функцию (даже на себя), но логическая дизъюнкция распределяет над двусмысленным.
идемпотентность: Нет
Монотонность: Нет
 |  |  |  |
Сохранение истины: Да
Когда все входы верны, выход верен.
Сохранение лжи: Нет
Когда все входы ложны, выход не является ложным.
Спектр Уолша: (2,0,0,2)
Нелинейность: 0 (функция линейная)
Правила вывода
Как и все связки в логике первого порядка, у двусмысленного выражения есть правила вывода, которые регулируют его использование в формальных доказательствах.
Двузначное введение
Бикондиционное введение позволяет заключить, что если B следует из A, а A следует из B, то A если и только если Б.
Например, из утверждений «если я дышу, значит я жив» и «если я жив, то я дышу», можно сделать вывод, что «я дышу тогда и только тогда, когда я» м жив »или, что эквивалентно:« Я жив, если и только если я дышу ». Или более схематично:
Б → А А → Б ∴ А ↔ Б
Б → А А → Б ∴ Б ↔ А
Двуусловное исключение
Двуусловное исключение позволяет вывести условный от двусмысленного: если A ↔ B истинно, то можно вывести либо A → B или B → А.
Например, если правда, что я дышу если и только если Я жив, значит это правда если Я дышу, значит, я жив; Точно так же это правда, что если Я жив, значит, я дышу. Или более схематично:
А ↔ Б ∴ А → Б
А ↔ Б ∴ B → A
Разговорное использование
Один из недвусмысленных способов сформулировать двусмысленное выражение на простом английском языке - это принять форму "б если а и а если б"- если стандартная форма"а если и только если б"не используется. Чуть более формально можно сказать, что"б подразумевает а и а подразумевает б", или же "а необходимо и достаточно для б".[1] Простое английское «if '» иногда может использоваться как двоякое (особенно в контексте математического определения[7]). В этом случае при интерпретации этих слов необходимо учитывать окружающий контекст.
Например, утверждение «Я куплю вам новый кошелек, если он вам понадобится» может быть истолковано как двоякое условие, поскольку говорящий не предполагает правильного результата покупки кошелька независимо от того, нужен кошелек или нет (как в условном). Однако «облачно, если идет дождь», как правило, не подразумевается как двоякое условие, поскольку может быть облачно, даже если нет дождя.
Смотрите также
- Если и только если
- Логическая эквивалентность
- Логическое равенство
- XNOR ворота
- Двуусловное исключение
- Двуусловное введение
Рекомендации
- ^ а б c «Окончательный глоссарий высшего математического жаргона - если и только если». Математическое хранилище. 2019-08-01. Получено 2019-11-25.
- ^ а б c d Пейл, Тимоти. «Условные и двусмысленные». web.mnstate.edu. Получено 2019-11-25.
- ^ Бреннан, Джозеф Г. (1961). Справочник по логике (2-е изд.). Харпер и Роу. п. 81.
- ^ а б Вайсштейн, Эрик В. "Iff". mathworld.wolfram.com. Получено 2019-11-25.
- ^ «Двуусловные утверждения | Математические вкусности». www.mathgoodies.com. Получено 2019-11-25.
- ^ «2.4: Двухусловные утверждения». Математика LibreTexts. 2018-04-25. Получено 2019-11-25.
- ^ Собственно, таков стиль, принятый Руководство по стилям в математике в Википедии.
внешняя ссылка
 СМИ, связанные с Логическая двусмысленность в Wikimedia Commons
СМИ, связанные с Логическая двусмысленность в Wikimedia Commons
В этой статье использованы материалы с сайта Biconditional на PlanetMath, который находится под лицензией Лицензия Creative Commons Attribution / Share-Alike.





























































