Гексомино - Hexomino

А гексомино (или 6-омино) это полимино порядка 6, то есть многоугольник в самолет состоит из 6 одинаковых по размеру квадраты соединены встык.[1] Название этого типа фигур состоит из приставки шестнадцатеричный (а) -. Когда вращения и размышления не считаются отдельными формами, есть 35 другой свободный гексомино. Когда отражения считаются отчетливыми, есть 60 односторонний гексомино. Когда вращения также считаются отдельными, есть 216 исправлено гексомино.[2][3]
Симметрия
На рисунке выше показаны все 35 возможных бесплатных гексомино, окрашенных в соответствии с их цветом. группы симметрии:
- У двадцати серых гексомино нет симметрия. Их группа симметрии состоит только из отображение идентичности.
- Шесть красных гексомино имеют ось зеркальная симметрия параллельно линиям сетки. Их группа симметрии состоит из двух элементов: идентичности и отражения в линии, параллельной сторонам квадратов.
- Два зеленых гексомино имеют ось зеркальной симметрии под углом 45 ° к линиям сетки. Их группа симметрии состоит из двух элементов: тождества и диагонального отражения.
- Пять синих гексомино обладают точечной симметрией, также известной как вращательная симметрия порядка 2. Их группа симметрии состоит из двух элементов: идентичности и поворота на 180 °.
- Два фиолетовых гексомино имеют две оси зеркальной симметрии, обе параллельны линиям сетки (таким образом, одна горизонтальная ось и одна вертикальная ось). Их группа симметрии состоит из четырех элементов. Это группа диэдра порядка 2, также известный как Кляйн четыре группы.
Если отражения гексомино считаются отдельными, как в случае односторонних гексомино, то каждая из указанных выше категорий первой и четвертой будет вдвое больше, что приведет к дополнительным 25 гексомино, всего 60. Если вращения также считаются отдельными, тогда гексомино из первой категории засчитываются восьмикратно, из следующих трех категорий засчитываются четырехкратно, а из последней категории засчитываются дважды. В результате получается 20 × 8 + (6 + 2 + 5) × 4 + 2 × 2 = 216 фиксированных гексомино.
Упаковка и укладка
Каждое из 35 гексомино удовлетворяет требованиям Критерий Конвея; следовательно, каждое гексомино способно разбить плоскость.[4]
Хотя полный набор из 35 гексомино состоит из 210 квадратов, их невозможно упаковать в одно целое. прямоугольник. (Такое расположение возможно с 12 пентамино которые могут быть упакованы в любой из прямоугольников 3 × 20, 4 × 15, 5 × 12 и 6 × 10.) Простой способ продемонстрировать, что такая упаковка гексомино невозможна, - это использовать паритет аргумент. Если гексомино положить на шахматная доска шаблона, то 11 гексомино покроют четное количество черных квадратов (либо 2 белых и 4 черных, либо наоборот), а остальные 24 гексомино покроют нечетное число черных квадратов (3 белых и 3 черных). В целом, при любом расположении будет покрыто четное количество черных квадратов. Однако любой прямоугольник из 210 квадратов будет иметь 105 черных квадратов и 105 белых квадратов, и поэтому не может быть покрыт 35 гексомино.
Однако есть и другие простые фигуры из 210 квадратов, которые можно заполнить гексомино. Например, квадрат 15 × 15 с удаленным из центра прямоугольником 3 × 5 имеет 210 квадратов. При расцветке шахматной доски он имеет 106 белых и 104 черных квадрата (или наоборот), поэтому паритет не препятствует упаковке, и упаковка действительно возможна.[5] Также возможно, чтобы два набора фигур уместились в прямоугольник размера 420 или для набора из 60 односторонних гексомино (18 из которых покрывают четное количество черных квадратов), чтобы поместиться в прямоугольник размера 360.[6]
Многогранные сетки для куба
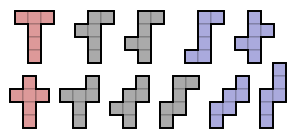
А многогранная сетка для куб обязательно является гексомино, причем 11 гексомино (показано справа) на самом деле являются сетями. Они появляются справа, снова окрашенные в соответствии с их группами симметрии.
Полиэдрическая сетка для куба не может содержать ни О-тетромино, ни I-пентамино, U-пентамино или V-пентамино.
использованная литература
- ^ Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02444-8.
- ^ Вайсштейн, Эрик В. «Гексомино». Из MathWorld - веб-ресурса Wolfram. Получено 2008-07-22.
- ^ Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика. 36: 191–203. Дои:10.1016 / 0012-365X (81) 90237-5.
- ^ Роадс, Гленн С. (2003). Плоские мозаики и поиск апериодического прототила. Кандидатская диссертация, Университет Рутгерса.
- ^ Mathematische Basteleien: Hexominos (по-английски)
- ^ Конструкции Hexomino
