Гептомино - Heptomino

А гептомино (или 7-омино) это полимино порядка 7, то есть многоугольник в самолет состоит из 7 одинаковых по размеру квадраты соединены встык.[1] Название этого типа фигур состоит из приставки гепта)-. Когда вращения и размышления не считаются отдельными формами, есть 108 другой свободный гептомино. Когда отражения считаются отчетливыми, есть 196 односторонний гептомино. Когда вращения также считаются отдельными, существует 760 исправлено гептомино.[2][3]
Симметрия
На рисунке показаны все возможные бесплатные гептамино, раскрашенные в соответствии с их группы симметрии:
- 84 гептомино (окрашены в серый цвет) не имеют симметрия. Их группа симметрии состоит только из отображение идентичности.
- 9 гептомино (окрашены в красный цвет) имеют ось симметрия отражения по линиям сетки. Их группа симметрии состоит из двух элементов: тождества и отражения на линии, параллельной сторонам квадратов.
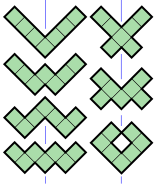
- 7 гептомино (окрашены в зеленый цвет) имеют ось симметрии отражения под углом 45 ° к линиям сетки. Их группа симметрии состоит из двух элементов: тождества и диагонального отражения.
- 4 гептомино (окрашены в синий цвет) имеют точечную симметрию, также известную как вращательная симметрия порядка 2. Их группа симметрии состоит из двух элементов: идентичности и поворота на 180 °.
- 3 гептомино (окрашены в фиолетовый цвет) имеют две оси симметрии отражения, обе совмещенные с линиями сетки. Их группа симметрии состоит из четырех элементов: идентичности, двух отражений и поворота на 180 °. Это группа диэдра порядка 2, также известный как Кляйн четыре группы.
- 1 гептомино (оранжевого цвета) имеет две оси симметрии отражения, обе совмещенные с диагоналями. Его группа симметрии также состоит из четырех элементов. Его группа симметрии также является группой диэдра порядка 2 с четырьмя элементами.
Если отражения гептомино считаются отдельными, как в случае односторонних гептомино, то каждая из указанных выше категорий первой и четвертой будет вдвое больше, что приведет к дополнительным 88 гептомино, в общей сложности 196. Если вращения также считаются отдельными, затем гептомино из первой категории засчитывается восьмикратно, из следующих трех категорий засчитывается четырехкратно, а из последних двух категорий засчитывается дважды. Это приводит к 84 × 8 + (9 + 7 + 4) × 4 + (3 + 1) × 2 = 760 фиксированных гептомино.
Упаковка и укладка
Из 108 бесплатных гептомино 101 удовлетворяет Критерий Конвея и еще 3 могут образовать заплатку, удовлетворяющую критерию. Таким образом, только 4 гептомино не удовлетворяют критерию, и фактически эти 4 не могут составить мозаику плоскости.[4]
 Четыре гептомино, неспособные уложить плоскость, включая одно гептомино с отверстием.
Четыре гептомино, неспособные уложить плоскость, включая одно гептомино с отверстием.
Хотя полный набор из 108 бесплатных гептомино состоит из 756 квадратов, это невозможно. плитка а прямоугольник с этим набором. Доказательство этого тривиально, поскольку есть одно гептомино с дыркой.[5] Также невозможно упаковать их в прямоугольник из 757 квадратов с отверстием в один квадрат, потому что 757 - простое число.
Однако набор из 107 односвязный свободные гептомино, то есть те, которые не имеют дыры, могут выложить прямоугольник 7 на 107 (квадрат 749).[6] Кроме того, полный набор бесплатных гептомино может размещать три прямоугольника размером 11 на 23 (253 квадратных), каждый с одним квадратным отверстием в центре; полный набор также может выложить двенадцать квадратов 8 на 8 (64 квадратных) с отверстием в один квадрат в «центре».[7]
использованная литература
- ^ Голомб, Соломон В. (1994). Полимино (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02444-8.
- ^ Вайсштейн, Эрик В. «Гептомино». Из MathWorld - веб-ресурса Wolfram. Получено 2008-07-22.
- ^ Редельмайер, Д. Хью (1981). «Подсчет полимино: еще одна атака». Дискретная математика. 36 (2): 191–203. Дои:10.1016 / 0012-365X (81) 90237-5.
- ^ Роадс, Гленн С. (2005). «Плоские мозаики из полимино, полигексов и полиалмазов». Журнал вычислительной и прикладной математики. 174 (2): 329–353. Дои:10.1016 / j.cam.2004.05.002.
- ^ Грюнбаум, Бранко; Шепард, Г. К. (1987). Плитки и узоры. Нью-Йорк: В. Х. Фриман и компания. ISBN 0-7167-1193-1.
- ^ «Полимино: еще больше гептомино!»
- ^ Изображение, «Невероятное решение гептомино Патрика Хэмлина», от Материал добавлен с февраля по август 2001 г. на MathPuzzzle.com