Касательное пространство - Tangent space
В математика, то касательное пространство из многообразие облегчает обобщение векторов из аффинные пространства к общим многообразиям, поскольку в последнем случае нельзя просто вычесть две точки, чтобы получить вектор, который дает смещение из одной точки в другую.
Неформальное описание

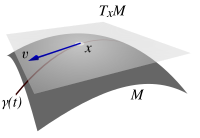
В дифференциальная геометрия, можно прикрепить к каждой точке из дифференцируемое многообразие а касательное пространство- настоящий векторное пространство который интуитивно содержит возможные направления, в которых можно по касательной . Элементы касательного пространства при называются касательные векторы в . Это обобщение понятия связанный вектор в Евклидово пространство. В измерение касательного пространства в каждой точке связаны коллектор такой же, как у многообразие сам.
Например, если данное многообразие является -сфера, то можно представить касательное пространство в точке как плоскость, которая касается сферы в этой точке и является перпендикуляр к радиусу сферы через точку. В более общем смысле, если заданное многообразие рассматривается как встроенный подмногообразие из Евклидово пространство, то можно буквально так представить касательное пространство. Это был традиционный подход к определению параллельный транспорт. Многие авторы в дифференциальная геометрия и общая теория относительности используй это. [1] [2] Более строго, это определяет аффинное касательное пространство, которое отличается от пространства касательных векторов, описываемого современной терминологией.
В алгебраическая геометрия, напротив, существует внутреннее определение касательное пространство в точке из алгебраическое многообразие что дает векторное пространство с размерностью не менее сам. Точки при котором размерность касательного пространства в точности равна размерности называются неособый точки; остальные называются единственное число точки. Например, кривая, которая пересекает себя, не имеет уникальной касательной в этой точке. Особые точки это те, в которых «тест на многообразие» не проходит. Видеть Касательное пространство Зарисского.
После введения касательных пространств многообразия можно определить векторные поля, которые являются абстракциями поля скоростей частиц, движущихся в пространстве. Векторное поле плавно присоединяет к каждой точке многообразия вектор из касательного пространства в этой точке. Такое векторное поле служит для определения обобщенного обыкновенное дифференциальное уравнение на многообразии: решение такого дифференциального уравнения является дифференцируемым изгиб на многообразии, производная которого в любой точке равна касательному вектору, прикрепленному к этой точке векторным полем.
Все касательные пространства многообразия могут быть «склеены вместе», чтобы сформировать новое дифференцируемое многообразие с удвоенной размерностью исходного многообразия, называемое касательный пучок коллектора.
Формальные определения
Неформальное описание выше полагается на способность многообразия быть вложенным в окружающее векторное пространство. так что касательные векторы могут «торчать» из коллектора в окружающее пространство. Однако удобнее определять понятие касательного пространства исключительно на основе самого многообразия.[3]
Существуют различные эквивалентные способы определения касательных пространств многообразия. Хотя определение с помощью скорости кривых интуитивно является самым простым, с ним также наиболее сложно работать. Ниже описаны более элегантные и абстрактные подходы.
Определение через касательные кривые
В картине вложенного многообразия касательный вектор в точке считается скорость из изгиб проходя через точку . Таким образом, мы можем определить касательный вектор как класс эквивалентности кривых, проходящих через будучи касательными друг к другу .
Предположим, что это многообразие () и что . Выберите карта координат , куда является открытое подмножество из содержащий . Предположим далее, что две кривые с даны так, что оба дифференцируемы в обычном смысле (мы называем их дифференцируемые кривые, инициализированные в ). потом и как говорят эквивалент в тогда и только тогда, когда производные и в совпадают. Это определяет отношение эквивалентности на множестве всех дифференцируемых кривых, инициализированных в , и классы эквивалентности таких кривых известны как касательные векторы из в . Класс эквивалентности любой такой кривой обозначается . В касательное пространство из в , обозначаемый , тогда определяется как множество всех касательных векторов в ; не зависит от выбора координатной карты .
Чтобы определить операции в векторном пространстве на , мы используем диаграмму и определим карта к куда . Опять же, нужно проверить, что эта конструкция не зависит от конкретной карты. и кривая используется, а на самом деле это не так.
Карта оказывается биективный и может использоваться для переноса операций в векторном пространстве на к , превратив последний набор в -мерное вещественное векторное пространство.
Определение через производные
Предположим теперь, что это многообразие. Действительная функция Говорят, что принадлежит тогда и только тогда, когда для каждой координатной карты , карта бесконечно дифференцируемо. Обратите внимание, что настоящий ассоциативная алгебра с уважением к точечный продукт и сумма функций и скалярное умножение.
Выберите точку . А происхождение в определяется как линейная карта что удовлетворяет тождеству Лейбница
который создан по образцу правило продукта исчисления.
(Для каждой одинаково постоянной функции следует, что ).
Если мы определим сложение и скалярное умножение на множестве производных в к
- и
- ,
то мы получаем реальное векторное пространство, которое мы определяем как касательное пространство из в .
Обобщения
Возможны обобщения этого определения, например, на комплексные многообразия и алгебраические многообразия. Однако вместо изучения выводов из полной алгебры функций, вместо этого нужно работать на уровне микробы функций. Причина в том, что структурный пучок может и не быть отлично для таких конструкций. Например, пусть быть алгебраическим многообразием с структурный пучок . Тогда Касательное пространство Зарисского в какой-то момент это собрание всех -деривации , куда это наземное поле и это стебель из в .
Эквивалентность определений
За и дифференцируемая кривая такой, что определять (где производная берется в обычном смысле, потому что это функция от к ). Можно констатировать, что вывод в точке и эти эквивалентные кривые дают тот же вывод. Таким образом, для класса эквивалентности мы можем определить где кривая был выбран произвольно. Карта изоморфизм векторного пространства между пространством классов эквивалентности и выводов в точке
Определение через котангенс
Снова начнем с многообразие и точка . Рассмотрим идеальный из состоящий из всех гладких функций исчезновение в , т.е. . потом и - вещественные векторные пространства, а можно определить как двойное пространство из факторное пространство . Это последнее фактор-пространство также известно как котангенс пространство из в .
Хотя это определение является наиболее абстрактным, его легче всего перенести на другие настройки, например, на разновидности рассматривается в алгебраическая геометрия.
Если это вывод на , тогда для каждого , что обозначает рождает линейную карту . Наоборот, если является линейным отображением, то определяет вывод в . Это дает эквивалентность между касательными пространствами, определенными с помощью производных, и касательными пространствами, определенными с помощью кокасательных пространств.
Характеристики
Если открытое подмножество , тогда это многообразие естественным образом (примем координатные карты карты идентичности на открытых подмножествах ), и все касательные пространства естественным образом отождествляются с .
Касательные векторы как производные по направлению
Другой способ думать о касательных векторах - это как направленные производные. Учитывая вектор в , определяется соответствующая производная по направлению в точке к
Это отображение, естественно, является производным от . Кроме того, каждый вывод в точке в имеет такую форму. Следовательно, существует взаимно однозначное соответствие между векторами (рассматриваемыми как касательные векторы в точке) и производными в точке.
Поскольку касательные векторы к общему многообразию в точке могут быть определены как производные в этой точке, естественно думать о них как о производных по направлениям. В частности, если является касательным вектором к в какой-то момент (рассматривается как производная), затем определите производную по направлению в направлении к
Если мы подумаем о как начальная скорость дифференцируемой кривой инициализирован в , т.е. , тогда вместо этого определите к
Базис касательного пространства в точке
Для многообразие , если график дается с , то можно определить упорядоченный базис из к
Тогда для каждого касательного вектора , надо
Следовательно, эта формула выражает как линейную комбинацию базисных касательных векторов определяется координатной картой .[4]
Производная от карты
Каждая гладкая (или дифференцируемая) карта между гладкими (или дифференцируемыми) многообразиями индуцирует естественные линейные карты между соответствующими касательными пространствами:
Если касательное пространство определяется через дифференцируемые кривые, то это отображение определяется как
Если вместо этого касательное пространство определяется с помощью производных, то это отображение определяется как
Линейная карта называется по-разному производная, полная производная, дифференциал, или же продвигать из в . Это часто выражается с использованием множества других обозначений:
В некотором смысле производная является наилучшим линейным приближением к возле . Обратите внимание, что когда , то карта совпадает с обычным понятием дифференциал функции . В местные координаты производная от дается Якобиан.
Важный результат относительно производной карты следующий:
- Теорема. Если это локальный диффеоморфизм в в , тогда линейный изоморфизм. Наоборот, если является изоморфизмом, то существует открытый район из такой, что карты диффеоморфно на свой образ.
Это обобщение теорема об обратной функции отображать между многообразиями.
Смотрите также
- Экспоненциальная карта
- Векторное пространство
- Дифференциальная геометрия кривых
- Координатно-индуцированный базис
- Котангенс пространство
Примечания
- ^ ду Карму, Манфредо П. (1976). Дифференциальная геометрия кривых и поверхностей.. Прентис-Холл.:
- ^ Дирак, Поль А. М. (1996) [1975]. Общая теория относительности. Издательство Принстонского университета. ISBN 0-691-01146-X.
- ^ Крис Дж. Ишем (1 января 2002 г.). Современная дифференциальная геометрия для физиков. Союзные издатели. С. 70–72. ISBN 978-81-7764-316-9.
- ^ Лерман, Евгений. «Введение в дифференциальную геометрию» (PDF). п. 12.
Рекомендации
- Ли, Джеффри М. (2009), Многообразия и дифференциальная геометрия, Аспирантура по математике, 107, Провиденс: Американское математическое общество..
- Мичор, Питер В. (2008), Темы по дифференциальной геометрии, Аспирантура по математике, 93, Провиденс: Американское математическое общество..
- Спивак Михаил (1965), Исчисление на многообразиях: современный подход к классическим теоремам продвинутого исчисления, W. A. Benjamin, Inc., ISBN 978-0-8053-9021-6.
внешняя ссылка
- Касательные плоскости в MathWorld

























![{displaystyle {mathrm {d} {varphi} _ {x}} (gamma '(0)) ~ {stackrel {ext {df}} {=}} ~ left. {frac {mathrm {d}} {mathrm {d } {t}}} [(varphi circ gamma) (t)] ight | _ {t = 0},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/802a26bfb082959e820f7e210622c24874c06d79)







![{displaystyle fcirc varphi ^ {- 1}: varphi [U] substeq mathbb {R} ^ {n} o mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8aeb6f9eb7559fb915f3645b06bf2d1da494d814)





































![{displaystyle forall fin {C ^ {infty}} (mathbb {R} ^ {n}): qquad (D_ {v} f) (x) ~ {stackrel {ext {df}} {=}} ~ left. { frac {mathrm {d}} {mathrm {d} {t}}} [f (x + tv)] ight | _ {t = 0} = sum _ {i = 1} ^ {n} v ^ {i} {frac {partial f} {partial x ^ {i}}} (x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c976cc2a64328174c30705c009855435612a50)















![{displaystyle [mathrm {d} {varphi} _ {x} (D)] (f) ~ {stackrel {ext {df}} {=}} ~ D (fcirc varphi).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4287c8ec37c8fd62153b8ab359331810849cc81c)




