Квадратная решетка - Square lattice - Wikipedia

Квадратные решетки
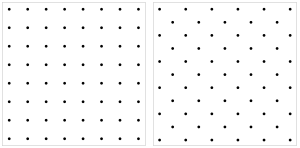Квадратная решетка.svg
Вертикальный квадрат
Простой		диагональный квадрат
По центру
Вертикально квадратная черепица. Вершины всех квадратов вместе со своими центрами образуют прямую квадратную решетку. Для каждого цвета центры квадратов этого цвета образуют диагональную квадратную решетку, которая в линейном масштабе √2 раз больше, чем прямая квадратная решетка.

В математика, то квадратная решетка это тип решетка в двухмерном Евклидово пространство. Это двухмерная версия целочисленная решетка, обозначенный как Z2.[1] Это один из пяти типов двумерных решеток, классифицируемых по их типу. группы симметрии;[2] его группа симметрии в Обозначение IUC в качестве p4m,[3] Обозначение Кокстера как [4,4],[4] и орбифолдная запись как * 442.[5]

Наиболее распространены две ориентации изображения решетки. Их удобно называть вертикальной квадратной решеткой и диагональной квадратной решеткой; последнее также называют центрированная квадратная решетка.[6] Они различаются на угол 45 °. Это связано с тем, что квадратная решетка может быть разбита на две квадратные подрешетки, что видно из раскраски решетки. шахматная доска.

Симметрия

Квадратная решетка симметрия категория группа обоев p4m. Узор с этой решеткой из поступательная симметрия не может иметь больше, но может иметь меньшую симметрию, чем сама решетка. Вертикальную квадратную решетку можно рассматривать как диагональную квадратную решетку с размером ячеек, который в √2 раза больше, с добавленными центрами квадратов. Соответственно, после добавления центров квадратов вертикальной квадратной решетки мы получаем диагональную квадратную решетку с размером ячеек, который в √2 раза меньше, чем у исходной решетки. вращательная симметрия имеет квадратную решетку из 4-кратных ротоцентров, которая в √2 раз тоньше и диагонально ориентирована относительно решетки поступательная симметрия.

Что касается осей отражения, есть три возможности:

  • Никто. Это обои группы p4.
  • По четырем направлениям. Это обои группы p4m.
  • В двух перпендикулярных направлениях. Это группа обоев p4g. Точки пересечения осей отражения образуют квадратную сетку, которая имеет такую ​​же тонкость и ориентирована так же, как квадратная решетка из 4-кратных ротоцентров, причем эти ротоцентры находятся в центрах квадратов, образованных осями отражения.
p4, [4,4]+, (442)p4g, [4,4+], (4*2)p4m, [4,4], (* 442)
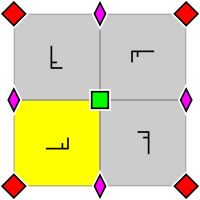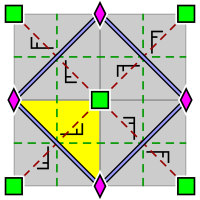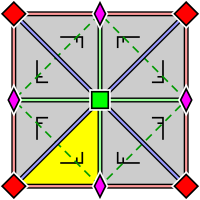Обои групповая диаграмма p4 square.svgГрупповая диаграмма обоев p4g square.svgОбои групповая диаграмма p4m square.svg
Группа обоев p4, с расположением внутри примитивной ячейки 2- и 4-кратных ротоцентров (также применимо для p4g и p4m). Фундаментальный домен обозначен желтым.Группа обоев p4g. Есть оси отражения в двух направлениях, нет через 4-х кратные ротоцентры.Группа обоев p4m. Оси отражения проходят в четырех направлениях через 4-кратные ротоцентры. В двух направлениях оси отражения ориентированы так же, как и для p4g, и с такой же плотностью, но смещены. В двух других направлениях они линейно в √2 раз плотнее.

Смотрите также

Рекомендации

  1. ^ Конвей, Джон; Слоан, Нил Дж. А. (1999), Сферические упаковки, решетки и группы, Springer, стр. 106, ISBN  9780387985855.
  2. ^ Голубицкий, Мартин; Стюарт, Ян (2003), Перспектива симметрии: от равновесия к хаосу в фазовом и физическом пространстве, Успехи в математике, 200, Springer, стр. 129, ISBN  9783764321710.
  3. ^ Филд, Майкл; Голубицкий, Мартин (2009), Симметрия в хаосе: поиск закономерностей в математике, искусстве и природе (2-е изд.), SIAM, стр. 47, ISBN  9780898717709.
  4. ^ Джонсон, Норман В.; Вайс, Азия Ивич (1999), «Целые квадратичные числа и группы Кокстера», Канадский математический журнал, 51 (6): 1307–1336, Дои:10.4153 / CJM-1999-060-6. См., В частности, начало стр. 1320.
  5. ^ Шатчнайдер, Дорис; Сенешаль, Марджори (2004), «Плитки», в Гудман, Джейкоб Э.; О'Рурк, Джозеф (ред.), Справочник по дискретной и вычислительной геометрии, Дискретная математика и ее приложения (2-е изд.), CRC Press, стр. 53–72, ISBN  9781420035315. См., В частности, таблицу на п. 62 связь нотации IUC с нотацией орбифолда.
  6. ^ Johnston, Bernard L .; Ричман, Фред (1997), Числа и симметрия: введение в алгебру, CRC Press, стр. 159, ISBN  9780849303012.