Ширина пути - Pathwidth
В теория графов, а разложение по пути графа грамм неформально является представлением грамм как «загустевший» граф путей,[1] и ширина пути из грамм это число, которое измеряет, насколько утолщен путь, чтобы сформироватьграмм. Более формально, разложение по путям - это последовательность подмножеств вершин грамм такие, что концы каждого ребра входят в одно из подмножеств и каждая вершина входит в непрерывную подпоследовательность подмножеств,[2] и ширина пути на единицу меньше, чем размер самого большого набора в таком разложении. толщина интервала (на один меньше, чем максимальная клика размер в интервал суперграф из грамм), число разделения вершин, или же номер поиска узла.[3]
Пропускная способность и разложение пути во многом аналогичны ширина дерева и разложение деревьев. Они играют ключевую роль в теории граф миноры: семейства графов, замкнутые относительно граф миноры и не включать все леса может быть охарактеризован как имеющий ограниченную ширину пути,[2] и возникающие в общем виде «вихри» структурная теория семейств минорно-замкнутых графов имеют ограниченную пропускную способность.[4] Пропускная способность и графики ограниченной пропускной способности также применяются в СБИС дизайн, рисунок графика, и компьютерная лингвистика.
это NP-жесткий чтобы найти ширину пути произвольных графиков или даже точно ее аппроксимировать.[5][6] Однако проблема в том, управляемый с фиксированными параметрами: проверка, есть ли у графа пропускная способность k может быть решена за время, которое линейно зависит от размера графа, но сверхэкспоненциально отk.[7] Кроме того, для нескольких специальных классов графов, таких как деревья, ширина пути может быть вычислена за полиномиальное время независимо отk.[8][9]Многие проблемы в алгоритмах графов могут быть эффективно решены на графах с ограниченной пропускной способностью, используя динамическое программирование на разбиении по пути графа.[10] Разложение пути также может использоваться для измерения космическая сложность алгоритмов динамического программирования на графах ограниченного ширина дерева.[11]
Определение
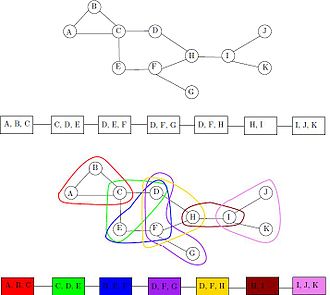
В первой из их знаменитой серии статей о граф миноры, Нил Робертсон и Пол Сеймур (1983 ) определяют разбиение по путям графа грамм быть последовательностью подмножеств Икся вершин грамм, с двумя свойствами:
- Для каждого края грамм, существует я такие, что оба конца ребра принадлежат подмножеству Икся, и
- Для каждых трех индексов я ≤ j ≤ k, Икся ∩ Иксk ⊆ Иксj.
Второе из этих двух свойств эквивалентно требованию, чтобы подмножества, содержащие любую конкретную вершину, образовывали непрерывную подпоследовательность всей последовательности. На языке более поздних работ в малых сериях Робертсона и Сеймура о графах разложение по путям - это разложение дерева (Икс,Т), в котором лежащее в основе дерево Т разложения является граф путей.
Ширина разбиения по путям определяется так же, как и для разбиений по дереву, так как maxя |Икся| - 1, а ширина пути грамм минимальная ширина любого разбиения по путямграмм. Вычитание единицы из размера Икся в этом определении не имеет большого значения для большинства приложений, связанных с пропускной способностью, но используется для определения пропускной способности граф путей быть равным единице.
Альтернативные характеристики
В качестве Бодлендер (1998) описывает, ширину пути можно охарактеризовать многими эквивалентными способами.
Последовательности склеивания
Разложение по пути можно описать как последовательность графов граммя которые склеиваются вместе путем определения пар вершин из последовательных графов в последовательности, так что результат выполнения всех этих склейок равен грамм. Графики граммя можно рассматривать как индуцированные подграфы наборов Икся в первом определении разбиения путей, где две вершины в последовательных индуцированных подграфах склеиваются вместе, когда они индуцируются одной и той же вершиной в грамм, а в обратном направлении можно восстановить множества Икся как множества вершин графов граммя. Тогда ширина разбиения пути на единицу меньше максимального числа вершин в одном из графов. граммя.[2]
Толщина интервала

Пропускная способность любого графа грамм на единицу меньше наименьшего кликового числа интервальный график который содержит грамм как подграф.[13] То есть для каждого разложения пути грамм можно найти интервальный суперграф грамм, и для каждого интервального суперграфа грамм можно найти разложение по пути грамм, такое, что ширина разбиения на единицу меньше кликового числа интервального графа.
В одном направлении, предположим, что разложение по пути грамм дано. Затем можно представить узлы разложения как точки на линии (в порядке пути) и представить каждую вершину v как замкнутый интервал, имеющий эти точки в качестве конечных точек. Таким образом, узлы разложения пути, содержащие v соответствуют репрезентативным точкам в интервале для v. В граф пересечений интервалов, образованных из вершин грамм - интервальный граф, содержащий грамм как подграф. Его максимальные клики задаются наборами интервалов, содержащих репрезентативные точки, а максимальный размер клики равен единице плюс ширина пути грамм.
В обратном направлении, если грамм является подграфом интервального графа с кликовым числом п + 1, тогда грамм имеет разложение по ширине пути п чьи узлы задаются максимальные клики интервального графа. Например, интервальный граф, показанный с его интервальным представлением на рисунке, имеет разбиение по путям с пятью узлами, соответствующими его пяти максимальным кликам. ABC, ACD, CDE, CDF, и FG; максимальный размер клики равен трем, а ширина этого разложения пути равна двум.
Эта эквивалентность между шириной пути и толщиной интервала аналогична эквивалентности между шириной дерева и минимальным кликовым числом (минус один) хордовый граф из которых данный граф является подграфом. Интервальные графы являются частным случаем хордовых графов, а хордовые графы могут быть представлены как графы пересечений поддеревьев общего дерева, обобщая способ, которым интервальные графы являются графами пересечений подпутей пути.
Число разделения вершин
Предположим, что вершины графа грамм находятся линейно упорядоченный. Тогда число разделения вершин грамм это наименьшее число s такое, что для каждой вершины v, в большинстве s вершины раньше, чем v в заказе, но это v или более поздняя вершина в качестве соседа. грамм - минимальное число разделения вершин любого линейного порядка грамм. Число разделения вершин определялось как Эллис, Садборо и Тернер (1983), и равна ширине пути грамм.[14]Это следует из более ранней эквивалентности кликовых чисел интервального графа: если грамм является подграфом интервального графа я, представленного (как на рисунке) таким образом, что все конечные точки интервалов различны, то порядок левых конечных точек интервалов я имеет номер разделения вершин на единицу меньше, чем число кликов я. И наоборот, от линейного упорядочения грамм можно получить представление интервала, в котором левая конечная точка интервала для вершины v это его позиция в порядке, а правая конечная точка - это позиция соседа v который идет последним в заказе.
Номер поиска узла
Игра поиска узла на графе - это форма преследование-уклонение в котором группа поисковиков сотрудничает, чтобы выследить беглеца, скрывающегося на графе. Поисковики размещаются в вершинах графа, в то время как беглец может находиться на любом краю графа, а местонахождение и ходы беглеца скрыты от ищущих. В каждый ход некоторые или все искатели могут перемещаться (произвольно, не обязательно по ребрам) от одной вершины к другой, а затем беглец может двигаться по любому пути в графе, который не проходит через вершину, занятую поисковиком. Беглеца ловят, когда оба конца его края заняты поисковиками. Число поиска узла графа - это минимальное количество искателей, необходимое для гарантированного поимки беглеца, независимо от того, как он двигается. В качестве Кирусис и Пападимитриу (1985) Показано, что количество найденных узлов графа равно его толщине интервала. Оптимальная стратегия для искателей состоит в том, чтобы перемещать искателей таким образом, чтобы в последовательных ходах они образовывали разделяющие множества линейного порядка с минимальным числом разделения вершин.
Границы

Каждый п-вершинный граф с шириной пути k имеет самое большее k(п − k + (k − 1)/2) края, а максимальный ширина путиk Графы (графы, к которым нельзя добавить больше ребер без увеличения ширины пути) имеют ровно столько ребер. Максимальная ширина пути-k график должен быть либо k-путь или k-гусеница, два особых вида k-дерево. А k-дерево - это хордовый граф с точно п − k максимальные клики, каждый из которых содержит k + 1 вершины; в k-дерево, которое само по себе не является (k + 1) -клика, каждая максимальная клика либо разделяет граф на две или более компоненты, либо содержит одну листовую вершину, вершину, которая принадлежит только одной максимальной клике. А k-path - это k-дерево с не более чем двумя листьями и k-гусеница - это k-дерево, которое можно разбить на k-path и набор k-оставляет каждый рядом с разделителем k-клика k-дорожка. В частности, максимальные графики ширины пути - это в точности гусеницы.[15]
Поскольку разложения по путям являются частным случаем разложений по деревьям, ширина пути любого графа больше или равна его ширина дерева. Ширина пути также меньше или равна ширина разреза, минимальное количество ребер, пересекающих любой разрез между вершинами с меньшими и более высокими номерами в оптимальном линейном расположении вершин графа; это следует потому, что число разделения вершин, количество вершин с меньшими номерами и соседями с более высокими номерами, может не более чем равняться количеству отрезанных ребер.[16] По тем же причинам ширина разреза не больше, чем ширина пути, умноженная на максимальная степень вершин данного графа.[17]
Любой п-вертекс лес имеет ширину пути O (журналп).[18] Ведь в лесу всегда можно найти постоянное количество вершин, удаление которых оставляет лес, который можно разделить на два меньших подлеса с не более чем двумяп/ 3 вершины каждая. Линейная структура, образованная рекурсивным разделением каждого из этих двух подлесов с размещением разделяющих вершин между ними, имеет логарифмическое число поиска вершин. Тот же метод, примененный к древовидной декомпозиции графа, показывает, что если ширина дерева п-вершинный граф грамм является т, то ширина пути грамм это O (т бревноп).[19] С внешнепланарные графы, последовательно-параллельные графы, и Графики Халина все имеют ограниченную ширину дерева, все они также имеют логарифмическую ширину пути.
Так же, как и его отношение к ширине дерева, ширина пути также связана с ширина клики и ширина разреза, через линейные графики; линейный график L(грамм) графа грамм имеет вершину для каждого ребра грамм и две вершины в L(грамм) смежны, когда соответствующие два ребра грамм поделиться конечной точкой. Любое семейство графов имеет ограниченную ширину пути тогда и только тогда, когда его линейные графы имеют ограниченную линейную ширину клики, где линейная ширина клики заменяет операцию дизъюнктного объединения из ширины клики на операцию присоединения одной новой вершины.[20] Если связный граф с тремя или более вершинами имеет максимальную степень три, то его ширина сечения равна числу разделенных вершин его линейного графа.[21]
В любом планарный граф, ширина пути не более чем пропорциональна квадратному корню из числа вершин.[22] Один из способов найти разложение по путям с такой шириной - (аналогично логарифмической ширине разложения по путям лесов, описанной выше) использовать теорема о плоском сепараторе найти набор O (√п) вершин, удаление которых разделяет граф на два подграфа не более 2п/ 3 вершины каждая и объединяет рекурсивно построенные разложения путей для каждого из этих двух подграфов. Тот же метод применим к любому классу графов, для которого верна аналогичная теорема о разделителе.[23] Поскольку, как и планарные графы, графы в любом фиксированном семействе минорно-замкнутых графов имеют разделители размера O (√п),[24] отсюда следует, что ширина пути графов в любом фиксированном минорно-замкнутом семействе снова равна O (√п). Для некоторых классов планарных графов ширина пути графа и ширина пути его двойственный граф должны находиться в постоянном множителе друг друга: границы этой формы известны для двусвязных внешнепланарных графов[25] и для многогранных графов.[26] Для двухсвязных плоских графов ширина пути двойного графа меньше, чем ширина пути линейного графа.[27] Остается открытым, всегда ли ширина пути плоского графа и двойственного графа находится в пределах постоянного множителя друг друга в остальных случаях.
В некоторых классах графов было доказано, что ширина пути и ширина дерева всегда равны друг другу: это верно для кографы,[28] графы перестановок,[29] то дополняет из графики сопоставимости,[30] и графики сопоставимости интервальные заказы.[31]
| Нерешенная проблема в математике: Какова максимально возможная ширина пути -вертекс кубический граф ? (больше нерешенных задач по математике) |
В любом кубический граф, или, в более общем смысле, любой граф с максимальной степенью вершины три, ширина пути не более п/ 6 + o (п), куда п - количество вершин в графе. Существуют кубические графы с шириной пути 0,082п, но неизвестно, как уменьшить этот разрыв между этими нижняя граница и п/ 6 верхняя граница.[32]
Вычисление пути-разложения
это НП-полный чтобы определить, не превышает ли ширина пути данного графа k, когда k - переменная, указанная как часть входных данных.[5] Наиболее известные временные границы наихудшего случая для вычисления ширины пути произвольной п-вершинные графы имеют вид O (2п пc) для некоторой постояннойc.[33] Тем не менее, известно несколько алгоритмов для более эффективного вычисления разложения путей, когда ширина пути мала, когда класс входных графов ограничен или приблизительно.
Управляемость с фиксированными параметрами
Ширина пути управляемый с фиксированными параметрами: для любой постоянной k, можно проверить, не превышает ли пропускная способность k, и если да, то найти разложение по пути шириной k, за линейное время.[7] В общем, эти алгоритмы работают в два этапа. На первом этапе предположение, что граф имеет ширину пути k используется, чтобы найти разложение по путям или разложение по дереву, которое не является оптимальным, но ширина которого может быть ограничена как функция k. На втором этапе динамическое программирование Алгоритм применяется к этой декомпозиции, чтобы найти оптимальную декомпозицию, однако временные рамки для известных алгоритмов этого типа экспоненциальны по k2, нецелесообразно, за исключением наименьших значений k.[34] По делу k = 2 явный алгоритм линейного времени, основанный на структурной декомпозиции графов ширины пути-2, имеет вид де Флюитер (1997).
Специальные классы графов
Бодлендер (1994) исследует сложность вычисления ширины пути на различных специальных классах графов. Определение того, является ли ширина пути графа грамм самое большее k остается NP-полным, когда грамм ограничивается графами ограниченной степени,[35] планарные графы,[35] плоские графы ограниченной степени,[35] хордовые графы,[36] хордовые домино,[37] то дополняет из графики сопоставимости,[30]и двудольный дистанционно-наследственные графы.[38] Отсюда сразу следует, что он также является NP-полным для семейств графов, содержащих двудольные графы с дистанционной наследственностью, включая двудольные графы, хордовые двудольные графы, дистанционно наследственные графы и круговые графики.[38]
Однако ширина пути может быть вычислена за линейное время для деревьев и лесов.[9] Это также может быть вычислено за полиномиальное время для графов с ограниченной шириной дерева, включая последовательно-параллельные графы, внешнепланарные графы, и Графики Халина,[7] а также для разделить графики,[39] для дополнений хордовых графов,[40] за графы перестановок,[29] за кографы,[28] за графики дуги окружности,[41] для графиков сопоставимости интервальных порядков,[31] и конечно для интервальные графики сами по себе, поскольку в этом случае ширина пути всего на единицу меньше максимального числа интервалов, покрывающих любую точку в интервальном представлении графа.
Алгоритмы аппроксимации
NP-сложно аппроксимировать ширину пути графа с точностью до аддитивной константы.[6]Самый известный коэффициент аппроксимации алгоритма полиномиального приближения для ширины пути O ((logп)3/2).[42]Для более ранних алгоритмов приближения для ширины пути см. Bodlaender et al. (1992) и Гуха (2000). По поводу приближений на ограниченных классах графов см. Клокс и Бодлендер (1992).
График миноров
А незначительный графа грамм это еще один граф, сформированный из грамм путем сжатия ребер, удаления ребер и удаления вершин. Миноры графов имеют глубокую теорию, в которой несколько важных результатов связаны с шириной пути.
Исключая лес
Если семья F графов закрывается при взятии несовершеннолетних (каждый несовершеннолетний члена F также в F), то по Теорема Робертсона – Сеймура F можно охарактеризовать как графы, не имеющие Икс, куда Икс конечный набор запрещенные несовершеннолетние.[43] Например, Теорема Вагнера заявляет, что планарные графы являются графами, не имеющими полный график K5 ни полный двудольный граф K3,3 как несовершеннолетние. Во многих случаях свойства F и свойства Икс тесно связаны, и первый результат такого рода был сделан Робертсон и Сеймур (1983),[2] и связывает ограниченную ширину пути с существованием лес в семье запрещенных несовершеннолетних. В частности, определите семью F графиков иметь ограниченная ширина пути если существует постоянная п такой, что каждый граф в F имеет пропускную способность не более п. Потом несовершеннолетняя замкнутая семья F имеет ограниченную пропускную способность тогда и только тогда, когда набор Икс запрещенных несовершеннолетних для F включает как минимум один лес.
С одной стороны, этот результат легко доказать: если Икс не включает хотя бы один лес, то Икс-без минорные графы не имеют ограниченной ширины пути. Ведь в этом случае Икс-безопасные графы включают все леса, и в частности, они включают идеальные бинарные деревья. Но идеальное двоичное дерево с 2k +1 уровень имеет пропускную способность k, так что в этом случае Икс-minor-free-графы имеют неограниченную пропускную способность. В обратном направлении, если Икс содержит п-вершинный лес, то Икс-графы без второстепенных имеют пропускную способность не более п − 2.[44]
Препятствия на пути к ограниченной пропускной способности

Свойство иметь максимальную пропускную способность п само закрыто на прием несовершеннолетних: если грамм имеет разложение по пути шириной не более п, то такое же разбиение по путям остается в силе, если из грамм, а любую вершину можно удалить из грамм и от его разложения по траектории без увеличения ширины. Сжатие кромки также может быть выполнено без увеличения ширины разложения путем слияния подпутей, представляющих две конечные точки суженной кромки. Следовательно, графики пропускной способности не более п можно охарактеризовать набором Иксп исключенных несовершеннолетних.[43][45]
Несмотря на то что Иксп обязательно включает в себя хотя бы один лес, неверно, что все графы в Иксп леса: например, Икс1 состоит из двух графов, дерева с семью вершинами и треугольника K3. Однако набор деревьев в Иксп можно точно охарактеризовать: эти деревья - именно те деревья, которые могут быть образованы из трех деревьев в Иксп − 1 путем соединения новой корневой вершины ребром с произвольно выбранной вершиной в каждом из трех меньших деревьев. Например, дерево с семью вершинами в Икс1 формируется таким образом из двухвершинного дерева (одного ребра) в Икс0. Исходя из этой конструкции, количество запрещенных несовершеннолетних в Иксп можно показать как минимум (п!)2.[45] Полный комплект Икс2 вычислено запрещенных миноров для графов с шириной пути-2; он содержит 110 различных графиков.[46]
Теория структуры
В теорема о структуре графа для семейств минорно-замкнутых графов утверждает, что для любого такого семейства F, графики в F можно разложить на кликовые суммы графов, которые могут быть встроенный на поверхности ограниченного род, вместе с ограниченным числом вершин и вихрей для каждой компоненты клик-суммы. Вершина - это вершина, которая может быть смежной с любой другой вершиной в своем компоненте, а вихрь - это граф с ограниченной шириной пути, который приклеен к одной из граней вложения компонента ограниченного рода. Циклическое упорядочение вершин вокруг грани, в которую встроен вихрь, должно быть совместимо с разбиением по траекториям вихря в том смысле, что нарушение цикла для формирования линейного порядка должно приводить к упорядочению с ограниченным числом разделения вершин.[4] Эта теория, в которой ширина пути тесно связана с произвольными семействами минорных замкнутых графов, имеет важные алгоритмические приложения.[47]
Приложения
СБИС
В СБИС При проектировании проблема разделения вершин изначально изучалась как способ разделения схем на более мелкие подсистемы с небольшим количеством компонентов на границе между подсистемами.[35]
Ohtsuki et al. (1979) Используйте толщину интервала для моделирования количества дорожек, необходимых в одномерном макете схемы СБИС, образованной набором модулей, которые необходимо соединить системой цепей. В их модели один формирует граф, в котором вершины представляют сети, и в котором две вершины соединены ребром, если их сети обе соединяются с одним и тем же модулем; то есть, если модули и сети интерпретируются как образующие узлы и гиперребра гиперграф то сформированный из них граф является его линейный график. Интервальное представление суперграфа этого линейного графа вместе с раскраска суперграфа описывает расположение сетей вдоль системы горизонтальных дорожек (по одной дорожке на цвет) таким образом, что модули могут быть размещены вдоль дорожек в линейном порядке и подключены к соответствующим сетям. Тот факт, что интервальные графы идеальные графики[48] подразумевает, что количество необходимых цветов в оптимальном расположении этого типа совпадает с числом кликов интервального завершения сетевого графа.
Схема матрицы ворот[49] это особый стиль CMOS Макет СБИС для Логическая логика схемы. В компоновках матрицы затвора сигналы распространяются вдоль «линий» (сегментов вертикальной линии), в то время как каждый затвор схемы формируется последовательностью характеристик устройства, которые лежат вдоль сегмента горизонтальной линии. Таким образом, сегмент горизонтальной линии для каждого вентиля должен пересекать вертикальные сегменты для каждой из линий, которые формируют входы или выходы элемента. Как и в макетах Ohtsuki et al. (1979), макет этого типа, который минимизирует количество вертикальных дорожек, на которых должны быть расположены линии, может быть найден путем вычисления ширины пути графа, который имеет линии в качестве вершин и пары линий, разделяющих вентиль в качестве ребер.[50] Такой же алгоритмический подход можно использовать для моделирования проблем сворачивания в программируемые логические массивы.[51]
Рисование графика
У Pathwidth есть несколько приложений для рисунок графика:
- Минимальные графы с заданным номер перехода имеют пропускную способность, ограниченную функцией их числа пересечений.[52]
- Количество параллельных линий, на которых вершины дерева могут быть нарисованы без пересечения ребер (при различных естественных ограничениях на способы размещения смежных вершин относительно последовательности линий), пропорционально ширине пути дерева.[53]
- А k-кроссинг час-слойное рисование графика грамм размещение вершин грамм на час четкие горизонтальные линии, края которых проложены как монотонные многоугольные пути между этими линиями таким образом, чтобы k переходы. Графики с такими рисунками имеют ширину пути, ограниченную функцией час и k. Следовательно, когда час и k оба постоянны, можно за линейное время определить, имеет ли граф k-кроссинг час-слойный рисунок.[54]
- График с п вершины и ширина пути п может быть встроен в трехмерную сетку размером п × п × п таким образом, чтобы никакие два ребра (представленные отрезками прямых линий между точками сетки) не пересекались друг с другом. Таким образом, графы с ограниченной шириной пути имеют вложения этого типа с линейным объемом.[55]
Дизайн компилятора
в сборник из языки программирования высокого уровня, ширина пути возникает в задаче переупорядочивания последовательностей прямолинейного кода (то есть кода без поток управления ветвей или циклов) таким образом, чтобы все значения, вычисленные в коде, могли быть помещены в машинные регистры вместо того, чтобы заливать его в основную память. В этом приложении один представляет код, который должен быть скомпилирован, как ориентированный ациклический граф в котором узлы представляют входные значения кода и значения, вычисленные операциями внутри кода. Ребро от узла Икс узел у в этом DAG представляет тот факт, что значение Икс является одним из входов в работу у. А топологический порядок вершин этого DAG представляет собой действительное переупорядочение кода, а количество регистров, необходимых для оценки кода в заданном порядке, задается числом разделения вершин порядка.[56]
На любой фиксированный номер ш машинных регистров, можно определить за линейное время, можно ли переупорядочить фрагмент линейного кода таким образом, чтобы он мог быть оценен не более ш регистры. Действительно, если число разделения вершин топологического упорядочения не превосходит ш, минимальное разделение вершин среди всех порядков не может быть больше, поэтому неориентированный граф, сформированный игнорированием ориентации DAG, описанной выше, должен иметь путь не более ш. Можно проверить, так ли это, используя известные алгоритмы с отслеживанием фиксированных параметров для определения ширины пути, и если да, то найти разложение пути для неориентированного графа за линейное время при условии, что ш является константой.После того, как разложение пути было найдено, топологическое упорядочение ширины ш (если он существует) можно найти с помощью динамического программирования, опять же в линейном времени.[56]
Лингвистика
Корнай и Туза (1992) описать применение ширины пути в обработка естественного языка. В этом приложении предложения моделируются как графы, в которых вершины представляют слова, а ребра представляют отношения между словами; например, если прилагательное изменяет существительное в предложении, тогда граф будет иметь ребро между этими двумя словами. Из-за ограниченных возможностей кратковременной памяти человека,[57] Корнаи и Туза утверждают, что этот граф должен иметь ограниченную ширину пути (точнее, они утверждают, что ширина пути не больше шести), иначе люди не смогут правильно разбирать речь.
Экспоненциальные алгоритмы
Многие проблемы в алгоритмах графов могут быть эффективно решены на графах с низкой пропускной способностью, используя динамическое программирование на разбиении по пути графа.[10] Например, если линейный порядок вершин п-вершинный граф грамм задано, с числом разделения вершин ш, то можно найти максимальный независимый набор грамм во время O (2ш п).[32] На графиках ограниченной ширины пути этот подход приводит к управляемым алгоритмам с фиксированными параметрами, параметризованным шириной пути.[50] Такие результаты не часто встречаются в литературе, потому что они включены в аналогичные алгоритмы, параметризованные шириной дерева; однако ширина пути возникает даже в алгоритмах динамического программирования, основанных на ширине дерева, при измерении космическая сложность этих алгоритмов.[11]
Тот же метод динамического программирования также может быть применен к графам с неограниченной шириной пути, что приводит к алгоритмам, которые решают задачи непараметризованного графа в экспоненциальное время. Например, объединение этого подхода динамического программирования с тем фактом, что кубические графы имеют пропускную способность п/ 6 + o (п) показывает, что в кубическом графе максимальное независимое множество может быть построено за время O (2п/ 6 + o (п)) быстрее, чем предыдущие известные методы.[32] Подобный подход приводит к улучшенным алгоритмам экспоненциального времени для максимальный разрез и минимальный доминирующий набор задачи в кубических графах,[32] и для нескольких других NP-сложных задач оптимизации.[58]
Смотрите также
- Токсичность, другой способ измерения сложности произвольного графа в терминах интервальных графов
- Глубина дерева, число, которое является ограниченным для семейства минорно-замкнутых графов тогда и только тогда, когда семейство исключает путь
- Вырождение, мера разреженности графа, которая не более чем равна ширине его пути
- Пропускная способность графика, другая задача NP-полной оптимизации с использованием линейных схем графов
- Номер Strahler, мера сложности корневых деревьев, определяемая аналогично ширине пути некорневых деревьев
Примечания
- ^ Дистель и Кюн (2005).
- ^ а б c d Робертсон и Сеймур (1983).
- ^ Бодлендер (1998).
- ^ а б Робертсон и Сеймур (2003).
- ^ а б Касивабара и Фудзисава (1979); Ohtsuki et al. (1979); Ленгауэр (1981); Арнборг, Корнейл и Проскуровски (1987).
- ^ а б Bodlaender et al. (1992).
- ^ а б c Бодлендер (1996); Бодлендер и Клокс (1996)
- ^ Бодлендер (1994).
- ^ а б Меринг (1990); Шеффлер (1990); Эллис, Садборо и Тернер (1994); Peng et al. (1998); Скодинис (2000); Скодинис (2003); Кудерт, Хук и Мазурик (2012).
- ^ а б Арнборг (1985).
- ^ а б Аспвалл, Проскуровски и Телле (2000).
- ^ Бодлендер, Ханс Л. (1994). «Путеводитель по деревьям». Acta Cybernetica. 11: 1–2.
- ^ Бодлендер (1998), Теорема 29, с. 13.
- ^ Киннерсли (1992); Бодлендер (1998), Теорема 51.
- ^ Проскуровский и Телле (1999).
- ^ Корах и Солел (1993), Лемма 3 с.99; Бодлендер (1998), Теорема 47, с. 24.
- ^ Корах и Солел (1993), Лемма 1, с. 99; Бодлендер (1998), Теорема 49, с. 24.
- ^ Корах и Солел (1993), Теорема 5, с. 99; Бодлендер (1998), Теорема 66, с. 30. Шеффлер (1992) дает более точную верхнюю границу журнала3(2п + 1) на ширине пути п-верхний лес.
- ^ Корах и Солел (1993), Теорема 6, с. 100; Бодлендер (1998), Следствие 24, стр.10.
- ^ Гурски и Ванке (2007).
- ^ Головач (1993).
- ^ Бодлендер (1998), Следствие 23, с. 10.
- ^ Бодлендер (1998), Теорема 20, с. 9.
- ^ Алон, Сеймур и Томас (1990).
- ^ Бодлендер и Фомин (2002); Кудерт, Хук и Серени (2007).
- ^ Фомин и Тиликос (2007); Амини, Хюк и Перенн (2009).
- ^ Фомин (2003).
- ^ а б Бодлендер и Меринг (1990).
- ^ а б Бодлендер, Клокс и Крач (1993).
- ^ а б Хабиб и Меринг (1994).
- ^ а б Гарбе (1995).
- ^ а б c d Фомин и Хёй (2006).
- ^ Фомин и др. (2008).
- ^ Дауни и товарищи (1999), стр.12.
- ^ а б c d Моньен и Садборо (1988).
- ^ Густедт (1993).
- ^ Клокс, Крач и Мюллер (1995). Хордальное домино - это хордовый граф, в котором каждая вершина принадлежит не более чем двум максимальным кликам.
- ^ а б Kloks et al. (1993).
- ^ Клокс и Бодлендер (1992); Густедт (1993).
- ^ Гарбе (1995) приписывает этот результат доктору философии 1993 г. диссертация Тона Клокса; Алгоритм полиномиального времени Гарбе для графов сравнимости интервальных порядков обобщает этот результат, так как любой хордовый граф должен быть графом сопоставимости этого типа.
- ^ Сучан и Тодинка (2007).
- ^ Файги, Хаджиагайи и Ли (2005).
- ^ а б Робертсон и Сеймур (2004).
- ^ Bienstock et al. (1991); Дистель (1995); Кеттелл, Dinneen & Fellows (1996).
- ^ а б Киннерсли (1992); Такахаши, Уэно и Каджитани (1994); Бодлендер (1998), п. 8.
- ^ Киннерсли и Лэнгстон (1994).
- ^ Демейн, Хаджиагайи и Каварабаяши (2005).
- ^ Берже (1967).
- ^ Лопес и Закон (1980).
- ^ а б Товарищи и Лэнгстон (1989).
- ^ Меринг (1990); Феррейра и песня (1992).
- ^ Глинены (2003).
- ^ Судерман (2004).
- ^ Дуймович и др. (2008).
- ^ Дуймович, Morin & Wood (2003).
- ^ а б Бодлендер, Густедт и Телле (1998).
- ^ Миллер (1956).
- ^ Kneis et al. (2005); Бьёрклунд и Хусфельдт (2008).
Рекомендации
- Алон, Нога; Сеймур, Пол; Томас, Робин (1990), "Теорема о сепараторе для графов с исключенным минором и ее приложения", Proc. 22-й ACM Symp. по теории вычислений (STOC 1990), стр. 293–299, Дои:10.1145/100216.100254, ISBN 0897913612, S2CID 17521329.
- Амини, Омид; Хук, Флориан; Перенн, Стефан (2009), "О ширине пути плоских графов", Журнал SIAM по дискретной математике, 23 (3): 1311–1316, Дои:10.1137/060670146.
- Арнборг, Стефан (1985), "Эффективные алгоритмы для комбинаторных задач на графах с ограниченной разложимостью - обзор", КУСОЧЕК, 25 (1): 2–23, Дои:10.1007 / BF01934985, S2CID 122263659.
- Арнборг, Стефан; Корнейл, Дерек Г.; Проскуровский, Анджей (1987), "Сложность нахождения вложений в k-дерево", Журнал SIAM по алгебраическим и дискретным методам, 8 (2): 277–284, Дои:10.1137/0608024.
- Аспвалл, Бенгт; Проскуровский, Анджей; Телле, Ян Арне (2000), "Требования к памяти для вычислений таблиц в частичных k-дерево алгоритмы ", Алгоритмика, 27 (3): 382–394, Дои:10.1007 / s004530010025, S2CID 9690525.
- Берже, Клод (1967), «Некоторые классы совершенных графов», Теория графов и теоретическая физика, Нью-Йорк: Academic Press, стр. 155–165..
- Бинсток, Дэн; Робертсон, Нил; Сеймур, Пол; Томас, Робин (1991), «Быстро исключая лес», Журнал комбинаторной теории, серия B, 52 (2): 274–283, Дои:10.1016 / 0095-8956 (91) 90068-У.
- Бьёрклунд, Андреас; Хусфельдт, Тор (2008), «Точные алгоритмы для точной выполнимости и количества идеальных соответствий», Алгоритмика, 52 (2): 226–249, Дои:10.1007 / s00453-007-9149-8, S2CID 37693881.
- Бодландер, Ханс Л. (1994), «Путеводитель по деревьям», Дассов, Юрген; Келеменова, Алиса (ред.), Достижения в теоретической информатике (Материалы 7-го Международного собрания молодых ученых-информатиков, Смоленице, 16–20 ноября 1992 г.), Темы компьютерной математики, 6, Гордон и Брич, стр. 1–20..
- Бодландер, Ханс Л. (1996), "Алгоритм линейного времени для поиска разложений дерева малой ширины", SIAM Журнал по вычислениям, 25 (6): 1305–1317, Дои:10.1137 / S0097539793251219, HDL:1874/16670.
- Бодландер, Ханс Л. (1998), "Частичный k-арборетум графов с ограниченной шириной дерева », Теоретическая информатика, 209 (1–2): 1–45, Дои:10.1016 / S0304-3975 (97) 00228-4.
- Бодландер, Ханс Л.; Фомин, Федор В. (2002), "Аппроксимация ширины пути внешнепланарных графов", Журнал алгоритмов, 43 (2): 190–200, Дои:10.1016 / S0196-6774 (02) 00001-9.
- Бодландер, Ханс Л.; Гилберт, Джон Р .; Хафштейнссон, Хьялмтыр; Клокс, Тон (1992), "Приближение ширины дерева, ширины пути и минимальной высоты дерева исключения", Теоретико-графические концепции в компьютерных науках, Конспект лекций по информатике, 570, стр. 1–12, Дои:10.1007/3-540-55121-2_1, HDL:1874/17927, ISBN 978-3-540-55121-8.
- Бодландер, Ханс Л.; Густедт, Йенс; Телле, Ян Арне (1998), "Размещение регистров с линейным временем для фиксированного числа регистров", Proc. 9-й симпозиум ACM – SIAM по дискретным алгоритмам (SODA '98) (PDF), стр. 574–583.
- Бодландер, Ханс Л.; Клокс, Тон (1996), "Эффективные и конструктивные алгоритмы определения ширины пути и ширины дерева графов", Журнал алгоритмов, 21 (2): 358–402, Дои:10.1006 / jagm.1996.0049, HDL:1874/16538.
- Бодландер, Ханс Л.; Клокс, Тон; Kratsch, Дитер (1993), "Ширина дерева и ширина пути графов перестановок", Proc. 20-й Международный коллоквиум по автоматам, языкам и программированию (ICALP 1993), Конспект лекций по информатике, 700, Springer-Verlag, стр. 114–125, Дои:10.1007/3-540-56939-1_66, HDL:1874/16657, ISBN 978-3-540-56939-8.
- Бодландер, Ханс Л.; Меринг, Рольф Х. (1990), "Ширина пути и ширина дерева кографов", Proc. 2-й скандинавский семинар по теории алгоритмов, Конспект лекций по информатике, 447, Springer-Verlag, стр. 301–309, Дои:10.1007/3-540-52846-6_99, HDL:1874/16625, ISBN 978-3-540-52846-3.
- Кеттелл, Кевин; Диннин, Майкл Дж .; Товарищи, Майкл Р. (1996), "Простой алгоритм линейного времени для нахождения разбиений по путям малой ширины", Письма об обработке информации, 57 (4): 197–203, arXiv:математика / 9410211, Дои:10.1016/0020-0190(95)00190-5, S2CID 2442557.
- Кудерт, Дэвид; Хук, Флориан; Мазурик, Дориан (2012), «Распределенный алгоритм для вычисления числа поиска узла в деревьях» (PDF), Алгоритмика, 63 (1): 158–190, Дои:10.1007 / s00453-011-9524-3.
- Кудерт, Дэвид; Хук, Флориан; Серени, Жан-Себастьян (2007), «Ширина пути внешнепланарных графов» (PDF), Журнал теории графов, 55 (1): 27–41, Дои:10.1002 / jgt.20218.
- Дистель, Рейнхард (1995), "Миноры графа I: краткое доказательство теоремы о ширине пути", Комбинаторика, теория вероятностей и вычисления, 4 (1): 27–30, Дои:10.1017 / S0963548300001450.
- Дистель, Рейнхард; Кюн, Даниела (2005), «Граф второстепенных иерархий», Дискретная прикладная математика, 145 (2): 167–182, Дои:10.1016 / j.dam.2004.01.010.
- Демейн, Эрик Д.; Хаджиагайи, Мохаммад Таги; Каварабаяси, Кен-ичи (2005), «Алгоритмическая теория минор графов: декомпозиция, аппроксимация и раскраска», Proc. 46-й симпозиум IEEE по основам компьютерных наук (FOCS 2005), стр. 637–646, Дои:10.1109 / SFCS.2005.14, ISBN 0-7695-2468-0, S2CID 13238254.
- Дауни, Род Г.; Товарищи, Майкл Р. (1999), Параметризованная сложность, Springer-Verlag, ISBN 0-387-94883-X.
- Dujmović, V .; Стипендиаты, M.R.; Китчинг, М .; Liotta, G .; McCartin, C .; Nishimura, N .; Ragde, P .; Розамонд, Ф .; Уайтсайдс, С.; Вуд, Дэвид Р. (2008), «О параметризованной сложности построения многоуровневого графа», Алгоритмика, 52 (2): 267–292, Дои:10.1007 / s00453-007-9151-1, S2CID 2298634.
- Дуймович, Вида; Морен, Пат; Вуд, Дэвид Р. (2003), «Рисунки графиков по ширине и трехмерной прямой сеткой» (PDF), Proc. 10-й Международный симпозиум по графическому рисованию (GD 2002), Конспект лекций по информатике, 2528, Springer-Verlag, стр. 42–53..
- Ellis, J. A .; Sudborough, I.H .; Тернер, Дж. С. (1983), "Разделение графов и поиск числа", Proc. 1983 г., Allerton Conf. по связи, управлению и вычислениям. Как цитирует Моньен и Садборо (1988).
- Ellis, J. A .; Sudborough, I.H .; Тернер, Дж. С. (1994), "Разделение вершин и поисковое число дерева", Информация и вычисления, 113 (1): 50–79, Дои:10.1006 / inco.1994.1064.
- Файги, Уриэль; Хаджиагайи, Мохаммадтаги; Ли, Джеймс Р. (2005), "Улучшенные алгоритмы аппроксимации для разделителей вершин минимального веса", Proc. 37-й симпозиум ACM по теории вычислений (STOC 2005), стр. 563–572, Дои:10.1145/1060590.1060674, ISBN 1581139608, S2CID 14097859.
- Товарищи, Майкл Р.; Лэнгстон, Майкл А. (1989), "О поисковом решении и эффективности полиномиальных алгоритмов", Proc. 21-й симпозиум ACM по теории вычислений, стр. 501–512, Дои:10.1145/73007.73055, ISBN 0897913078, S2CID 1854173.
- Ferreira, Afonso G .; Сонг, Сян В. (1992), «Достижение оптимальности для компоновки матрицы ворот и сворачивания PLA: теоретико-графический подход», Proc. 1-й латиноамериканский симпозиум по теоретической информатике (LATIN '92), Конспект лекций по информатике, 583, Springer-Verlag, стр. 139–153, Дои:10.1007 / BFb0023825, HDL:10068/43314, ISBN 3-540-55284-7.
- де Флюитер, Бабетта (1997), Алгоритмы для графов малой ширины дерева (PDF), Кандидат наук. Тезис, Утрехтский университет, ISBN 90-393-1528-0, заархивировано из оригинал (PDF) на 2011-07-24, получено 2010-05-06.
- Фомин, Федор В. (2003), "Пропускная способность плоских и линейных графов", Графы и комбинаторика, 19 (1): 91–99, Дои:10.1007 / s00373-002-0490-z, S2CID 43123449.
- Фомин, Федор В .; Хойе, Кьяртан (2006), "Пропускная способность кубических графов и точных алгоритмов", Письма об обработке информации, 97 (5): 191–196, Дои:10.1016 / j.ipl.2005.10.012.
- Фомин, Федор В .; Крач, Дитер; Тодинка, Иоан; Виллангер, Ингве (2008), «Точные алгоритмы для ширины дерева и минимального заполнения», SIAM Журнал по вычислениям, 38 (3): 1058–1079, Дои:10.1137/050643350, HDL:1956/1151.
- Фомин, Федор В .; Тиликос, Димитриос М. (2007), "О самодуальности ширины пути в многогранных вложениях графов", Журнал теории графов, 55 (1): 42–54, Дои:10.1002 / jgt.20219.
- Гарбе, Ренате (1995), "Ширина дерева и ширина пути графиков сопоставимости интервальных порядков", Proc. 20-й международный семинар по теоретико-графическим концепциям в компьютерных науках (WG'94), Конспект лекций по информатике, 903, Springer-Verlag, стр. 26–37, Дои:10.1007/3-540-59071-4_35, ISBN 978-3-540-59071-2.
- Головач, П. А. (1993), "Ширина сечения графа и число разделения вершин линейного графа", Дискретная математика и приложения, 3 (5): 517–522, Дои:10.1515 / dma.1993.3.5.517, S2CID 120745961.
- Гуха, Судипто (2000), "Алгоритмы разбиения и аппроксимации вложенных графов", Proc. 41-й симпозиум IEEE по основам компьютерных наук (FOCS 2000), п. 126, Дои:10.1109 / SFCS.2000.892072, ISBN 0-7695-0850-2, S2CID 9854056.
- Гурски, Франк; Ванке, Эгон (2007), "Линейные графы ограниченной ширины клики", Дискретная математика, 307 (22): 2734–2754, Дои:10.1016 / j.disc.2007.01.020.
- Густедт, Йенс (1993), "На пути хордовых графов", Дискретная прикладная математика, 45 (3): 233–248, Дои:10.1016 / 0166-218X (93) 90012-D.
- Хабиб, Мишель; Меринг, Рольф Х. (1994), "Древовидность графов совместимости и новый теоретико-порядковый параметр", Заказ, 11 (1): 47–60, Дои:10.1007 / BF01462229, S2CID 2648030.
- Глинены, Петр (2003), "Критические графы с пересекающимися числами имеют ограниченную ширину пути", Журнал комбинаторной теории, серия B, 88 (2): 347–367, Дои:10.1016 / S0095-8956 (03) 00037-6.
- Кашивабара, Т .; Фудзисава, Т. (1979), "NP-полнота проблемы нахождения графа интервалов с минимальным кликовым числом, содержащего данный граф в качестве подграфа", Proc. Международный симпозиум по схемам и системам, стр. 657–660.
- Киннерсли, Нэнси Г. (1992), "Число разделения вершин графа равно его ширине пути", Письма об обработке информации, 42 (6): 345–350, Дои:10.1016 / 0020-0190 (92) 90234-М.
- Киннерсли, Нэнси Дж .; Лэнгстон, Майкл А. (1994), "Изоляция множества препятствий для задачи компоновки матрицы вентилей", Дискретная прикладная математика, 54 (2–3): 169–213, Дои:10.1016 / 0166-218X (94) 90021-3.
- Kirousis, Lefteris M .; Пападимитриу, Христос Х. (1985), «Интервальные графики и поиск» (PDF), Дискретная математика, 55 (2): 181–184, Дои:10.1016 / 0012-365X (85) 90046-9, заархивировано из оригинал (PDF) на 2011-07-21.
- Клокс, Тон; Бодландер, Ханс Л. (1992), "Аппроксимация ширины дерева и ширины пути некоторых классов совершенных графов", Proc. 3-й Международный симпозиум по алгоритмам и вычислениям (ISAAC'92), Конспект лекций по информатике, 650, Springer-Verlag, стр. 116–125, Дои:10.1007/3-540-56279-6_64, HDL:1874/16672, ISBN 978-3-540-56279-5.
- Клокс, Т .; Бодландер, Х.; Müller, H .; Kratsch, D. (1993), "Вычисление ширины дерева и минимального заполнения: все, что вам нужно, это минимальные разделители", Proc. 1-й Европейский симпозиум по алгоритмам (ESA'93) (конспект лекций по компьютерным наукам), 726, Springer-Verlag, стр. 260–271, Дои:10.1007/3-540-57273-2_61.
- Клокс, Тон; Крач, Дитер; Мюллер, Х. (1995), «Домино», Proc. 20-й международный семинар по теоретико-графическим концепциям в компьютерных науках (WG'94), Конспект лекций по информатике, 903, Springer-Verlag, стр. 106–120, Дои:10.1007/3-540-59071-4_41, ISBN 978-3-540-59071-2.
- Кнейс, Иоахим; Мёлле, Даниэль; Рихтер, Стефан; Россманиф, Питер (2005), "Алгоритмы, основанные на древовидной ширине разреженных графов", Proc. 31-й Международный семинар по теоретико-графическим концепциям в компьютерных науках (WG 2005), Конспект лекций по информатике, 3787, Springer-Verlag, стр. 385–396, Дои:10.1007/11604686_34, ISBN 978-3-540-31000-6.
- Корах, Ефрем; Solel, Nir (1993), «Ширина дерева, ширина пути и ширина разреза», Дискретная прикладная математика, 43 (1): 97–101, Дои:10.1016 / 0166-218X (93) 90171-J.
- Корнаи, Андраш; Tuza, Zsolt (1992), "Узость, ширина пути и их применение в обработке естественного языка", Дискретная прикладная математика, 36 (1): 87–92, Дои:10.1016 / 0166-218X (92) 90208-П.
- Ленгауэр, Томас (1981), «Черно-белые камешки и разделение графиков», Acta Informatica, 16 (4): 465–475, Дои:10.1007 / BF00264496, S2CID 19415148.
- Лопес, Александр Д .; Закон, Хун-Фай С. (1980), "Метод компоновки матрицы с плотным затвором для МОП СБИС", Транзакции IEEE на электронных устройствах, ЭД-27 (8): 1671–1675, Bibcode:1980ITED ... 27.1671L, Дои:10.1109 / T-ED.1980.20086, S2CID 64469353, Также в совместном выпуске, Журнал IEEE по твердотельным схемам 15 (4): 736–740, 1980.
- Миллер, Джордж А. (1956), «Магическое число семь, плюс-минус два», Психологический обзор, 63 (2): 81–97, Дои:10,1037 / ч0043158, PMID 13310704.
- Меринг, Рольф Х. (1990), "Проблемы с графами, связанные с компоновкой матрицы вентилей и сворачиванием PLA", в Tinhofer, G .; Mayr, E .; Noltemeier, H .; и другие. (ред.), Теория вычислительных графов, Computing Supplement, 7, Springer-Verlag, стр. 17–51, ISBN 3-211-82177-5.
- Monien, B .; Садборо, И. Х. (1988), "Min cut NP-полный для деревьев со взвешенными ребрами", Теоретическая информатика, 58 (1–3): 209–229, Дои:10.1016 / 0304-3975 (88) 90028-Х.
- Оцуки, Тацуо; Мори, Хаджиму; Kuh, Ernest S .; Кашивабара, Тошинобу; Fujisawa, Toshio (1979), "Назначение одномерных логических элементов и интервальные графы", Транзакции IEEE в схемах и системах, 26 (9): 675–684, Дои:10.1109 / TCS.1979.1084695.
- Пэн, Шэн-Лунг; Хо, Чин-Вен; Сюй, Цань-шэн; Ко, Мин-Тат; Тан, Чуан И (1998), "Алгоритм линейного времени для построения оптимальной стратегии поиска узлов дерева", Proc. 4-й Int. Конф. Вычислительная техника и комбинаторика (COCOON'98), Конспект лекций по информатике, 1449, Springer-Verlag, стр. 197–205.[мертвая ссылка ].
- Проскуровский, Анджей; Телле, Ян Арне (1999), «Классы графов с ограниченными интервальными моделями» (PDF), Дискретная математика и теоретическая информатика, 3: 167–176, архивировано с оригинал (PDF) на 2011-06-06, получено 2010-05-06.
- Робертсон, Нил; Сеймур, Пол (1983), «График несовершеннолетних. I. Исключая лес», Журнал комбинаторной теории, серия B, 35 (1): 39–61, Дои:10.1016/0095-8956(83)90079-5.
- Робертсон, Нил; Сеймур, Пол (2003), "Миноры графа. XVI. Исключение неплоского графа", Журнал комбинаторной теории, серия B, 89 (1): 43–76, Дои:10.1016 / S0095-8956 (03) 00042-X.
- Робертсон, Нил; Сеймур, Пол Д. (2004), "Миноры графа. XX. Гипотеза Вагнера", Журнал комбинаторной теории, серия B, 92 (2): 325–357, Дои:10.1016 / j.jctb.2004.08.001.
- Шеффлер, Петра (1990), «Линейный алгоритм определения ширины пути деревьев», в Bodendiek, R .; Хенн, Р. (ред.), Темы комбинаторики и теории графов, Physica-Verlag, стр. 613–620..
- Шеффлер, Петра (1992), "Оптимальное вложение дерева в интервальный граф за линейное время", в Нешетржил, Ярослав; Фидлер, Мирослав (ред.), Четвертый чехословацкий симпозиум по комбинаторике, графам и сложности, Эльзевьер.
- Скодинис, Константин (2000), "Вычисление оптимальных линейных макетов деревьев за линейное время", Proc. 8-й Европейский симпозиум по алгоритмам (ESA 2000), Конспект лекций по информатике, 1879, Springer-Verlag, стр. 403–414, Дои:10.1007/3-540-45253-2_37, ISBN 978-3-540-41004-1.
- Скодинис, Константин (2003), "Построение линейных древовидных схем, оптимальных с точки зрения разделения вершин за линейное время", Журнал алгоритмов, 47 (1): 40–59, Дои:10.1016 / S0196-6774 (02) 00225-0.
- Сучан, Кароль; Тодинка, Иоан (2007), "Ширина пути круговых графов", Proc. 33-й международный семинар по теоретико-графическим концепциям в компьютерных науках (WG 2007), Конспект лекций по информатике, 4769, Springer-Verlag, стр. 258–269, Дои:10.1007/978-3-540-74839-7_25.
- Судерман, Мэтью (2004), «Пропускные и многослойные рисунки деревьев» (PDF), Международный журнал вычислительной геометрии и приложений, 14 (3): 203–225, Дои:10.1142 / S0218195904001433, заархивировано из оригинал (PDF) на 2003-05-03.
- Такахаши, Ацуши; Уэно, Шуичи; Каджитани, Йоджи (1994), "Минимальные ациклические запрещенные миноры для семейства графов с ограниченной шириной пути", Дискретная математика, 127 (1–3): 293–304, Дои:10.1016 / 0012-365X (94) 90092-2.

