Линейный график - Line graph
в математический дисциплина теория графов, то линейный график из неориентированный граф г другой граф L (г), который представляет собой смежность между края из г. L (г) строится следующим образом: для каждого ребра в г, сделаем вершину в L (г); на каждые два ребра в г которые имеют общую вершину, сделайте ребро между соответствующими им вершинами в L (г).
Линейный график имени взят из статьи Харари и Норман (1960) хотя оба Уитни (1932) и Крауц (1943) использовал конструкцию до этого.[1] Другие термины, используемые для линейного графика, включают покрывающий граф, то производная, то дуальный от ребра к вершине, то сопрягать, то представительный график, а ϑ-образ,[1] так же хорошо как краевой граф, то график обмена, то присоединенный граф, а производный график.[2]
Хасслер Уитни (1932 ) доказал, что с одним исключительным случаем структура связный граф г можно полностью восстановить из его линейного графика.[3] Многие другие свойства линейных графов следуют путем перевода свойств нижележащего графа из вершин в ребра, и по теореме Уитни такой же перевод может быть выполнен и в другом направлении. Линейные графики без когтей, а линейные графики двудольные графы находятся идеально. Линейные графики характеризуются девятью запрещенные подграфы и может быть признан в линейное время.
Были изучены различные расширения концепции линейного графа, включая линейные графы линейных графов, линейные графы мультиграфов, линейные графики гиперграфов, и линейные графики взвешенных графиков.
Формальное определение
Учитывая график г, его линейный график L(г) - граф такой, что
- каждый вершина из L(г) представляет собой край г; и
- две вершины L(г) находятся смежный тогда и только тогда, когда их соответствующие ребра имеют общую конечную точку («инцидентны») в г.
То есть это граф пересечений краев г, представляющий каждое ребро набором двух его конечных точек.[2]
пример
На следующих рисунках показаны граф (слева, с синими вершинами) и его линейный граф (справа, с зелеными вершинами). Каждая вершина линейного графа помечена парой концов соответствующего ребра исходного графа. Например, зеленая вершина справа, помеченная 1,3, соответствует ребру слева между синими вершинами 1 и 3. Зеленая вершина 1,3 смежна с тремя другими зелеными вершинами: 1,4 и 1,2 (соответствующие к ребрам, разделяющим конечную точку 1 на синем графике) и 4,3 (соответствует ребру, разделяющему конечную точку 3 на синем графике).

График G

Вершины в L (G), построенные из ребер в G

Добавлены ребра в L (G)

Линейный график L (G)
Свойства
Переведенные свойства нижележащего графа
Свойства графа г которые зависят только от смежности между ребрами, могут быть переведены в эквивалентные свойства в L(г), зависящие от смежности вершин. Например, соответствие в г - множество ребер, из которых нет двух смежных, и соответствует набору вершин в L(г) нет двух соседних, т. е. независимый набор.[4]
Таким образом,
- Линейный график связный граф подключен. Если г связан, он содержит дорожка соединяя любые два из его ребер, что переводится в путь в L(г), содержащую любые две вершины L(г). Однако график г который имеет несколько изолированных вершин и поэтому не связан, тем не менее, может иметь связный линейный граф.[5]
- Линейный график имеет точка сочленения тогда и только тогда, когда базовый граф имеет мост для которой ни одна из конечных точек не имеет степени один.[2]
- Для графика г с участием п вершины и м ребра, количество вершин линейного графа L(г) является м, а количество ребер L(г) составляет половину суммы квадратов градусы вершин в г, минус м.[6]
- An независимый набор в L (г) соответствует соответствие в г. В частности, максимальный независимый набор в L (г) соответствует максимальное соответствие в г. Поскольку максимальное сопоставление может быть найдено за полиномиальное время, то же самое можно сделать и с максимальными независимыми наборами линейных графов, несмотря на трудность задачи максимального независимого набора для более общих семейств графов.[4] Аналогично независимый от радуги набор в L(г) соответствует соответствие радуги в г.
- В краевое хроматическое число графа г равно хроматическое число вершины своего линейного графика L(г).[7]
- Линейный график реберно-транзитивный граф является вершинно-транзитивный. Это свойство можно использовать для создания семейств графов, которые (например, Граф Петерсена ) вершинно-транзитивны, но не являются Графики Кэли: если г является реберно-транзитивным графом, который имеет не менее пяти вершин, не является двудольным и имеет нечетные степени вершин, то L(г) - вершинно-транзитивный граф Кэли.[8]
- Если график г имеет Цикл Эйлера, то есть если г связен и имеет четное число ребер в каждой вершине, то линейный граф г является Гамильтониан. Однако не все гамильтоновы циклы в линейных графах происходят из циклов Эйлера таким образом; например, линейный граф гамильтонова графа г сам является гамильтоновым, независимо от того, г также эйлерово.[9]
- Если два простых графика изоморфный тогда их линейные графики также изоморфны. В Теорема об изоморфизме графов Уитни обеспечивает обратное для всех пар графиков, кроме одной.
- В контексте теории сложных сетей линейный граф случайной сети сохраняет многие свойства сети, такие как небольшая собственность (наличие коротких путей между всеми парами вершин) и форма его распределение степеней.[10] Эванс и Ламбьотт (2009) Обратите внимание, что любой метод поиска кластеров вершин в сложной сети можно применить к линейному графу и вместо этого использовать для кластеризации его ребер.
Теорема об изоморфизме Уитни

Если линейные графики двух связанные графы изоморфны, то лежащие в основе графы изоморфны, за исключением случая треугольного графа K3 и коготь K1,3, которые имеют изоморфные линейные графы, но сами не изоморфны.[3]
А также K3 и K1,3, есть некоторые другие исключительные маленькие графы, линейный граф которых имеет более высокую степень симметрии, чем сам граф. Например, ромбовидный график K1,1,2 (два треугольника разделяют ребро) имеет четыре автоморфизмы графов но его линейный график K1,2,2 их восемь. На иллюстрации изображенного ромбовидного графа поворот графа на 90 градусов не является симметрией графа, а симметрией его линейного графа. Однако все такие исключительные случаи имеют не более четырех вершин. Усиленная версия теоремы об изоморфизме Уитни утверждает, что для связных графов с более чем четырьмя вершинами существует взаимно однозначное соответствие между изоморфизмами графов и изоморфизмами их линейных графов.[11]
Аналоги теоремы об изоморфизме Уитни доказаны для линейных графов мультиграфы, но в данном случае они более сложные.[12]
Сильно регулярные и идеальные линейные графики

Линейный график полного графика Kп также известен как треугольный граф, то Граф Джонсона J(п, 2) или дополнять из Граф Кнезера КГп,2. Треугольные графы характеризуются спектры, кроме п = 8.[13] Их также можно охарактеризовать (опять же, за исключением K8) как сильно регулярные графы с параметрами srg (п(п − 1)/2, 2(п − 2), п − 2, 4).[14] Три сильно регулярных графика с теми же параметрами и спектром, что и L(K8) являются Графики Чанга, который может быть получен переключение графиков от L(K8).
Линейный график двудольный граф является идеально (увидеть Теорема Кёнига ), но не обязательно быть двудольным, как показывает пример когтевого графа. Линейные графы двудольных графов образуют один из ключевых строительных блоков совершенных графов, используемых в доказательстве сильная теорема о совершенном графе.[15] Частным случаем этих графов являются графики ладьи, линейные графики полные двудольные графы. Подобно линейным графам полных графов, они могут быть охарактеризованы, за одним исключением, количеством вершин, количеством ребер и количеством общих соседей для смежных и несмежных точек. Единственный исключительный случай: L(K4,4), который имеет общие параметры с Граф Шриханде. Когда обе стороны двумерного разбиения имеют одинаковое количество вершин, эти графы снова становятся сильно регулярными.[16]
В более общем плане график г считается линейный идеальный график если L(г) это идеальный график. Безупречные графы - это именно те графы, которые не содержат простой цикл нечетной длины больше трех.[17] Эквивалентно, график является безупречным тогда и только тогда, когда каждый из его двусвязные компоненты является либо двудольным, либо имеет вид K4 (тетраэдр) или K1,1,п (книга из одного или нескольких треугольников, имеющих общий край).[18] Каждый линейный идеальный график совершенен сам по себе.[19]
Все линейные графики графы без когтей, графики без индуцированный подграф в виде трехлистного дерева.[20] Как и в случае с графами без клешней в целом, каждый связанный линейный граф L(г) с четным числом ребер имеет идеальное соответствие;[21] эквивалентно, это означает, что если базовый граф г имеет четное количество ребер, его ребра можно разбить на двухреберные пути.
Линейные графики деревья точно без когтей блочные графики.[22] Эти графики использовались для решения проблемы в экстремальная теория графов, построения графа с заданным числом ребер и вершин, наибольшее дерево которого индуцированный как подграф как можно меньше.[23]
Все собственные значения из матрица смежности линейного графа не меньше −2. Причина в том, что можно записать как , где - беззнаковая матрица инцидентности предлинейного графа и это личность. Особенно, это Матрица грамиана системы векторов: все графы с этим свойством были названы обобщенными линейными графами.[24]
Характеристика и признание
Раздел клики

Для произвольного графа г, а произвольная вершина v в г, множество ребер, инцидентных v соответствует клика в линейном графике L(г). Образованные таким образом клики разбивают ребра L(г). Каждая вершина L(г) принадлежит ровно двум из них (две клики, соответствующие двум концам соответствующего ребра в г).
Существование такого разбиения на клики можно использовать для характеристики линейных графов: Граф L является линейным графом некоторого другого графа или мультиграфа тогда и только тогда, когда можно найти набор клик в L (позволяя некоторым из клик быть единственными вершинами), которые разделяют ребра L, такая, что каждая вершина L принадлежит ровно двум кликам.[20] Это линейный граф графа (а не мультиграфа), если этот набор клик удовлетворяет дополнительному условию, что никакие две вершины графа L оба находятся в одних и тех же двух кликах. Учитывая такое семейство клик, основной граф г для которого L это линейный граф можно восстановить, сделав одну вершину в г для каждой клики и ребро в г для каждой вершины в L концами которого являются две клики, содержащие вершину в L. По сильной версии теоремы об изоморфизме Уитни, если основной граф г имеет более четырех вершин, может быть только одно разбиение этого типа.
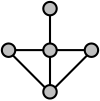
Например, эту характеристику можно использовать, чтобы показать, что следующий график не является линейным графиком:
В этом примере ребра, идущие вверх, влево и вправо от центральной вершины четвертой степени, не имеют общих клик. Следовательно, любое разбиение ребер графа на клики должно иметь по крайней мере одну клику для каждого из этих трех ребер, и все эти три клики будут пересекаться в этой центральной вершине, нарушая требование, чтобы каждая вершина появлялась ровно в двух кликах. Таким образом, показанный график не является линейным.
Запрещенные подграфы

Другая характеристика линейных графиков была доказана в Бейнеке (1970) (и ранее сообщалось без доказательств Бейнеке (1968) ). Он показал, что существует девять минимальных графов, которые не являются линейными, так что любой граф, не являющийся линейным графом, имеет один из этих девяти графов в качестве индуцированный подграф. То есть граф является линейным тогда и только тогда, когда никакое подмножество его вершин не индуцирует один из этих девяти графов. В приведенном выше примере четыре самые верхние вершины образуют коготь (то есть полный двудольный граф K1,3), показанный в верхнем левом углу иллюстрации запрещенных подграфов. Следовательно, согласно характеристике Бейнеке, этот пример не может быть линейным графиком. Для графов с минимальной степенью не ниже 5 для характеристики необходимы только шесть подграфов в левом и правом столбцах рисунка.[25]
Алгоритмы
Руссопулос (1973) и Лехот (1974) описал линейные алгоритмы времени для распознавания линейных графиков и восстановления их исходных графиков. Сысло (1982) обобщил эти методы на ориентированные графы. Дегиорги и Саймон (1995) описал эффективную структуру данных для поддержки динамического графа с учетом вставок и удалений вершин и поддержания представления входных данных в виде линейного графа (если он существует) во времени, пропорциональном количеству измененных ребер на каждом этапе.
Алгоритмы Руссопулос (1973) и Лехот (1974) основаны на характеристиках линейных графов, включающих нечетные треугольники (треугольники в линейном графе с тем свойством, что существует другая вершина, смежная с нечетным числом вершин треугольника). Однако алгоритм Дегиорги и Саймон (1995) использует только теорему об изоморфизме Уитни. Это усложняется необходимостью распознавания удалений, из-за которых оставшийся граф становится линейным графом, но при специализированной задаче статического распознавания необходимо выполнять только вставки, и алгоритм выполняет следующие шаги:
- Построить входной граф L добавляя вершины по одной, на каждом шаге выбирая добавляемую вершину, смежную хотя бы с одной ранее добавленной вершиной. Добавляя вершины к L, вести график г для которого L = L(г); если алгоритм когда-либо не может найти подходящий граф г, то вход не является линейным графиком, и алгоритм завершается.
- При добавлении вершины v к графику L(г) для которого г имеет четыре или меньше вершин, возможно, представление линейного графа не уникально. Но в этом случае расширенный граф достаточно мал, чтобы его представление в виде линейного графа можно было найти с помощью поиск грубой силы в постоянное время.
- При добавлении вершины v к большему графику L что равняется линейному графику другого графика г, позволять S быть подграфом г образованный ребрами, которые соответствуют соседям v в L. Проверь это S имеет крышка вершины состоящий из одной или двух несмежных вершин. Если в крышке две вершины, увеличиваем г добавив ребро (соответствующее v), соединяющий эти две вершины. Если в крышке только одна вершина, то добавить новую вершину в г, примыкающий к этой вершине.
Каждый шаг занимает либо постоянное время, либо включает поиск вершинного покрытия постоянного размера в графе. S размер которого пропорционален количеству соседейv. Таким образом, общее время для всего алгоритма пропорционально сумме чисел соседей всех вершин, которые (по лемма о рукопожатии ) пропорционально количеству входных ребер.
Итерация оператора линейного графика
ван Рой и Вильф (1965) рассмотрим последовательность графов
Они показывают это, когда г конечный связный граф, для этой последовательности возможно только четыре варианта поведения:
- Если г это график цикла тогда L(г) и каждый последующий граф в этой последовательности изоморфный к г сам. Это единственные связные графы, для которых L(г) изоморфна г.[26]
- Если г это коготь K1,3, тогда L(г), а все последующие графы в последовательности - треугольники.
- Если г это граф путей тогда каждый последующий граф в последовательности будет более коротким путем, пока в конечном итоге последовательность не завершится пустой график.
- Во всех остальных случаях размеры графов в этой последовательности со временем неограниченно увеличиваются.
Если г не связан, эта классификация применяется отдельно к каждому компоненту г.
Для связных графов, которые не являются путями, все достаточно большие числа итераций операции линейного графа производят графы, которые являются гамильтоновыми.[27]
Обобщения
Медиальные графы и выпуклые многогранники
Когда планарный граф г имеет максимум степень вершины три, его линейный граф плоский, и каждое плоское вложение г можно продолжить до вложения L(г). Однако существуют плоские графы с более высокой степенью, линейные графы которых неплоские. К ним относятся, например, 5-звездочные K1,5, то драгоценный камень образованный сложением двух непересекающихся диагоналей внутри правильного пятиугольника, и все выпуклые многогранники с вершиной четвертой и более степени.[28]
Альтернативная конструкция, медиальный график, совпадает с линейным графом для плоских графов максимальной степени три, но всегда плоский. У него те же вершины, что и у линейного графа, но потенциально меньше ребер: две вершины медиального графа смежны тогда и только тогда, когда соответствующие два ребра идут подряд на некоторой грани плоского вложения. Медиальный график двойственный граф плоского графа совпадает с медиальным графом исходного плоского графа.[29]
Для правильные многогранники или простых многогранников, операция медиального графа может быть представлена геометрически операцией срезания каждой вершины многогранника плоскостью через середины всех его инцидентных ребер.[30] Эта операция называется вторым усечением,[31] вырожденное усечение,[32] или исправление.[33]
Всего графиков
Общий график Т(г) графа г имеет в качестве вершин элементы (вершины или ребра) г, и имеет край между двумя элементами, когда они инцидентны или смежны. Полный граф можно также получить, разделив каждое ребро г а затем взяв квадрат разделенного графа.[34]
Мультиграфы
Понятие линейного графика г естественным образом распространяется на случай, когда г является мультиграфом. В этом случае характеристики этих графов можно упростить: характеризация в терминах разбиений клик больше не должна предотвращать принадлежность двух вершин к одной и той же клике, а характеристика запрещенными графами имеет семь запрещенных графов вместо девяти.[35]
Однако для мультиграфов существует большее количество пар неизоморфных графов, которые имеют одинаковые линейные графы. Например, полный двудольный граф K1,п имеет тот же линейный график, что и дипольный график и Мультиграф Шеннона с таким же количеством граней. Тем не менее в этом случае аналоги теоремы Уитни об изоморфизме еще можно вывести.[12]
Линейные орграфы

Также возможно обобщить линейные графы на ориентированные графы.[36] Если г ориентированный граф, его ориентированный линейный график или линейный орграф имеет по одной вершине на каждое ребро г. Две вершины, представляющие направленные ребра из ты к v и из ш к Икс в г связаны ребром из УФ к wx в строчном орграфе, когда v = ш. То есть каждое ребро линейного орграфа г представляет собой двунаправленный путь в г. В графы де Брейна может быть сформирован путем повторения этого процесса формирования ориентированных линейных графов, начиная с полный ориентированный граф.[37]
Взвешенные линейные графики
На линейном графике L(г) каждая вершина степени k в исходном графике г создает k(k - 1) / 2 ребра в линейном графе. Для многих типов анализа это означает узлы высокой степени в г чрезмерно представлены на линейном графике L(г). Например, рассмотрим случайная прогулка на вершинах исходного графа г. Это пройдет по краю е с некоторой частотой ж. С другой стороны, этот край е отображается в единственную вершину, скажем v, в линейном графике L(г). Если теперь выполнить такое же случайное блуждание по вершинам линейного графа, частота, с которой v посещаемый может полностью отличаться от ж. Если наш край е в г был связан с узлами степени O (k), он будет пройден O (k2) чаще в линейном графике L(г). Другими словами, теорема об изоморфизме графов Уитни гарантирует, что линейный граф почти всегда кодирует топологию исходного графа. г честно, но это не гарантирует, что динамика на этих двух графиках имеет простую взаимосвязь. Одно из решений - построить взвешенный линейный график, то есть линейный график с взвешенные края. Для этого есть несколько естественных способов.[38] Например, если края d и е в графике г инцидентны в вершине v со степенью k, то на линейном графике L(г) ребро, соединяющее две вершины d и е можно присвоить вес 1 / (k - 1). Таким образом, каждый край в г (при условии, что ни один конец не соединен с вершиной степени 1) будет иметь силу 2 в линейном графе L(г), соответствующие двум концам, которые ребро имеет в г. Это определение взвешенного линейного графа легко распространить на случаи, когда исходный граф г был направлен или даже взвешен.[39] Принцип во всех случаях - обеспечить линейный график L(г) отражает динамику, а также топологию исходного графа г.
Линейные графики гиперграфов
Края гиперграф может образовывать произвольный семейство наборов, так что линейный график гиперграфа такой же, как граф пересечений наборов из семьи.
Граф дизъюнктности
В граф дизъюнктности из г, обозначим D (г), строится следующим образом: для каждого ребра в г, сделаем вершину в D (г); на каждые два ребра в г что делать не имеют общую вершину, сделайте ребро между соответствующими вершинами в D (г).[40] Другими словами, D (г) это дополнительный граф из L (г). А клика в D (г) соответствует независимому множеству в L (г), и наоборот.
Заметки
- ^ а б Хеммингер и Бейнеке (1978), п. 273.
- ^ а б c Харари (1972), п. 71.
- ^ а б Уитни (1932); Крауц (1943); Харари (1972), Теорема 8.3, с. 72. Харари дает упрощенное доказательство этой теоремы следующим образом: Юнг (1966).
- ^ а б Paschos, Vangelis Th. (2010), Комбинаторная оптимизация и теоретическая информатика: интерфейсы и перспективы, John Wiley & Sons, стр. 394, г. ISBN 9780470393673,
Ясно, что существует взаимно однозначное соответствие между сопоставлениями графа и независимыми множествами его линейного графа.
- ^ На необходимость учета изолированных вершин при рассмотрении связности линейных графов указывает Цветкович, Роулинсон и Симич (2004), п. 32.
- ^ Харари (1972), Теорема 8.1, с. 72.
- ^ Дистель, Рейнхард (2006), Теория графов, Тексты для выпускников по математике, 173, Springer, стр. 112, ISBN 9783540261834. Также в бесплатная онлайн-версия, Глава 5 («Раскраски»), с. 118.
- ^ Лаури, Йозеф; Скапеллато, Рафаэле (2003), Темы автоморфизмов и реконструкции графов, Студенческие тексты Лондонского математического общества, 54, Кембридж: Издательство Кембриджского университета, стр. 44, ISBN 0-521-82151-7, Г-Н 1971819. Лаури и Скапеллато приписывают этот результат Марку Уоткинсу.
- ^ Харари (1972), Теорема 8.8, с. 80.
- ^ Рамезанпур, Каримипур и Машаги (2003).
- ^ Юнг (1966); Дегиорги и Саймон (1995).
- ^ а б Зверович (1997)
- ^ ван Дам, Эдвин Р .; Хемерс, Виллем Х. (2003), «Какие графики определяются по их спектру?», Линейная алгебра и ее приложения, 373: 241–272, Дои:10.1016 / S0024-3795 (03) 00483-X, Г-Н 2022290. См., В частности, предложение 8, с. 262.
- ^ Харари (1972), Теорема 8.6, с. 79. Харари приписывает этот результат независимым работам Л. К. Чанга (1959) и А. Дж. Хоффман (1960).
- ^ Чудновский, Мария; Робертсон, Нил; Сеймур, Пол; Томас, Робин (2006), «Сильная теорема о совершенном графе», Анналы математики, 164 (1): 51–229, arXiv:математика / 0212070, Дои:10.4007 / анналы.2006.164.51, S2CID 119151552. Смотрите также Roussel, F .; Rusu, I .; Thuillier, H. (2009), "Сильная гипотеза идеального графа: 40 лет попыток и ее решение", Дискретная математика, 309 (20): 6092–6113, Дои:10.1016 / j.disc.2009.05.024, Г-Н 2552645.
- ^ Харари (1972), Теорема 8.7, с. 79. Харари приписывает эту характеристику линейных графов полных двудольных графов Муну и Хоффману. Случай равного числа вершин на обеих сторонах ранее был доказан Шриханде.
- ^ Троттер (1977); де Верра (1978).
- ^ Маффрей (1992).
- ^ Троттер (1977).
- ^ а б Харари (1972), Теорема 8.4, с. 74, дает три эквивалентные характеристики линейных графов: разбиение ребер на клики, свойство быть без когтей и странно алмаз -свободно и девять запрещенных графов Бейнеке.
- ^ Самнер, Дэвид П. (1974), «Графики с 1-факторами», Труды Американского математического общества, Американское математическое общество, 42 (1): 8–12, Дои:10.2307/2039666, JSTOR 2039666, Г-Н 0323648. Лас Вергнас, М. (1975), «Заметка о сопоставлениях в графах», Cahiers du Centre d'Etudes de Recherche Opérationnelle, 17 (2–3–4): 257–260, Г-Н 0412042.
- ^ Харари (1972), Теорема 8.5, с. 78. Харари приписывает результат Гэри Чартранд.
- ^ Эрдеш, Пол; Сакс, Михаил; Сос, Вера Т. (1986), "Максимально индуцированные деревья в графах", Журнал комбинаторной теории, серия B, 41 (1): 61–79, Дои:10.1016/0095-8956(86)90028-6.
- ^ Цветкович, Роулинсон и Симич (2004).
- ^ Метельский и Тышкевич (1997)
- ^ Этот результат также является теоремой 8.2 из Харари (1972).
- ^ Харари (1972), Теорема 8.11, с. 81. Харари приписывает этот результат Гэри Чартранд.
- ^ Седлачек (1964); Гринвелл и Хеммингер (1972).
- ^ Архидиакон, дан (1992), «Срединный график и дуальность напряжение-ток», Дискретная математика, 104 (2): 111–141, Дои:10.1016 / 0012-365X (92) 90328-D, Г-Н 1172842.
- ^ Макки, Т. А. (1989), "Теоретико-графическая модель географической двойственности", Комбинаторная математика: Труды Третьей Международной конференции (Нью-Йорк, 1985), Анна. New York Acad. Наук, 555, Нью-Йорк: New York Acad. Sci., Стр. 310–315, Bibcode:1989НЯСА.555..310М, Дои:10.1111 / j.1749-6632.1989.tb22465.x, Г-Н 1018637.
- ^ Пью, Энтони (1976), Многогранники: визуальный подход, Калифорнийский университет Press, ISBN 9780520030565.
- ^ Лоеб, Артур Ли (1991), Космические структуры - их гармония и контрапункт (5-е изд.), Birkhäuser, ISBN 9783764335885.
- ^ Вайсштейн, Эрик В. «Ректификация». MathWorld.
- ^ Харари (1972), п. 82.
- ^ Рячек и Врана (2011).
- ^ Харари и Норман (1960).
- ^ Чжан и Линь (1987).
- ^ Эванс и Ламбьотт (2009).
- ^ Эванс и Ламбиотт (2010).
- ^ Мешулам, Рой (01.01.2001). «Кликовый комплекс и соответствие гиперграфа». Комбинаторика. 21 (1): 89–94. Дои:10.1007 / s004930170006. ISSN 1439-6912. S2CID 207006642.
использованная литература
- Beineke, L. W. (1968), "Производные графы орграфов", в Sachs, H .; Voss, H.-J .; Уолтер, Х.-Дж. (ред.), Beiträge zur Graphentheorie, Лейпциг: Teubner, стр. 17–33..
- Бейнеке, Л. В. (1970), "Характеризация производных графов", Журнал комбинаторной теории, 9 (2): 129–135, Дои:10.1016 / S0021-9800 (70) 80019-9, Г-Н 0262097.
- Цветкович, Драгош; Роулинсон, Питер; Симич, Слободан (2004), Спектральные обобщения линейных графиков, Серия лекций Лондонского математического общества, 314, Кембридж: Издательство Кембриджского университета, Дои:10.1017 / CBO9780511751752, ISBN 0-521-83663-8, Г-Н 2120511.
- Degiorgi, Daniele Giorgio; Саймон, Клаус (1995), "Динамический алгоритм распознавания линейных графов", Теоретико-графические концепции в информатике (Аахен, 1995), Конспект лекций по информатике, 1017, Берлин: Springer, стр. 37–48, Дои:10.1007/3-540-60618-1_64, Г-Н 1400011.
- Evans, T.S .; Lambiotte, R. (2009), "Линейные графики, разделы ссылок и перекрывающиеся сообщества", Физический обзор E, 80 (1): 016105, arXiv:0903.2181, Bibcode:2009PhRvE..80a6105E, Дои:10.1103 / PhysRevE.80.016105, PMID 19658772.
- Evans, T.S .; Lambiotte, R. (2010), "Линейные графики взвешенных сетей для перекрывающихся сообществ", Европейский физический журнал B, 77 (2): 265–272, arXiv:0912.4389, Bibcode:2010EPJB ... 77..265E, Дои:10.1140 / epjb / e2010-00261-8, S2CID 119504507.
- Гринвелл, Д. Л .; Хеммингер, Роберт Л. (1972), "Запрещенные подграфы для графов с плоскими линейными графами", Дискретная математика, 2: 31–34, Дои:10.1016 / 0012-365X (72) 90058-1, Г-Н 0297604.
- Харари, Ф.; Норман, Р. З. (1960), "Некоторые свойства линейных орграфов", Rendiconti del Circolo Matematico di Palermo, 9 (2): 161–169, Дои:10.1007 / BF02854581, HDL:10338.dmlcz / 128114, S2CID 122473974.
- Харари, Ф. (1972), «8. Линейные графики», Теория графов (PDF), Massachusetts: Addison-Wesley, pp. 71–83..
- Hemminger, R.L .; Beineke, L. W. (1978), "Линейные графы и линейные орграфы", в Beineke, L.W .; Уилсон, Р. Дж. (Ред.), Избранные темы теории графов, Academic Press Inc., стр. 271–305..
- Юнг, Х.А. (1966), "Zu einem Isomorphiesatz von H. Whitney für Graphen", Mathematische Annalen (на немецком), 164: 270–271, Дои:10.1007 / BF01360250, Г-Н 0197353, S2CID 119898359.
- Краус, Дж. (1943), "Новая демонстрация теории Уитни сюр ле réseaux", Мат. Физ. Лапок, 50: 75–85, Г-Н 0018403.
- Лехот, Филипп Г. Х. (1974), «Оптимальный алгоритм для обнаружения линейного графа и вывода его корневого графа», Журнал ACM, 21 (4): 569–575, Дои:10.1145/321850.321853, Г-Н 0347690, S2CID 15036484.
- Маффре, Фредерик (1992), "Ядра в совершенных линейных графах", Журнал комбинаторной теории, Серия B, 55 (1): 1–8, Дои:10.1016 / 0095-8956 (92) 90028-В, Г-Н 1159851.
- Метельский, Юрий; Тышкевич Регина (1997), "О линейных графах линейных 3-однородных гиперграфов", Журнал теории графов, 25 (4): 243–251, Дои:10.1002 / (SICI) 1097-0118 (199708) 25: 4 <243 :: AID-JGT1> 3.0.CO; 2-K.
- Рамезанпур, А .; Каримипур, В .; Машаги, А. (2003), «Создание коррелированных сетей из некоррелированных», Phys. Ред. E, 67 (4): 046107, arXiv:cond-mat / 0212469, Bibcode:2003PhRvE..67d6107R, Дои:10.1103 / Physreve.67.046107, PMID 12786436, S2CID 33054818.
- van Rooij, A.C.M .; Уилф, Х.С. (1965), «Граф обмена конечного графа», Acta Mathematica Hungarica, 16 (3–4): 263–269, Дои:10.1007 / BF01904834, HDL:10338.dmlcz / 140421, S2CID 122866512.
- Руссопулос, Н. Д. (1973), "Макс {м,п} алгоритм определения графика ЧАС из его линейного графика г", Письма об обработке информации, 2 (4): 108–112, Дои:10.1016 / 0020-0190 (73) 90029-X, Г-Н 0424435.
- Рячек, Зденек; Врана, Петр (2011), "Линейные графы мультиграфов и гамильтонова связность графов без клешней", Журнал теории графов, 66 (2): 152–173, Дои:10.1002 / jgt.20498, Г-Н 2778727.
- Седлачек, J. (1964), "Некоторые свойства обменных графов", Теория графов и ее приложения (Proc. Sympos. Smolenice, 1963)., Publ. Дом Чехословацкой Акад. Sci., Прага, стр. 145–150, Г-Н 0173255.
- Сисло, Мацей М. (1982), "Алгоритм маркировки для распознавания линейного орграфа и вывода его корневого графа", Письма об обработке информации, 15 (1): 28–30, Дои:10.1016/0020-0190(82)90080-1, Г-Н 0678028.
- Троттер, Л. Э. младший (1977), "Линейные совершенные графы", Математическое программирование, 12 (2): 255–259, Дои:10.1007 / BF01593791, Г-Н 0457293, S2CID 38906333.
- де Верра, Д. (1978), "Совершенные графы на линии", Математическое программирование, 15 (2): 236–238, Дои:10.1007 / BF01609025, Г-Н 0509968, S2CID 37062237.
- Уитни, Х. (1932), «Конгруэнтные графы и связность графов», Американский журнал математики, 54 (1): 150–168, Дои:10.2307/2371086, HDL:10338.dmlcz / 101067, JSTOR 2371086.
- Чжан, Фу Цзи; Линь, Го Нин (1987), "О графах де Брейна – Гуда", Acta Math. Синица, 30 (2): 195–205, Г-Н 0891925.
- Зверович, И. Э. (1997), Аналог теоремы Уитни для реберных графов мультиграфов и реберные мультиграфы, Дискретная математика (по-русски), 9 (2): 98–105, Дои:10,4213 / дм478, Г-Н 1468075. Переведено на английский как Зверович, И.. (1997), "Аналог теоремы Уитни для реберных графов мультиграфов и реберных мультиграфов", Дискретная математика и приложения, 7 (3): 287–294, Дои:10.1515 / dma.1997.7.3.287, S2CID 120525090.