Модульность (сети) - Modularity (networks)

Сетевая наука
Теория
График Комплексная сеть Заражение Маленький мир Без накипи Структура сообщества Перколяция Эволюция Управляемость Рисование графика Социальный капитал Анализ ссылок Оптимизация Взаимность Закрытие Гомофилия Транзитивность Предпочтительная привязанность Теория баланса Сетевой эффект Влияние общества
Типы сетей
Информационная (вычислительная) Телекоммуникации Транспорт Социальное Научное сотрудничество Биологические Искусственный нейрон Взаимозависимый Семантический Пространственный Зависимость Поток на чипе
Графики
Функции Клика Компонент Резать Цикл Структура данных Край Петля Район Дорожка Вершина Список смежности  / матрица Список заболеваемости  / матрица Типы Двудольный Полный Режиссер Гипер Мульти Случайный Взвешенный
Метрики Алгоритмы
Центральность Степень Близость Близость PageRank Мотив Кластеризация Распределение степеней Ассортативность Расстояние Модульность Эффективность
Модели
Топология Случайный график Эрдеш – Реньи Барабаши – Альберт Фитнес модель Уоттс-Строгац Экспоненциальный случайный (ERGM) Случайный геометрический (RGG) Гиперболический (HGN) Иерархический Стохастический блок Максимальная энтропия Мягкая конфигурация Тест LFR Динамика Логическая сеть агент на основе Эпидемия /СЭР
Списки Категории
Темы Программного обеспечения Сетевые ученые Категория: Теория сетей Категория: Теория графов

Пример измерения модульности и раскраски на безмасштабная сеть.

Модульность является одним из показателей структуры сети или же графики. Он был разработан для измерения силы разделения сети на модули (также называемые группами, кластерами или сообществами). Сети с высокой модульностью имеют плотные связи между узлами внутри модулей, но редкие связи между узлами в разных модулях. Модульность часто используется в методах оптимизации для обнаружения структура сообщества в сетях. Однако было показано, что модульность страдает пределом разрешения и, следовательно, не может обнаруживать небольшие сообщества. Биологические сети, в том числе мозг животных, обладают высокой степенью модульности.

Мотивация

Многие научно важные проблемы могут быть представлены и эмпирически изучены с помощью сетей. Например, биологические и социальные паттерны, всемирная паутина, метаболические сети, пищевые сети, нейронные сети и патологические сети - это проблемы реального мира, которые можно математически представить и топологически изучить, чтобы выявить некоторые неожиданные структурные особенности.^[1] Большинство этих сетей обладают определенной структурой сообщества, которая имеет существенное значение для понимания динамики сети. Например, тесно связанное социальное сообщество подразумевает более высокую скорость передачи информации или слухов между ними, чем слабо связанное сообщество. Таким образом, если сеть представлена ​​рядом отдельных узлов, соединенных связями, которые обозначают определенную степень взаимодействия между узлами, сообщества определяются как группы плотно связанных узлов, которые лишь редко связаны с остальной частью сети. Следовательно, может быть необходимо идентифицировать сообщества в сетях, поскольку сообщества могут иметь совершенно разные свойства, такие как степень узла, коэффициент кластеризации, промежуточность, центральность.^[2] и т. д., от средней сети. Модульность - одна из таких мер, которая при максимальном увеличении приводит к появлению сообществ в данной сети.

Определение

Модульность - это доля ребер, которые попадают в указанные группы, за вычетом ожидаемой доли, если ребра были распределены случайным образом. Значение модульности для невзвешенных и неориентированных графиков лежит в диапазоне ${displaystyle [-1 / 2,1]}$.^[3] Положительно, если количество ребер в группах превышает число, ожидаемое на основе случайности. Для данного разделения вершин сети на несколько модулей модульность отражает концентрацию ребер внутри модулей по сравнению со случайным распределением связей между всеми узлами независимо от модулей.

Существуют разные методы расчета модульности.^[1] В наиболее распространенной версии концепции рандомизация ребер выполняется так, чтобы сохранить степень каждой вершины. Рассмотрим график с ${displaystyle n}$ узлы и ${displaystyle m}$ ссылки (края ), так что граф можно разделить на два сообщества с помощью переменной принадлежности ${displaystyle s}$. Если узел ${displaystyle v}$ принадлежит к сообществу 1, ${displaystyle s_ {v} = 1}$, или если ${displaystyle v}$ принадлежит к сообществу 2, ${displaystyle s_ {v} = - 1}$. Пусть матрица смежности для сети быть представлен ${displaystyle A}$, куда ${displaystyle A_ {vw} = 0}$ означает, что между узлами нет края (нет взаимодействия) ${displaystyle v}$ и ${displaystyle w}$ и ${displaystyle A_ {vw} = 1}$ означает, что между ними есть грань. Также для простоты мы рассматриваем ненаправленную сеть. Таким образом ${displaystyle A_ {vw} = A_ {wv}}$. (Важно отметить, что между двумя узлами может существовать несколько ребер, но здесь мы рассматриваем простейший случай).

Модульность ${displaystyle Q}$ затем определяется как доля ребер, которые попадают в группу 1 или 2, за вычетом ожидаемого количества ребер в группах 1 и 2 для случайного графа с тем же распределением степеней узлов, что и данная сеть.

Ожидаемое количество ребер должно быть вычислено с использованием концепции модель конфигурации.^[4] Модель конфигурации - это рандомизированная реализация конкретной сети. Учитывая сеть с ${displaystyle n}$ узлы, где каждый узел ${displaystyle v}$ имеет степень узла ${displaystyle k_ {v}}$, модель конфигурации разрезает каждое ребро на две половины, а затем каждую половину ребра, называемую заглушка, случайным образом перенаправляется с любым другим шлейфом в сети (кроме самого себя), даже позволяя петли (которые возникают, когда шлейф перенаправляется на другой шлейф из того же узла) и множественные ребра между теми же двумя узлами. Таким образом, даже если распределение степеней узлов графа остается неизменным, модель конфигурации приводит к полностью случайной сети.

Ожидаемое количество ребер между узлами

Теперь рассмотрим два узла v и ш, с узловыми степенями ${displaystyle k_ {v}}$ и ${displaystyle k_ {w}}$ соответственно, из случайно перепрограммированной сети, как описано выше. Мы вычисляем ожидаемое количество полных ребер между этими узлами.

Пусть общее количество шлейфов в сети будет ${displaystyle l}$:

${displaystyle l = sum _ {u} k_ {u} = 2m}$

(1)

Рассмотрим каждый из ${displaystyle k_ {v}}$ заглушки узла v и создать связанные индикаторные переменные ${displaystyle I_ {i}}$ для них, ${displaystyle i = 1, ldots, k_ {v}}$, с ${displaystyle I_ {i} = 1}$ если i-й шлейф подключается к одному из ${displaystyle k_ {w}}$ заглушки узла ш в этом конкретном случайном графе. Если нет, то его значение равно 0. Поскольку i-я заглушка узла v можно подключиться к любому из ${displaystyle 2m-1}$ оставшиеся заглушки с равной вероятностью, а так как есть ${displaystyle k_ {w}}$ заглушки, к которым он может подключаться, связанные с узлом ш, очевидно

${displaystyle p (I_ {i} = 1) = E [I_ {i}] = {frac {k_ {w}} {2m-1}}}$

Общее количество полных ребер ${displaystyle J_ {vw}}$ между v и ш просто ${displaystyle J_ {vw} = sum _ {i} ^ {k_ {v}} I_ {i}}$, поэтому математическое ожидание этого количества равно

${displaystyle E [J_ {vw}] = E [сумма _ {i} I_ {i}] = сумма _ {i} ^ {k_ {v}} E [I_ {i}] = {frac {k_ {v} k_ {w}} {2m-1}}}$

Затем во многих текстах делаются следующие приближения для случайных сетей с большим количеством ребер. Когда м большой, они отбрасывают вычитание 1 в знаменателе выше и просто используют приближенное выражение ${displaystyle {frac {k_ {v} k_ {w}} {2m}}}$ для ожидаемого количества ребер между двумя узлами. Кроме того, в большой случайной сети количество петель и множественных ребер исчезающе мало.^[5] Игнорирование петель и множественных ребер позволяет предположить, что между любыми двумя узлами имеется не более одного ребра. В таком случае, ${displaystyle J_ {vw}}$ становится двоичной индикаторной переменной, поэтому его ожидаемое значение также является вероятностью того, что оно равно 1, что означает, что можно приблизительно оценить вероятность наличия края между узлами v и ш в качестве ${displaystyle {frac {k_ {v} k_ {w}} {2m}}}$.

Модульность

Следовательно, разница между фактическим количеством ребер между узлами ${displaystyle v}$ и ${displaystyle w}$ и ожидаемое количество ребер между ними равно

${displaystyle A_ {vw} - {frac {k_ {v} k_ {w}} {2m}}}$

Суммирование по всем парам узлов дает уравнение модульности: ${displaystyle Q}$.^[1]

${displaystyle Q = {frac {1} {2m}} sum _ {vw} left [A_ {vw} - {frac {k_ {v} k_ {w}} {2m}} ight] {frac {s_ {v}) s_ {w} +1} {2}}}$

(3)

Важно отметить, что Уравнение 3 годится только для разделения на два сообщества. Иерархическое разделение (то есть разделение на два сообщества, затем два подсообщества далее разделены на два меньших подсообщества только для максимального увеличения Q) - это возможный подход к идентификации нескольких сообществ в сети. Кроме того, (3) может быть обобщено для разделения сети на c сообщества.^[6]

${displaystyle Q = {frac {1} {(2m)}} sum _ {vw} left [A_ {vw} - {frac {k_ {v} k_ {w}} {(2m)}} ight] delta (c_ {v}, c_ {w}) = сумма _ {i = 1} ^ {c} (e_ {ii} -a_ {i} ^ {2})}$

(4)

куда е_ij - доля ребер с односторонними вершинами в сообществе я а другой в сообществе j:

${displaystyle e_ {ij} = sum _ {vw} {frac {A_ {vw}} {2m}} 1_ {vin c_ {i}} 1_ {win c_ {j}}}$

и а_я это доля концов ребер, которые прикреплены к вершинам в сообществе я:

${displaystyle a_ {i} = {frac {k_ {i}} {2m}} = sum _ {j} e_ {ij}}$

Пример обнаружения множественных сообществ

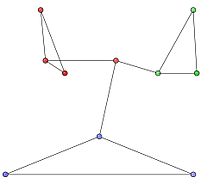
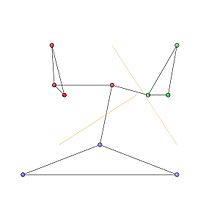
Мы рассматриваем неориентированную сеть с 10 узлами и 12 ребрами и следующей матрицей смежности.

Рис 1. Пример сети, соответствующей матрице смежности с 10 узлами, 12 ребрами.

Рис. 2. Сетевые разделы, увеличивающие Q. Максимальное значение Q = 0,4896.

Сообщества на графике представлены кластерами узлов красного, зеленого и синего цветов на рис. 1. Оптимальные разделы сообщества показаны на рис. 2.

Формулировка матрицы

Альтернативная формулировка модульности, особенно полезная в алгоритмах спектральной оптимизации, выглядит следующим образом.^[1] Определять S_vr быть 1, если вершина v принадлежит к группе р и ноль в противном случае. потом

${displaystyle delta (c_ {v}, c_ {w}) = sum _ {r} S_ {vr} S_ {wr}}$

и поэтому

${displaystyle Q = {frac {1} {2m}} sum _ {vw} sum _ {r} left [A_ {vw} - {frac {k_ {v} k_ {w}} {2m}} ight] S_ { vr} S_ {wr} = {frac {1} {2m}} mathrm {Tr} (mathbf {S} ^ {mathrm {T}} mathbf {BS}),}$

куда S - (неквадратная) матрица, имеющая элементы S_vr и B это так называемая матрица модульности, в которой есть элементы

${displaystyle B_ {vw} = A_ {vw} - {frac {k_ {v} k_ {w}} {2m}}.}$

Сумма всех строк и столбцов матрицы модульности равна нулю, что означает, что модульность неразделенной сети также всегда равна нулю.

Для сетей, разделенных всего на два сообщества, можно альтернативно определить s_v = ± 1, чтобы указать сообщество, которому узел v принадлежит, что затем приводит к

${displaystyle Q = {1 больше 4m} sum _ {vw} B_ {vw} s_ {v} s_ {w} = {1 over 4m} mathbf {s} ^ {mathrm {T}} mathbf {Bs},}$

куда s вектор-столбец с элементами s_v.^[1]

Эта функция имеет тот же вид, что и Гамильтониан Изинга спин-стекло, соединение, которое использовалось для создания простых компьютерных алгоритмов, например, с использованием имитация отжига, чтобы максимизировать модульность. Общая форма модульности для произвольного числа сообществ эквивалентна спин-стеклу Поттса, и аналогичные алгоритмы могут быть разработаны и для этого случая.^[7]

Предел разрешения

Модульность сравнивает количество ребер внутри кластера с ожидаемым количеством ребер, которое можно было бы найти в кластере, если бы сеть была случайной сетью с тем же количеством узлов, и каждый узел сохраняет свою степень, но в противном случае ребра присоединяются случайным образом. Эта случайная нулевая модель неявно предполагает, что каждый узел может быть присоединен к любому другому узлу сети. Это предположение, однако, неразумно, если сеть очень большая, поскольку горизонт узла включает небольшую часть сети, игнорируя большую ее часть. Более того, это означает, что ожидаемое количество ребер между двумя группами узлов уменьшается, если размер сети увеличивается. Итак, если сеть достаточно велика, ожидаемое количество ребер между двумя группами узлов в нулевой модели модульности может быть меньше единицы. Если это произойдет, единственное ребро между двумя кластерами будет интерпретировано модульностью как признак сильной корреляции между двумя кластерами, а оптимизация модульности приведет к слиянию двух кластеров, независимо от характеристик кластеров. Таким образом, даже слабо взаимосвязанные полные графы, которые имеют максимально возможную плотность внутренних ребер и представляют наилучшие идентифицируемые сообщества, были бы объединены путем оптимизации модульности, если бы сеть была достаточно большой.^[8]По этой причине оптимизация модульности в больших сетях не решит проблемы небольших сообществ, даже если они четко определены. Это предубеждение неизбежно для таких методов, как оптимизация модульности, которые полагаются на глобальную нулевую модель.^[9]

Методы с несколькими разрешениями

Есть два основных подхода, которые пытаются решить предел разрешения в контексте модульности: добавление сопротивления р к каждому узлу в виде петля, что увеличивает (г> 0) или уменьшается (г <0) отвращение узлов к формированию сообществ;^[10] или добавление параметра γ> 0 перед термином нулевого регистра в определении модульности, который контролирует относительную важность между внутренними связями сообществ и нулевой моделью.^[7] Оптимизируя модульность для значений этих параметров в соответствующих диапазонах, можно восстановить весь мезомасштаб сети, от макромасштаба, в котором все узлы принадлежат к одному сообществу, до микромасштаба, в котором каждый узел формирует свое собственное сообщество, отсюда и название методы с несколькими разрешениями. Однако было показано, что эти методы имеют ограничения, когда сообщества очень разнородны по размеру.^[11]

Перколяция модульных сетей

Теория перколяции на модульных сетях изучалась несколькими авторами.^[12][13]

Распространение эпидемии в модульных сетях

В последнее время распространение эпидемии было изучено в модульных сетях (сетях с сообществами).^[14]Поскольку распространение болезни в одной стране может стать пандемией с потенциальными гуманитарными и экономическими последствиями во всем мире, важно разработать модели для оценки вероятности всемирной пандемии. Самый свежий пример - коронавирус, который возник в Китае (конец 2019 года) и распространился по всему миру. В этой статье,^[14] предлагается модель распространения болезни в структурной модульной сложной сети (имеющей сообщества) и изучение того, как количество узловых мостов, соединяющих сообщества, влияет на распространение болезни и критерий объявления пандемии.

Смотрите также

• Комплексная сеть
• Структура сообщества
• Нулевая модель
• Теория перколяции

Рекомендации