Проблема с решеткой - Lattice problem

В Информатика, проблемы решетки являются классом оптимизация проблемы, связанные с математическими объектами, называемыми решетки. Предполагаемая неразрешимость таких проблем играет центральную роль в построении безопасных криптосистемы на основе решеток: Проблемы с решеткой являются примером NP-жесткий проблемы, которые, как было показано, являются сложными для среднего случая, обеспечивая тестовый пример безопасности криптографических алгоритмов. Кроме того, некоторые проблемы решетки, которые в худшем случае трудны, могут использоваться в качестве основы для чрезвычайно безопасных криптографических схем. Использование в таких схемах жесткости наихудшего случая делает их одними из очень немногих схем, которые весьма вероятно защищены даже от квантовые компьютеры. Для приложений в таких криптосистемы, решетки над векторное пространство (довольно часто ${displaystyle mathbb {Q} ^ {n}}$) или же бесплатные модули (довольно часто ${displaystyle mathbb {Z} ^ {n}}$) обычно считаются.

Для всех задач ниже предположим, что нам даны (в дополнение к другим более конкретным данным) основа для векторного пространства V и норма N. Обычно рассматриваемая норма - это евклидова норма. L². Однако другие нормы (например, L^п ) также учитываются и отображаются во множестве результатов.^[1] Позволять ${displaystyle lambda (L)}$ обозначим длину кратчайшего ненулевого вектора в решетке L, то есть,

${displaystyle lambda (L) = min _ {vin Lsmallsetminus {mathbf {0}}} | v | _ {N}.}$

Кратчайшая векторная задача (SVP)

Это иллюстрация задачи кратчайшего вектора (базисные векторы синим цветом, кратчайший вектор красным).

В СВП основа из векторное пространство V и норма N (довольно часто L² ) даны для решетки L и нужно найти кратчайший ненулевой вектор в V, как измерено N, в L. Другими словами, алгоритм должен вывести ненулевой вектор v такой, что ${displaystyle N (v) = лямбда (L)}$.

В версии γ-приближения SVP_γ, необходимо найти ненулевой вектор решетки длины не более ${displaystyle gamma cdot lambda (L)}$ для данного ${displaystyle gamma geq 1}$.

Результаты твердости

Точная версия проблемы известна только NP-жесткий для рандомизированных сокращений.^[2][3]

Напротив, соответствующая задача относительно единая норма как известно NP-жесткий. ^[4]

Алгоритмы для евклидовой нормы

Для решения точной версии SVP при евклидовой норме известно несколько различных подходов, которые можно разделить на два класса: алгоритмы, требующие сверхэкспоненциального времени (${displaystyle 2 ^ {omega (n)}}$) и ${displaystyle operatorname {poly} (n)}$ память и алгоритмы, требующие экспоненциального времени и пространства (${displaystyle 2 ^ {Theta (n)}}$) в размерности решетки. Первый класс алгоритмов, в первую очередь, включает решетчатую нумерацию.^[5][6][7] и сокращение случайной выборки^[8][9], в то время как последний включает решетчатое просеивание^[10][11][12], вычисляя ячейку Вороного решетки^[13][14], и дискретная гауссова выборка^[15]. Открытая проблема заключается в том, существуют ли алгоритмы для решения точного SVP, работающие за одно экспоненциальное время (${displaystyle 2 ^ {O (n)}}$) и требуя полиномиального масштабирования памяти в размерности решетки^[16].

Для решения γ-приближения версии SVP_γ за ${displaystyle gamma> 1}$ для евклидовой нормы наиболее известные подходы основаны на использовании редукция базиса решетки. Для больших ${displaystyle gamma = 2 ^ {Omega (n)}}$, то Алгоритм Ленстры – Ленстры – Ловаса (LLL) может найти решение за время, полиномиальное в размерности решетки. Для меньших значений ${displaystyle gamma}$, алгоритм Блока Коркина-Золотарева (БКЗ)^[17][18][19] обычно используется, когда вход в алгоритм (размер блока ${displaystyle eta}$) определяет временную сложность и качество вывода: для больших коэффициентов аппроксимации ${displaystyle gamma}$, небольшой размер блока ${displaystyle eta}$ достаточно, и алгоритм быстро завершается. Для малых ${displaystyle gamma}$, больше ${displaystyle eta}$ необходимы для нахождения достаточно коротких векторов решетки, и алгоритм требует больше времени, чтобы найти решение. Алгоритм BKZ внутренне использует точный алгоритм SVP в качестве подпрограммы (работающий в решетках размерности не более ${displaystyle eta}$), и его общая сложность тесно связана с затратами на эти вызовы SVP в размере ${displaystyle eta}$.

GapSVP

Проблема GapSVP_β состоит в различении экземпляров SVP, в которых длина кратчайшего вектора не превышает ${displaystyle 1}$ или больше чем ${displaystyle eta}$, куда ${displaystyle eta}$ может быть фиксированной функцией размера решетки ${displaystyle n}$. Учитывая основу решетки, алгоритм должен решить, ${displaystyle lambda (L) leq 1}$ или же ${displaystyle lambda (L)> eta}$. Как и другие обещать проблемы, алгоритм может ошибаться во всех остальных случаях.

Еще одна версия проблемы - GapSVP._{ζ, γ} для некоторых функций ${displaystyle zeta, gamma}$. Вход в алгоритм - это основа ${displaystyle B}$ и ряд ${displaystyle d}$. Гарантируется, что все векторы в Ортогонализация Грама – Шмидта имеют длину не менее 1, и что ${displaystyle lambda (L (B)) leq zeta (n)}$ и это ${displaystyle 1leq dleq zeta (n) / gamma (n)}$ куда ${displaystyle n}$ это измерение. Алгоритм должен принять, если ${displaystyle lambda (L (B)) leq d}$, и отклонить, если ${displaystyle lambda (L (B)) geq gamma (n) .d}$. Для больших ${displaystyle zeta}$ (${displaystyle zeta (n)> 2 ^ {n / 2}}$), задача эквивалентна GapSVP_γ потому что^[20] предварительная обработка с использованием LLL алгоритм выполняет второе условие (а значит, ${displaystyle zeta}$) избыточный.

Проблема ближайшего вектора (CVP)

Это иллюстрация ближайшей векторной задачи (базисные векторы - синим, внешний вектор - зеленым, ближайший вектор - красным).

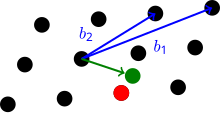
В CVP основа векторного пространства V и метрика M (довольно часто L² ) даны для решетки L, а также вектор v в V но не обязательно в L. Желательно найти вектор в L ближайший к v (измеряется M). в ${displaystyle gamma}$-приближенная версия CVP_γ, необходимо найти вектор решетки на расстоянии не более ${displaystyle gamma}$.

Отношения со старшим вице-президентом

Ближайшая векторная задача - это обобщение самой короткой векторной задачи. Легко показать, что если оракул для CVP_γ (определено ниже), можно решить SVP_γ сделав несколько запросов к оракулу.^[21] Наивный способ найти кратчайший вектор с помощью вызова CVP_γ oracle найти вектор, ближайший к 0, не работает, потому что 0 сам является вектором решетки, и алгоритм потенциально может вывести 0.

Сокращение от СВП_γ в CVP_γ выглядит следующим образом: Предположим, что вход в SVP_γ проблема - основа решетки ${displaystyle B = [b_ {1}, b_ {2}, ldots, b_ {n}]}$. Рассмотрим основу ${displaystyle B ^ {i} = [b_ {1}, ldots, 2b_ {i}, ldots, b_ {n}]}$ и разреши ${displaystyle x_ {i}}$ быть вектором, возвращаемым CVP_γ(B^я, б_я). Утверждается, что кратчайший вектор в наборе ${displaystyle {x_ {i} -b_ {i}}}$ - кратчайший вектор в данной решетке.

Результаты твердости

Goldreich et al. показали, что любая твердость SVP подразумевает такую ​​же твердость для CVP.^[22] С помощью PCP инструменты, Арора и другие. показали, что ЦВД трудно аппроксимировать в пределах фактора ${displaystyle 2 ^ {log ^ {1-epsilon} (n)}}$ пока не ${displaystyle operatorname {NP} subteq operatorname {DTIME} (2 ^ {operatorname {poly} (log n)})}$.^[23] Dinur et al. усилили это, дав результат NP-твердости с ${displaystyle epsilon = (log log n) ^ {c}}$ за ${displaystyle c <1/2}$.^[24]

Расшифровка сферы

Алгоритмы для CVP, особенно вариант Финке и Похста,^[6] использовались для обнаружения данных в множественных входах и множественных выходах (MIMO ) системы беспроводной связи (для кодированных и некодированных сигналов).^[25][13] В этом контексте это называется сферическое декодирование из-за внутреннего радиуса, используемого во многих решениях CVP.^[26]

Он был применен в области разрешения целочисленной неоднозначности несущей GNSS (GPS).^[27] Это называется LAMBDA метод в этой области. В той же области общая проблема CVP упоминается как Целочисленные наименьшие квадраты.

GapCVP

Эта проблема аналогична проблеме GapSVP. Для GapSVP_β, вход состоит из базиса решетки и вектора ${displaystyle v}$ и алгоритм должен ответить, выполняется ли одно из следующих условий:

• существует такой вектор решетки, что расстояние между ним и ${displaystyle v}$ не больше 1.
• каждый вектор решетки находится на расстоянии больше, чем ${displaystyle eta}$ далеко от ${displaystyle v}$.

Противоположное условие - ближайший вектор решетки находится на расстоянии ${displaystyle 1$, отсюда и название ЗазорCVP.

Известные результаты

Проблема тривиально содержится в НП для любого коэффициента приближения.

Шнорр в 1987 году показали, что детерминированные алгоритмы с полиномиальным временем могут решить проблему для ${displaystyle eta = 2 ^ {O (n (log log n) ^ {2} / log n)}}$.^[28] Ajtai et al. показали, что вероятностные алгоритмы могут достичь немного лучшего коэффициента аппроксимации ${displaystyle eta = 2 ^ {O (nlog log n / log n)}}$.^[10]

В 1993 году Банащик показал, что GapCVP_п в ${displaystyle {mathsf {NPcap coNP}}}$.^[29] В 2000 году Гольдрайх и Гольдвассер показали, что ${displaystyle eta = {sqrt {n / log n}}}$ ставит проблему как в NP, так и в коАМ.^[30] В 2005 году Ааронов и Регев показали, что для некоторой постоянной ${displaystyle c}$проблема с ${displaystyle eta = c {sqrt {n}}}$ в ${displaystyle {mathsf {NPcap coNP}}}$.^[31]

Для оценки снизу Dinur et al. показал в 1998 г., что проблема NP-трудна для ${displaystyle eta = n ^ {o (1 / log {log {n}})}}$.^[32]

Задача кратчайших независимых векторов (SIVP)

Для решетки L размерности п, алгоритм должен вывести п линейно независимый ${displaystyle v_ {1}, v_ {2}, ldots, v_ {n}}$ так что ${displaystyle max | v_ {i} | leq max _ {B} | b_ {i} |}$ где правая часть учитывает все основания ${displaystyle B = {b_ {1}, ldots, b_ {n}}}$ решетки.

в ${displaystyle gamma}$-приближенный вариант, заданный решеткой L размерностью п, найти п линейно независимый векторов ${displaystyle v_ {1}, v_ {2}, ldots, v_ {n}}$ длины ${displaystyle max | v_ {i} | leq gamma lambda _ {n} (L)}$, куда ${displaystyle lambda _ {n} (L)}$ это ${displaystyle n}$-й последовательный минимум ${displaystyle L}$.

Декодирование с ограниченным расстоянием

Эта проблема похожа на CVP. Для вектора, удаленного от решетки не более ${displaystyle lambda (L) / 2}$, алгоритм должен вывести ближайший к нему вектор решетки.

Проблема радиуса покрытия

Учитывая основу решетки, алгоритм должен найти наибольшее расстояние (или, в некоторых версиях, его приближение) от любого вектора до решетки.

Кратчайшая проблема базиса

Многие проблемы становятся проще, если исходная база состоит из коротких векторов. Алгоритм, который решает задачу кратчайшего базиса (SBP), должен, учитывая базис решетки ${displaystyle B}$, вывести эквивалентный базис ${displaystyle B '}$ такая, что длина самого длинного вектора в ${displaystyle B '}$ как можно короче.

Приближенный вариант SBP_γ задача состоит в том, чтобы найти базис, самый длинный вектор которого не превышает ${displaystyle gamma}$ раз больше, чем самый длинный вектор в самом коротком базисе.

Использование в криптографии

Средний случай сложность проблем составляет основу доказательств безопасности для большинства криптографических схем. Однако экспериментальные данные свидетельствуют о том, что большинству NP-сложных задач не хватает этого свойства: они, вероятно, только в худшем случае. Были выдвинуты гипотезы или доказано, что многие решеточные задачи являются сложными для среднего случая, что делает их привлекательным классом задач для построения криптографических схем. Более того, для создания безопасных криптографических схем использовалась жесткость наихудшего случая некоторых задач решетки. Использование в таких схемах жесткости наихудшего случая делает их одними из очень немногих схем, которые весьма вероятно защищены даже от квантовые компьютеры.

Приведенные выше решеточные задачи легко решить, если снабдить алгоритм "хорошей" базой. Редукция решетки алгоритмы стремятся, имея основу для решетки, вывести новый базис, состоящий из относительно коротких, почти ортогональный векторов. В Алгоритм редукции решеточного базиса Ленстры – Ленстры – Ловаса (LLL) был ранним эффективным алгоритмом для этой проблемы, который мог выводить почти сокращенный базис решетки за полиномиальное время.^[33] Этот алгоритм и его дальнейшие усовершенствования были использованы для взлома нескольких криптографических схем, что сделало его очень важным инструментом криптоанализа. Успех LLL на экспериментальных данных привел к убеждению, что сокращение решетки может быть простой проблемой на практике. Однако это убеждение было оспорено, когда в конце 1990-х годов было получено несколько новых результатов о сложности решеточных задач, начиная с результата Аджтай.^[2]

В своих основополагающих статьях Аджтай показал, что проблема SVP была NP-сложной, и обнаружил некоторые связи между сложностью наихудшего случая и средняя сложность некоторых решеточных задач.^[2][3] Основываясь на этих результатах, Аджтай и Dwork создал криптосистема с открытым ключом чья безопасность могла быть доказана с использованием только наихудшего случая твердости определенной версии SVP,^[34] Таким образом, это первый результат использования наихудшей жесткости для создания безопасных систем.^[35]

Смотрите также

• Обучение с ошибками
• Краткое целочисленное решение задачи

Рекомендации

дальнейшее чтение

• Agrell, E .; Eriksson, T .; Варди, А .; Зегер, К. (2002). «Поиск ближайшей точки в решетках». IEEE Trans. Инф. Теория. 48 (8): 2201–2214. Дои:10.1109 / TIT.2002.800499.
• Микчанчо, Даниэле (2001). «Задачу кратчайшего вектора {NP} трудно аппроксимировать с точностью до некоторой константы». SIAM Журнал по вычислениям. 30 (6): 2008–2035. CiteSeerX  10.1.1.93.6646. Дои:10.1137 / S0097539700373039.
• Nguyen, Phong Q .; Стерн, Жак (2000). «Сокращение решетки в криптологии: обновление». Материалы 4-го Международного симпозиума по алгоритмической теории чисел. Springer-Verlag. С. 85–112. ISBN  978-3-540-67695-9.