Равносторонний пятиугольник - Equilateral pentagon
Эта статья нужны дополнительные цитаты для проверка. (Август 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В геометрия ан равносторонний пятиугольник это многоугольник с пятью сторонами равной длины. Его пять внутренних углов, в свою очередь, могут принимать ряд наборов значений, что позволяет ему образовывать семейство пятиугольников. Требуется, чтобы все углы в сумме составляли 540 градусов и составляли от 0 до 360 градусов, но не равнялись 180 градусам. Напротив, правильный пятиугольник уникальна, потому что она равносторонняя и к тому же равносторонний (его пять углов равны; мера 108 градусов).
Четырех пересекающихся равных окружностей, образующих замкнутую цепочку, достаточно, чтобы образовался выпуклый равносторонний пятиугольник. Центр каждого круга - одна из четырех вершин пятиугольника. Оставшаяся вершина определяется одной из точек пересечения первой и последней окружностей цепочки.
Пять углов любого выпуклого равностороннего пятиугольника можно описать только двумя углами α и β, при условии, что α ≥ β и δ - наименьший из других углов. Таким образом, общий равносторонний пятиугольник можно рассматривать как двумерную функцию f (α, β) где остальные углы могут быть получены с помощью тригонометрических соотношений. Описанный таким образом равносторонний пятиугольник будет уникальным с точностью до поворота в плоскости.
Примеры
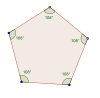 Правильный пятиугольник |  Обычная звезда пентаграмма |  Смежные прямые углы |
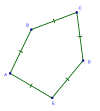 Выпуклый |  Самопересекающийся | 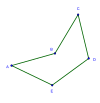 Вогнутый |
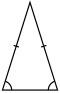 Вырождаются в треугольник (коллинеарные края) |  Вырожденный (перекрытие ребро-вершина) |  Вырождаются в трапецию (коллинеарные края) |
Внутренние углы

Когда равносторонний пятиугольник разрезан на треугольники, два из них выглядят как равнобедренный (треугольники оранжевого и синего цвета), а другой - более общий (треугольник зеленого цвета). Считаем, что нам заданы смежные углы и .
Согласно закон синуса Длина линии, разделяющей зеленый и синий треугольники, составляет:
Квадрат длины линии, разделяющей оранжевый и зеленый треугольники, равен:
Согласно закон косинусов, косинус δ можно увидеть из рисунка:
Упрощая, получаем δ как функцию от α и β:
Остальные углы пятиугольника можно найти геометрически: оставшиеся углы оранжевого и синего треугольников легко найти, заметив, что два угла равнобедренного треугольника равны, а сумма всех трех углов равна 180 °. потом а два оставшихся угла зеленого треугольника можно найти из четырех уравнений, в которых сумма углов пятиугольника равна 540 °, сумма углов зеленого треугольника равна 180 °, угол представляет собой сумму трех его составляющих, а угол представляет собой сумму двух его компонентов.
А циклический пятиугольник равносторонний тогда и только тогда, когда он имеет равные стороны и, следовательно, правильный. Точно так же касательный пятиугольник равносторонний тогда и только тогда, когда он имеет равные углы и, следовательно, правильный.[1]
Двумерное отображение

Равносторонний пятиугольник как функцию двух переменных может быть изображен в двумерном самолет. Каждая пара значений (α, β) отображается в одну точку плоскости, а также в один пятиугольник.
Периодичность значений α и β и условие α ≥ β ≥ δ позволяют ограничить размер отображения. В плоскости с осями координат α и β α = β представляет собой линию, разделяющую плоскость на две части (южная граница показана на чертеже оранжевым цветом). δ = β поскольку кривая делит плоскость на разные части (северная граница показана синим цветом).
Обе границы охватывают непрерывную область плоскости, точки которой соответствуют уникальным равносторонним пятиугольникам. Точки за пределами региона просто соответствуют повторяющимся пятиугольникам, то есть пятиугольникам, которые при повороте или отражении могут совпадать с другими уже описанными. Пентагоны, которые отображаются точно на этих границах, имеют линия симметрии.
Внутри области уникальных отображений есть три типа пятиугольников: звездчатые, вогнутые и выпуклые, разделенные новыми границами.
Звездчатый
В звездчатый стороны пятиугольника пересекаются другими сторонами. Распространенным примером этого типа пятиугольника является пентаграмма. Условие для того, чтобы пятиугольник был звездообразным или самопересекающимся, должен иметь 2α + β ≤ 180 °. Итак, в отображении строка 2α + β = 180 ° (показано оранжевым на севере) - граница между областями звездчатых и не звездчатых пятиугольников. Пентагоны, которые сопоставляются точно с этой границей, имеют вершину, касающуюся другой стороны.
Вогнутый
В вогнутый Пентагоны - это пятиугольники без звездочки, имеющие по крайней мере один угол больше 180 °. Первый угол, который открывается больше 180 °, - это γ, поэтому γ = 180 ° (граница показана зеленым справа) - это кривая, которая является границей областей вогнутых пятиугольников и других, называемых выпуклыми. Пентагоны, которые сопоставляются точно с этой границей, имеют по крайней мере две последовательные стороны, которые выглядят как сторона двойной длины, которая напоминает пятиугольник, вырожденный в четырехугольник.
Выпуклый
В выпуклый Все пять углов пятиугольника меньше 180 °, и никакие стороны не пересекаются с другими. Распространенным примером этого типа пятиугольника является правильный пятиугольник.
Рекомендации
- ^ Де Вильерс, Майкл, "Равносторонние циклические и равносторонние описанные многоугольники", Математический вестник 95, март 2011 г., 102-107.






![{ displaystyle delta = arccos left [ cos ( alpha) + cos ( beta) - cos ( alpha + beta) - { frac {1} {2}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e883c150835971f191c58c20f12c59eb54f44af)


