Упаковка круга - Circle packing

Самый эффективный способ собрать вместе круги разного размера неочевиден.

В геометрия, упаковка круга - это изучение расположения кругов (равных или разных размеров) на заданной поверхности таким образом, чтобы не происходило перекрытия и чтобы ни один круг не мог быть увеличен без создания перекрытия. Связанный плотность упаковки, η, расположения - это доля поверхности, покрытая кругами. Можно сделать обобщения на более высокие измерения - это называется упаковка сфер, который обычно имеет дело только с одинаковыми сферами.

В то время как круг имеет относительно низкую максимальную плотность упаковки 0,9069 на Евклидова плоскость, у него нет самого низкого уровня, даже среди центрально-симметричный выпуклые формы. «Наихудшая» такая форма для установки на самолет еще не определена, но сглаженный восьмиугольник имеет плотность упаковки около 0,902414, что является самой низкой максимальной плотностью упаковки, известной для любой центрально-симметричной выпуклой формы.^[1](Плотность упаковки вогнутых форм, таких как звездные многоугольники может быть сколь угодно малым.)

Раздел математики, обычно известный как «упаковка кругов», занимается геометрией и комбинаторикой упаковки кругов произвольного размера: они порождают дискретные аналоги конформное отображение, Римановы поверхности и тому подобное.

Упаковки в самолете

Одинаковые круги в шестиугольная упаковка расположение, максимально плотная упаковка.

Шестиугольная упаковка за счет естественного расположения равных кругов с переходами к нерегулярному расположению неравных кругов.

В двумерном евклидовом пространстве Жозеф Луи Лагранж в 1773 г. доказал, что решетчатая структура кругов с наибольшей плотностью шестиугольник расположение упаковки,^[2] в котором центры окружностей расположены в шестиугольная решетка (ряды в шахматном порядке, как соты ), и каждый круг окружен 6 другими кругами. Плотность такого расположения для кругов диаметром D, является

${ displaystyle { begin {align} eta _ {h} & ​​= left ({ frac {3 pi} {4}} D ^ {2} div { frac {3 { sqrt {3}) }} {2}} D ^ {2} right) & = { frac { pi { sqrt {3}}} {6}} приблизительно 0,9069. End {align}}}$

D также является стороной шестиугольника на первом рисунке. Первый срок ${ displaystyle { frac {3 pi} {4}} D ^ {2}}$ в приведенном выше соотношении - это сумма площадей всех окружностей и частичных окружностей, заключенных в шестиугольник. Второй срок ${ displaystyle { frac {3 { sqrt {3}}} {2}} D ^ {2}}$ - это площадь самого шестиугольника.

Установлено, что гексагональная упаковка равных кругов заполняет фракцию. ${ displaystyle { frac { pi} { sqrt {12}}} приблизительно 0,9069}$ площади, что было доказано максимальным для периодических упаковок Карл Фридрих Гаусс в 1831 г.^[3] Потом, Аксель Туэ предоставил первое доказательство того, что это было оптимальным в 1890 году, показав, что гексагональная решетка является самой плотной из всех возможных упаковок кругов, как правильных, так и неправильных. Однако некоторые считали его доказательство неполным. Первое строгое доказательство приписывается Ласло Фейес Тот в 1940 г.^[2][4]

С другой стороны, Бёрёчки продемонстрировал, что существуют конфигурации жестко упакованных кругов с произвольно низкой плотностью.^[5][6]

Однородные упаковки

Есть 11 круговых упаковок на основе 11 однородные мозаики самолета.^[7] В этих упаковках каждый круг может быть сопоставлен с любым другим кругом посредством отражений и вращений. В шестиугольник пробелы можно заполнить одним кружком, а двенадцатигранный зазоры можно заполнить 7 кругами, создав 3-однородные упаковки. В усеченная трехгексагональная мозаика с обоими типами зазоров могут быть заполнены как 4-х однородная насадка. В плоская шестиугольная черепица имеет две зеркальные формы.

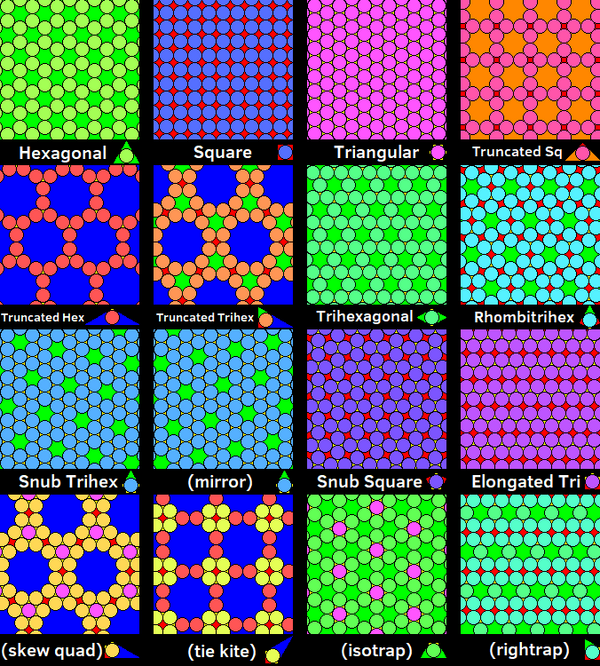
Упаковки на сфере

Связанная с этим проблема состоит в том, чтобы определить расположение идентично взаимодействующих точек с наименьшей энергией, которые должны находиться в пределах заданной поверхности. В Проблема Томсона имеет дело с наименьшим распределением энергии идентичных электрических зарядов на поверхности сферы. В Проблема Таммеса является обобщением этого, имеющим дело с максимизацией минимального расстояния между кругами на сфере. Это аналогично распределению неточечных зарядов на сфере.

Упаковки в ограниченных областях

Пятнадцать равных кругов упакованы в минимально возможную площадь. Всего четыре равносторонних треугольника образованы смежными окружностями.

Упаковочные круги в простых ограниченных формах - распространенный тип проблем в развлекательная математика. Влияние стенок емкости очень важно, а гексагональная упаковка, как правило, не оптимальна для небольшого количества кругов.

Неравные круги

Компактная упаковка бинарных кругов с кругами максимально близкого размера.^[7] Это также наиболее плотная упаковка дисков с таким соотношением размеров (соотношение 0,6375559772 с долей упаковки (удельной площадью) 0,910683).^[8]

Также существует ряд проблем, из-за которых размеры кругов могут быть неоднородными. Одно из таких расширений - найти максимально возможную плотность системы с двумя конкретными размерами круга ( двоичный система). Только девять определенных соотношений радиусов позволяют компактная упаковка, то есть когда каждая пара соприкасающихся кругов находится во взаимном контакте с двумя другими кругами (когда отрезки линии проводятся от соприкасающегося центра круга к центру круга, они триангулируют поверхность).^[7] Для всех этих отношений радиусов известна компактная насадка, которая обеспечивает максимально возможную фракцию упаковки (выше, чем у дисков одинакового размера) для смесей дисков с этим отношением радиусов.^[9] Все девять имеют уплотнения с определенным соотношением, более плотные, чем однородная шестиугольная упаковка, как и некоторые коэффициенты радиуса без компактных уплотнений.^[10]

Также известно, что если отношение радиусов превышает 0,742, бинарная смесь не может уплотняться лучше, чем диски одинакового размера.^[8] Также были получены верхние оценки плотности, которая может быть получена в таких бинарных упаковках при меньших соотношениях.^[11]

Приложения

Квадратурная амплитудная модуляция основан на упаковке кругов в круги внутри фазово-амплитудное пространство. А модем передает данные в виде серии точек в 2-мерной фазо-амплитудной плоскости. Расстояние между точками определяет помехоустойчивость передачи, в то время как диаметр окружности определяет требуемую мощность передатчика. Производительность максимальна, когда созвездие кодовых точек находятся в центрах эффективной упаковки кругов. На практике для упрощения декодирования часто используются субоптимальные прямоугольные упаковки.

Упаковка кругов стала важным инструментом в оригами дизайн, поскольку для каждого придатка фигурки оригами требуется круг из бумаги.^[12] Роберт Дж. Лэнг использовал математику упаковки кругов для разработки компьютерных программ, которые помогают создавать сложные фигурки оригами.

Смотрите также

• Аполлонийская прокладка
• Упаковка круга в квадрат
• Упаковка круга в круг
• Инверсивное расстояние
• Гипотеза Кеплера
• Круги Малфатти
• Проблема с упаковкой

Рекомендации

Библиография

• Уэллс Д. (1991). Словарь любопытной и интересной геометрии Penguin. Нью-Йорк: Книги Пингвинов. стр.30–31, 167. ISBN  0-14-011813-6.
• Стивенсон, Кеннет (декабрь 2003 г.). "Упаковка кругов: математическая сказка" (PDF). Уведомления Американского математического общества. 50 (11).