Топология (электрические схемы) - Topology (electrical circuits)
В топология электронной схемы - это форма, принимаемая сеть взаимосвязей компонентов схемы. Различные конкретные значения или рейтинги компонентов рассматриваются как одна и та же топология. Топология не связана ни с физическим расположением компонентов в схеме, ни с их положением на плате. принципиальная электрическая схема; аналогично математическая концепция топологии, это касается только того, какие связи существуют между компонентами. Может существовать множество физических схем и принципиальных схем, составляющих одну и ту же топологию.
Строго говоря, замена компонента на компонент совершенно другого типа остается той же топологией. Однако в некоторых контекстах их можно условно описать как разные топологии. Например, поменять местами катушки индуктивности и конденсаторы в НЧ фильтр приводит к высокая частота фильтр. Их можно назвать топологиями верхних и нижних частот, даже если топология сети идентична. Более правильный термин для этих классов объектов (т. Е. Сеть, в которой указан тип компонента, но не абсолютное значение): прототип сети.
Топология электронной сети связана с математическая топология, в частности, для сетей, содержащих только двухполюсные устройства, топологию схемы можно рассматривать как применение теория графов. В сетевой анализ такой схемы с топологической точки зрения сеть узлы являются вершины теории графов и ветвей сети являются края теории графов.
Стандартная теория графов может быть расширена для работы с активными компонентами и многополюсными устройствами, такими как интегральные схемы. Графики также могут быть использованы при анализе бесконечные сети.
Принципиальные схемы
В принципиальные схемы в этой статье следуйте обычным соглашениям в электронике;[1] линии представляют собой проводники, закрашенные маленькие кружки представляют соединения проводников, белые маленькие кружки представляют собой клеммы для подключения к внешнему миру. В большинстве случаев импедансы представлены прямоугольниками. На практической принципиальной схеме для обозначения резисторы, индукторы, конденсаторы и т. д., но топология не связана с типом компонента в сети, поэтому символ для общего сопротивление был использован вместо этого.
В Теория графов Раздел этой статьи дает альтернативный метод представления сетей.
Имена топологии
Многие названия топологий связаны с их внешним видом при схематическом изображении. Большинство цепей можно нарисовать разными способами и, следовательно, иметь множество названий. Например, все три схемы, показанные на рисунке 1.1, выглядят по-разному, но имеют идентичную топологию.[2]

Этот пример также демонстрирует общее соглашение об именах топологий после буквы алфавита, с которой они имеют сходство. Таким же образом можно использовать буквы греческого алфавита, например Π (число Пи ) топологии и Δ (дельта ) топология.
Последовательная и параллельная топологии
Для сети с двумя ветвями возможны только две топологии: последовательные и параллельные.

Даже для этих простейших топологий существуют варианты представления схемы.

Для сети с тремя ветвями есть четыре возможных топологии;
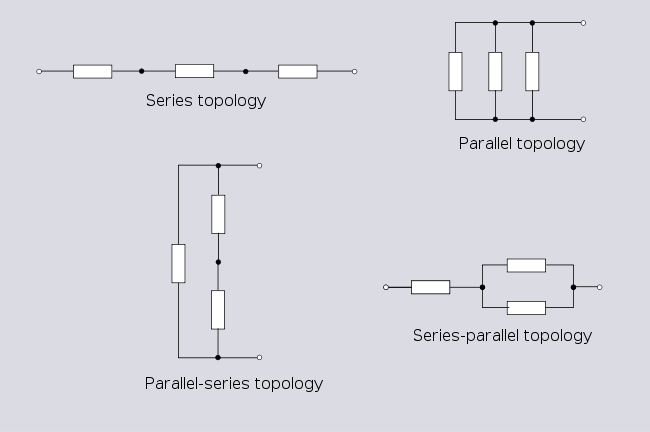
Обратите внимание, что топология параллельных последовательностей - это еще одно представление топологии Delta, обсуждаемое позже.
Последовательные и параллельные топологии можно продолжать создавать с все большим и большим количеством ветвей. до бесконечности. Количество уникальных топологий, которые можно получить из п филиалов 2п-1. Общее количество уникальных топологий, которые могут быть получены не более чем с п филиалов 2п-1.[3]
Y и Δ топологии

Y и Δ являются важными топологиями в линейном сетевом анализе, поскольку они являются простейшими из возможных трехконцевых сетей. А Y-Δ преобразование доступен для линейных цепей. Это преобразование важно, потому что есть некоторые сети, которые нельзя анализировать с точки зрения последовательных и параллельных комбинаций. Эти сети часто возникают в 3-фазных силовых цепях, поскольку они являются двумя наиболее распространенными топологиями для 3-фазных двигателей или обмоток трансформаторов.

Примером этого является сеть на рисунке 1.6, состоящая из сети Y, подключенной параллельно сети Δ. Скажем, нужно рассчитать импеданс между двумя узлами сети. Во многих сетях это можно сделать путем последовательного применения правил комбинации последовательных или параллельных импедансов. Однако это невозможно в этом случае, когда требуется преобразование Y-Δ в дополнение к правилам последовательного и параллельного выполнения.[4]Топология Y также называется звездной топологией. Однако звездообразная топология может также относиться к более общему случаю, когда к одному узлу подключено множество ветвей, а не только три.[5]
Простые топологии фильтров

Топологии, показанные на рисунке 1.7, обычно используются для фильтр и аттенюатор конструкции. Г-образная секция идентична топологии потенциального делителя. Топология тройника идентична топологии Y. Топология section-секции идентична топологии Δ.
Все эти топологии можно рассматривать как короткие разделы лестничная топология. Более длинные участки обычно называют лестничной топологией. Такие схемы обычно анализируются и характеризуются с точки зрения двухпортовая сеть.[6]
Топология моста

Топология моста - важная топология, которая широко используется как в линейных, так и в нелинейных приложениях, включая, среди многих других, мостовой выпрямитель, то Мост Уитстона и фазовый выравниватель на решетке. Есть несколько способов визуализации топологии моста на принципиальных схемах. Первое изображение на рисунке 1.8 является традиционным изображением мостовой схемы. Вторая визуализация ясно показывает эквивалентность между топологией моста и топологией, полученной последовательными и параллельными комбинациями. Третья визуализация более известна как топология решетки. Не так очевидно, что это топологически эквивалентно. Можно увидеть, что это действительно так, визуализируя перемещение верхнего левого узла вправо от верхнего правого узла.

Называть топологию сетевого моста нормально только в том случае, если она используется в качестве двухпортовая сеть со входом и выходом порты каждый состоит из пары диагонально противоположных узлов. Можно увидеть, что блочная топология на рисунке 1.7 идентична топологии моста, но в случае фильтра входные и выходные порты представляют собой пару соседний узлы. Иногда компонент загрузки (или нулевой индикации) на выходном порте моста будет включен в топологию моста, как показано на рисунке 1.9.[7]
Мостовые T- и Twin-T-топологии

Мостовая топология T получена из топологии моста способом, описанным в Сеть Zobel статья. В той же статье также обсуждается множество производных топологий.

Существует также топология Twin-T, которая имеет практическое применение, когда желательно, чтобы вход и выход имели общий (земля ) Терминал. Это может быть, например, потому, что входные и выходные соединения выполнены с коаксиальная топология. Соединение вместе входных и выходных клемм недопустимо при обычной мостовой топологии, и по этой причине Twin-T используется там, где мост в противном случае использовался бы для приложений измерения баланса или нуля. Топология также используется в двойной Т-образный генератор как генератор синусоидальной волны. В нижней части рисунка 1.11 показана перерисованная топология двойного тройника, чтобы подчеркнуть связь с топологией моста.[8]
Бесконечные топологии

Лестничная топология может быть расширен без ограничений и широко используется в конструкциях фильтров. Существует множество вариантов лестничной топологии, некоторые из которых обсуждаются в Топология электронного фильтра и Фильтр составного изображения статьи.
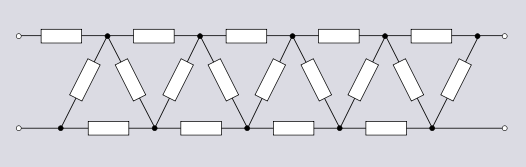
Сбалансированная форма лестничной топологии может рассматриваться как график стороны призма произвольного порядка. Сторона антипризма образует топологию, которая в этом смысле является анти-лестницей. Топология Anti-Ladder находит применение в умножитель напряжения схемы, в частности Генератор Кокрофта-Уолтона. Существует также полноволновая версия генератора Кокрофта-Уолтона, в которой используется двойная анти-лестничная топология.[9]
Бесконечные топологии также могут быть сформированы путем каскадирования нескольких секций какой-либо другой простой топологии, такой как секции решетки или моста-T. Такие бесконечные цепочки секций решетки встречаются при теоретическом анализе и искусственном моделировании линии передачи, но редко используются в качестве практической реализации схемы.[10]
Компоненты с более чем двумя выводами
Цепи, содержащие компоненты с тремя или более терминалами, значительно увеличивают количество возможных топологий. И наоборот, количество различных схем, представленных топологией, уменьшается, и во многих случаях схема легко распознается по топологии, даже если конкретные компоненты не идентифицированы.
 Рисунок 1.14. Базовый усилитель мощности топология, такая как общий эмиттер биполярный переходной транзистор усилитель мощности |  Рисунок 1.15. Симметричный усилитель, такой как длиннохвостая пара усилитель мощности |
Для более сложных схем описание может быть продолжено спецификацией функция передачи между порты сети, а не топологию компонентов.[11]
Теория графов
Теория графов раздел математики, занимающийся графики. В сетевом анализе графики широко используются для представления анализируемой сети. График сети отражает только определенные аспекты сети; те аспекты, которые связаны с его подключением, или, другими словами, с его топологией. Это может быть полезным представлением и обобщением сети, поскольку многие сетевые уравнения инвариантный в сетях с одинаковой топологией. Сюда входят уравнения, полученные из Законы Кирхгофа и Теорема Теллегена.[12]
История
Теория графов использовалась в сетевом анализе линейных пассивных сетей практически с момента формулирования законов Кирхгофа. Густав Кирхгоф Сам в 1847 году использовал графы как абстрактное представление сети в своем анализе петель резистивных цепей.[13] Позднее этот подход был распространен на схемы RLC, заменив сопротивления импедансами. В 1873 г. Джеймс Клерк Максвелл обеспечил двойственность этого анализа с анализом узлов.[14][15] Максвелл также отвечает за топологическую теорему о том, что определитель матрицы узловой проводимости равен сумме всех произведений проводной проводимости дерева. В 1900 г. Анри Пуанкаре представил идею представления графа его матрица инцидентности,[16] отсюда и основание области алгебраическая топология. В 1916 г. Освальд Веблен применил алгебраическую топологию Пуанкаре к анализу Кирхгофа.[17] Веблен также отвечает за внедрение остовное дерево чтобы помочь выбрать совместимый набор сетевых переменных.[18]

Всесторонняя каталогизация сетевых графиков применительно к электрическим цепям началась с Перси МакМахон в 1891 г. (с инженерной статьей в Электрик в 1892 г.), который ограничил свой обзор последовательными и параллельными комбинациями. Мак-Магон назвал эти графы ярмо-цепями.[примечание 1] Рональд М. Фостер в 1932 г. разбили графики на категории по их ничтожность или же классифицировать и предоставил диаграммы всех тех, у кого небольшое количество узлов. Эта работа выросла из более раннего опроса, проведенного Фостером при сотрудничестве с Джордж Кэмпбелл в 1920 г. на 4-портовых телефонных повторителях и произвел 83539 различных графиков.[19]
Долгое время топология в теории электрических цепей касалась только линейных пассивных сетей. Более поздние разработки полупроводниковых устройств и схем потребовали новых инструментов в топологии для их работы. Огромное увеличение сложности схемы привело к использованию комбинаторика в теории графов для повышения эффективности компьютерных вычислений.[18]
Графики и принципиальные схемы

Сети обычно классифицируются по типу электрические элементы придумывая их. На принципиальной схеме эти типы элементов специально нарисованы, каждый со своим уникальным символом. Резистивные сети представляют собой одноэлементные сети, состоящие только из р элементы. Аналогичным образом, емкостные или индуктивные сети являются одноэлементными. В RC, RL и LC схемы представляют собой простые двухэлементные сети. В RLC схема простейшая трехэлементная сеть. В LC лестничная сеть, обычно используемая для фильтры нижних частот может иметь много элементов, но это еще один пример двухэлементной сети.[20]
И наоборот, топология касается только геометрических отношений между элементами сети, а не самих элементов. В основе топологического представления сети лежит график сети. Элементы представлены как края графа. Край рисуется в виде линии, заканчивающейся точками или маленькими кружками, из которых могут исходить другие края (элементы). В схемотехническом анализе ребра графа называются ветви. Точки называются вершины графика и представляют узлы сети. Узел и вершина - это термины, которые могут использоваться как синонимы при обсуждении графов сетей. На рис. 2.2 показано графическое представление схемы на рис. 2.1.[21]
Графики, используемые в сетевом анализе, обычно, кроме того, ориентированные графы, чтобы зафиксировать направление тока и напряжения, и помеченные графики, чтобы уловить уникальность ветвей и узлов. Например, граф, состоящий из квадрата ветвей, останется тем же топологическим графом, если две ветви поменять местами, если только ветви не будут однозначно помечены. В ориентированных графах два узла, к которым подключается ветвь, обозначаются как исходный и целевой узлы. Обычно они обозначаются стрелкой, нарисованной на ветке.[22]
Заболеваемость
Частота - одно из основных свойств графика. Ребро, соединенное с вершиной, называется инцидент на этой вершине. Случайность графика может быть зафиксирована в матричном формате с помощью матрицы, называемой матрицей инцидентности. Фактически, матрица инцидентности - это альтернативное математическое представление графика, которое не требует каких-либо рисунков. Строки матрицы соответствуют узлам, а столбцы матрицы соответствуют ветвям. Элементы матрицы либо равны нулю, если нет инцидентности, либо единице, если инцидент между узлом и ветвью. Направление в ориентированных графах обозначается знаком элемента.[18][23]
Эквивалентность
Графы эквивалентны, если один можно преобразовать в другой путем деформации. Деформация может включать в себя операции перевод, вращение и отражение; сгибание и вытягивание веток; и скрещивание или завязывание ветвей. Два графа, эквивалентные по деформации, называются конгруэнтный.[24]
В области электрических сетей есть два дополнительных преобразования, которые, как считается, приводят к эквивалентным графам, которые не дают конгруэнтных графов. Первый из них - это чередование последовательно соединенных ветвей. Это двойная замена параллельно соединенных ветвей, которая может быть достигнута путем деформации без применения специального правила. Второй касается графиков, разделенных на два или более отдельные части, то есть граф с двумя наборами узлов, у которых нет ветвей, относящихся к узлу в каждом наборе. Две такие отдельные части считаются графом, эквивалентным одному, в котором части соединяются путем объединения узла из каждой в один узел. Аналогичным образом, граф, который можно разделить на две отдельные части, разделив узел пополам, также считается эквивалентным.[25]
Деревья и ссылки

А дерево представляет собой граф, в котором все узлы прямо или косвенно связаны ветвями, но без образования замкнутых циклов. Поскольку замкнутых контуров нет, в дереве нет токов. В сетевом анализе нас интересуют остовные деревья, то есть деревья, которые соединяют каждый узел, присутствующий в графе сети. В этой статье под остовным деревом понимается неквалифицированный дерево если не указано иное. Данный сетевой граф может содержать несколько разных деревьев. Ветви, удаленные из графа, чтобы сформировать дерево, называются ссылки, оставшиеся в дереве ветви называются веточки. Для графика с п узлов, количество ветвей в каждом дереве, т, должно быть;
Важное соотношение для анализа цепей:
куда б - количество ветвей в графе и ℓ - количество ссылок, удаленных для формирования дерева.[26]
Наборы галстуков и кройки
Целью анализа цепей является определение всех токов и напряжений ответвлений в сети. Не все эти сетевые переменные независимы. Напряжения ответвления связаны с токами ответвления функция передачи элементов, из которых они состоят. Таким образом, полное решение сети может быть выражено только в отношении токов ответвления или напряжений ответвления. И не все токи ответвления независимы друг от друга. Минимальное количество токов ответвления, необходимое для полного решения, составляет л. Это следствие того, что дерево имеет л ссылки удалены и в дереве не может быть токов. Поскольку остальные ветви дерева имеют нулевой ток, они не могут быть независимыми от токов звена. Токи ветвей, выбранные как набор независимых переменных, должны быть набором, связанным со звеньями дерева: нельзя выбрать никакие л ветки произвольно.[27]
Что касается напряжений ответвлений, полное решение сети может быть получено с т напряжения на ответвлении. Это следствие того факта, что короткое замыкание всех ветвей дерева приводит к тому, что напряжение везде равно нулю. Следовательно, напряжения звена не могут быть независимыми от напряжений ветвей дерева.[28]

Обычный подход к анализу заключается в поиске петлевые токи а не токи ответвления. Затем токи ответвления находятся в терминах токов контура. Опять же, набор петлевых токов не может быть выбран произвольно. Чтобы гарантировать набор независимых переменных, токи контура должны быть связаны с определенным набором контуров. Этот набор циклов состоит из этих циклов, образованных заменой одного звена данного дерева графа анализируемой схемы. Поскольку при замене одного звена в дереве образуется ровно одна уникальная петля, определенное таким образом количество петлевых токов равно л. Период, термин петля в этом контексте это не то же самое, что обычное значение петля в теории графов. Набор ветвей, образующих данный цикл, называется набор галстуков.[заметка 2] Набор сетевых уравнений формируется путем приравнивания токов контура к алгебраической сумме токов ветвления связующего набора.[29]
Можно выбрать набор независимых токов контура без привязки к деревьям и связкам. Достаточным, но не необходимым условием для выбора набора независимых циклов является обеспечение того, чтобы каждый выбранный цикл включал хотя бы одну ветвь, которая ранее не была включена в уже выбранные циклы. Особенно простой выбор используется в анализ сетки в котором все петли выбраны в качестве сеток.[заметка 3] Сеточный анализ может применяться только в том случае, если можно отобразить график на плоскости или сфере без пересечения ветвей. Такие графы называются планарные графы. Возможность отображения на плоскость или сферу - эквивалентные условия. Любой конечный граф, отображаемый на плоскость, можно сжать до тех пор, пока он не отобразится на небольшой области сферы. И наоборот, сетка любого графа, отображаемого на сферу, может быть растянута до тех пор, пока пространство внутри нее не займет почти всю сферу. В этом случае весь граф занимает лишь небольшую часть сферы. Это то же самое, что и в первом случае, поэтому график также будет отображаться на плоскости.[30]
Существует подход к выбору сетевых переменных с аналогичными напряжениями и двойной к методу токовой петли. Здесь напряжение, связанное с парами узлов, является первичными переменными, и напряжения ответвлений находятся в их терминах. В этом методе также необходимо выбрать конкретное дерево графа, чтобы гарантировать, что все переменные независимы. Двойной набор галстуков является вырезать набор. Набор связей формируется тем, что все связи графа, кроме одной, могут быть разомкнутыми. Набор для резки формируется путем короткого замыкания всех ветвей, кроме одной. Набор сокращений состоит из ветви дерева, которая не была замкнута накоротко, и любых звеньев, которые не были замкнуты накоротко другими ветвями дерева. Разрезанный набор графа дает два непересекающихся подграфы, то есть он разрезает граф на две части и представляет собой минимальный набор ветвей, необходимых для этого. Набор сетевых уравнений формируется путем приравнивания напряжений пары узлов к алгебраической сумме напряжений ветвей вырезанного набора.[31] Двойственным частным случаем анализа сеток является узловой анализ.[32]
Аннулирование и ранг
Ничтожность, N, графа с s отдельные части и б ветви определяется;
Нулевое значение графа представляет собой количество степеней свободы его набора сетевых уравнений. Для плоского графа нулевое значение равно количеству ячеек в графе.[33]
Звание, р графа определяется;
Ранг играет ту же роль в узловом анализе, что и нулевое значение в анализе сетки. То есть он дает количество требуемых уравнений узлового напряжения. Ранг и ничтожность - понятия двойственные и связаны между собой:[34]
Решение сетевых переменных
После выбора набора геометрически независимых переменных состояние сети выражается через них. В результате получается набор независимых линейных уравнений, которые необходимо решено одновременно чтобы найти значения сетевых переменных. Этот набор уравнений может быть выражен в матричном формате, который приводит к характеристической матрице параметров для сети. Матрицы параметров имеют вид матрица импеданса если уравнения были сформированы на основе анализа петель, или как матрица проводимости если уравнения составлены на основе узлового анализа.[35]
Эти уравнения можно решить несколькими хорошо известными способами. Один из методов - это систематическое исключение переменных.[36] Другой метод предполагает использование детерминанты. Это известно как Правило Крамера и обеспечивает прямое выражение неизвестной переменной в терминах определителей. Это полезно тем, что дает компактное выражение для решения. Однако для чего-то большего, чем самые простые сети, этот метод требует больших вычислительных усилий при работе вручную.[37]
Двойственность
Два графа являются двойственными, если отношения между ветвями и парами узлов в одном такие же, как отношения между ветвями и циклами в другом. Двойник графа может быть полностью найден графический метод.[38]
Двойник графа - это другой граф. Для данного дерева в графе дополнительный набор ветвей (т. Е. Ветвей не в дереве) формирует дерево в двойственном графе. Набор уравнений токовой петли, связанный с наборами связей исходного графа и дерева, идентичен набору уравнений пары узлов напряжения, связанных с наборами разрезов двойного графа.[39]
В следующей таблице перечислены двойственные концепции топологии, связанные с теорией схем.[40]

| Текущий | Напряжение |
| Дерево | Лабиринт |
| Ответвляться | Ответвляться |
| Сетка | Узел |
| Петля | Пара узлов |
| Связь | Ветвь дерева |
| Набор галстуков | Вырезать набор |
| Короткое замыкание | Разомкнутая цепь |
| Параллельное соединение | Последовательное соединение |
| Недействительность | Классифицировать |
Дуал дерева иногда называют лабиринт[примечание 4] Оно состоит из пространств, соединенных ссылками так же, как дерево состоит из узлов, соединенных ветвями дерева.[41]
Дуалы не могут быть сформированы для каждого графа. Двойственность требует, чтобы каждый набор связей имел набор двойных разрезов в дуальном графе. Это условие выполняется тогда и только тогда, когда граф отображается на сфере без пересечения ветвей. Чтобы увидеть это, обратите внимание, что требуется набор связей, чтобы «связать» график на две части, а его двойное, набор разрезов, требуется для разрезания графа на две части. Граф конечной сети, которая не будет отображаться на сфере, потребует п-кратный тор. Связка, проходящая через отверстие в торе, не сможет разделить граф на две части. Следовательно, дуальный граф не будет разрезан на две части и не будет содержать требуемого множества разрезов. Следовательно, только плоские графы имеют двойники.[42]
Дуалы также не могут быть сформированы для сетей, содержащих взаимные индуктивности так как соответствующего емкостного элемента нет. Могут быть разработаны эквивалентные схемы, у которых есть двойники, но двойники не могут быть сформированы напрямую из взаимной индуктивности.[43]
Удаление узлов и сеток
Операции над набором сетевых уравнений имеют топологическое значение, которое может помочь визуализировать происходящее. Устранение напряжения узла из набора сетевых уравнений топологически соответствует исключению этого узла из графа. Для узла, подключенного к трем другим узлам, это соответствует хорошо известному Y-Δ преобразование. Преобразование может быть расширено до большего числа подключенных узлов и тогда известно как преобразование преобразование звездообразной сетки.[44]
Обратным к этому преобразованию является преобразование Δ-Y, которое аналитически соответствует устранению тока сетки и топологически соответствует устранению сетки. Однако устранение тока сетки, сетка которого имеет общие ветви с произвольным числом других сеток, в общем случае не приведет к реализуемому графу. Это связано с тем, что график преобразования общей звезды - это график, который не отображается на сферу (он содержит звездные многоугольники и, следовательно, несколько кроссоверов). Двойник такого графа не может существовать, но это граф, необходимый для представления исключения обобщенной сетки.[44]
Взаимная связь

В обычном графическом представлении схем нет средств явного представления взаимных индуктивных связей, таких как трансформатор, и такие компоненты могут привести к отключенный граф с более чем одной отдельной частью. Для удобства анализа граф с несколькими частями можно объединить в один граф, объединив по одному узлу в каждой части в один узел. Это не влияет на теоретическое поведение схемы, поэтому проведенный анализ остается в силе. Тем не менее, если бы схема была реализована таким образом, это имело бы практическое значение, поскольку это разрушило бы изоляцию между частями. Примером может служить трансформатор, заземленный как на первичной, так и на вторичной стороне. Трансформатор по-прежнему работает как трансформатор с тем же соотношением напряжений, но теперь его нельзя использовать как трансформатор. разделительный трансформатор.[45]
Более современные методы в теории графов могут иметь дело с активными компонентами, что также проблематично в традиционной теории. Эти новые методы также могут иметь дело с взаимными связями.[46]
Активные компоненты
Существует два основных подхода к работе с взаимными связями и активными компонентами. В первом из них Сэмюэл Джефферсон Мейсон в 1953 г. введен графики потока сигналов.[47] Графы потоков сигналов - это взвешенные ориентированные графы. Он использовал их для анализа схем, содержащих взаимные связи и активные сети. Вес направленного ребра на этих графиках представляет собой усиление, например, имеющееся у усилителя. В общем, графы потока сигналов, в отличие от описанных выше регулярных ориентированных графов, не соответствуют топологии физического расположения компонентов.[46]
Второй подход - расширить классический метод, включив в него взаимные связи и активные компоненты. Для этого было предложено несколько методов. В одном из них построены два графика: один представляет токи в цепи, а другой - напряжения. Пассивные компоненты будут иметь одинаковые ветви в обоих деревьях, а активные компоненты - нет. Метод основан на идентификации остовных деревьев, общих для обоих графов. Альтернативный метод расширения классического подхода, который требует только одного графа, был предложен Ченом в 1965 году.[примечание 5] Метод Чена основан на укоренившееся дерево.[46]
Гиперграфы
Другой способ расширения классической теории графов для активных компонентов - использование гиперграфы. Некоторые электронные компоненты не представлены в графическом виде. В транзистор имеет три точки подключения, но нормальная ветвь графа может подключаться только к двум узлам. Современное интегральные схемы иметь гораздо больше связей, чем это. Эту проблему можно решить, используя гиперграфы вместо обычных графов.[48]

В традиционном представлении компоненты представлены ребрами, каждое из которых соединяется с двумя узлами. В гиперграфе компоненты представлены гиперребра который может подключаться к произвольному количеству узлов. У гиперребер есть щупальца которые соединяют гиперребро с узлами. Графическое представление гиперребра может быть прямоугольником (по сравнению с ребром, которое является линией), а изображения его щупалец - линиями от прямоугольника до соединенных узлов. В направленном гиперграфе щупальца несут метки, которые определяются меткой гиперребра. Обычный ориентированный граф можно представить как гиперграф с гиперребрами, каждое из которых имеет два щупальца. Эти два щупальца помечены источник и цель и обычно обозначается стрелкой. В общем гиперграфе с большим количеством щупалец потребуется более сложная маркировка.[49]
Гиперграфы могут быть охарактеризованы их матрицами инцидентности. Регулярный граф, содержащий только двухконцевые компоненты, будет иметь ровно два ненулевых элемента в каждой строке. Любая матрица инцидентности с более чем двумя ненулевыми элементами в любой строке является представлением гиперграфа. Количество ненулевых записей в строке - это классифицировать соответствующей ветви, а наивысший ранг ветви - это ранг матрицы инцидентности.[50]
Неоднородные переменные
Классический сетевой анализ разрабатывает набор сетевых уравнений, сетевые переменные которых однородны либо по току (анализ петли), либо по напряжению (анализ узлов). Найденный таким образом набор сетевых переменных не обязательно является минимумом, необходимым для формирования набора независимых уравнений. Может быть разница между количеством переменных в циклическом анализе и в анализе узлов. В некоторых случаях минимально возможное количество может быть меньше любого из этих значений, если требование однородности ослаблено и допускается сочетание переменных тока и напряжения. Результат Киси и Катаджини в 1967 году[примечание 6] состоит в том, что абсолютное минимальное количество переменных, необходимых для описания поведения сети, задается максимальным расстоянием[примечание 7] между любыми двумя промежутками леса[примечание 8] сетевого графа.[46]
Сетевой синтез
Теорию графов можно применить к сетевой синтез. Классический сетевой синтез реализует требуемую сеть в одном из ряда канонические формы. Примеры канонических форм - это реализация импеданс ведущей точки канонической лестничной сетью Кауэра, или канонической формой Фостера, или реализацией Бруна иммитанс от его положительно-вещественные функции. С другой стороны, топологические методы не исходят из данной канонической формы. Скорее, форма является результатом математического представления. Некоторые канонические формы требуют для своей реализации взаимной индуктивности. Основная цель топологических методов синтеза сети состоит в том, чтобы устранить необходимость в этих взаимных индуктивностях. Одна теорема, которую следует вывести из топологии, заключается в том, что реализация полного сопротивления точки возбуждения без взаимных связей минимальна тогда и только тогда, когда нет контуров, полностью состоящих из индукторов или конденсаторов.[51]
Теория графов наиболее эффективна в синтезе сетей, когда элементы сети могут быть представлены действительными числами (одноэлементные сети, такие как резистивные сети) или двоичными состояниями (например, коммутационные сети).[46]
Бесконечные сети
Возможно, самой ранней изучаемой сетью с бесконечным графом была лестничная сеть, которая использовалась для представления линии передачи в окончательном виде разработан Оливер Хевисайд в 1881 году. Конечно, все ранние исследования бесконечных сетей ограничивались периодическими структурами, такими как лестницы или сетки с одними и теми же элементами, повторяющимися снова и снова. Инструменты для анализа бесконечных сетей с произвольной топологией стали доступны только в конце 20 века.[52]
Бесконечные сети представляют в основном только теоретический интерес и являются игрушкой математиков. Бесконечные сети, не ограниченные реальными ограничениями, могут обладать некоторыми очень нефизическими свойствами. Например, в некоторых случаях законы Кирхгофа могут не сработать, и можно определить бесконечные лестницы резисторов, которые имеют импеданс точки возбуждения, который зависит от оконечной нагрузки на бесконечности. Еще одно нефизическое свойство теоретических бесконечных сетей состоит в том, что они, как правило, рассеивают бесконечную мощность, если на них не накладываются ограничения в дополнение к обычным сетевым законам, таким как законы Ома и Кирхгофа. Однако есть несколько реальных приложений. Пример линии передачи - это одна из класса практических задач, которые можно моделировать бесконечно малыми элементами ( модель с распределенными элементами ). Другие примеры - запуск волн в сплошную среду, окаймляющее поле проблемы и измерение сопротивления между точками подложки или в скважину.[53]
Трансфинитные сети еще больше расширяют идею бесконечных сетей. К узлу на конце бесконечной сети может быть подключена еще одна ветвь, ведущая в другую сеть. Эта новая сеть может быть бесконечной. Таким образом, могут быть построены топологии, имеющие пары узлов без конечных дорожка между ними. Такие сети бесконечных сетей называются трансфинитными сетями.[54]
Примечания
- ^ Хомут-цепи. Терминология, созданная Артур Кэли. Хомуты - это параллельные ответвления, а цепи - это последовательные ответвления. (Мак-Магон, 1891, стр. 330) Отдельное ответвление можно рассматривать как ярмо или цепь.
- ^ Набор галстуков. Период, термин набор галстуков был придуман Эрнст Гийемен (Гийемен, стр. Xv). Гийемен говорит, что это имя было выбрано потому, что если бы ветви набора галстуков были уменьшены до нулевой длины, график стал бы «привязанным», как сетка с шнурком (Guillemin, p.17).
Гийемен был ведущей фигурой в разработке и обучении линейному сетевому анализу (Wildes and Lindgren, pp.154–159). - ^ Сетка. Сетка - это петля, не содержащая никаких других петель.
- ^ Лабиринт. Этот термин - еще одно изобретение Гийемена (Guillemin, p.xv). Назван так потому, что пробелы в графе, через которые проходят ссылки, имеют форму лабиринта-головоломки.
- ^ Чен, Вай-Кай., «Топологический анализ активных сетей», IEEE Transactions по теории цепей, vol.13, Iss.4, pp.438–439, December 1966.
- ^ Краткое изложение этой работы было впервые представлено на сайте;
- Киши, Женя; Кадзитани, Ёдзи, «О максимально различных деревьях», Пятая ежегодная конференция Аллертона по теории цепей и систем, pp.635–643, 1967.
- ^ Расстояние между деревьями определяется как количество ребер, которые находятся в одном дереве, но отсутствуют в другом. То есть это количество ребер, которое необходимо изменить, чтобы превратить одно дерево в другое (Киши и Каджитани, стр. 323).
- ^ Охватывающий лес. Лес деревьев, в котором каждый узел графа посещается одним из деревьев.
Смотрите также
Рекомендации
- ^ Тули, стр. 258–264.
- ^ Гийемен, стр. 5–6.
- ^ Мак-Магон (1891), стр. 331
- ^ Фараго, стр.18–21.
Редифон, стр.22 - ^ Редифон, стр.22
- ^ Фараго, стр.112–116.
Редифон, стр.45–48 - ^ Фараго, стр.117–118
- ^ Фараго, стр. 125–127.
- ^ Кэмпбелл, стр. 5–6, Кинд и Фессер, стр. 29–30
- ^ Кэмпбелл, стр.5–6, 20
- ^ Фараго, стр. 98–134.
- ^ Суреш, стр.483–484, 530–532
- ^ Кирхгоф, Г. (1847) "Über die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Ströme geführt wird" (О решении уравнений, к которым приводит исследование линейного распределения гальванических токов), Annalen der Physik und Chemie, 72 (12) : 497–508.
- ^ Джеймс Клерк Максвелл, Трактат об электричестве и магнетизме (Оксфорд, Англия: Clarendon Press, 1873), т. 1, часть II, «О линейных системах проводников в целом», С. 333–336.
- ^ Ватару Майеда и Сундарам Сешу (ноябрь 1957 г.) «Топологические формулы для сетевых функций», Бюллетень инженерной экспериментальной станции Университета Иллинойса, вып. 446, стр. 5.
- ^ Х. Пуанкаре (1900) "Второе дополнение к l'Analysis Situs", Труды Лондонского математического общества, 32 : 277–308. Доступно в Интернете по адресу: Mocavo.com
- ^ Освальд Веблен, Кембриджский коллоквиум, 1916 г., (Нью-Йорк: Американское математическое общество, 1918-1922), том 5, стр. 2: Analysis Situs, «Матрицы ориентации», стр. 25-27.
- ^ а б c Седербаум, стр.64
- ^ Фостер, с.309.
Фостер и Кэмпбелл, стр.232. - ^ Гийемен, стр.5
- ^ Гийемен, стр. 5–6.
Суреш, стр.485 - ^ Гийемен, стр.5
Минас, стр.213–214
Суреш, стр.485 - ^ Суреш, стр 485, 487–489
- ^ Фостер, стр.310
- ^ Гийемен, стр.6-7
Фостер, стр.310 - ^ Гийемен, стр. 7
Суреш, стр. 486 - ^ Гийемен, стр.8–9
- ^ Гийемен, стр.9–10
- ^ Гийемен, стр.10–17.
- ^ Гийемен, стр.23–27.
Суреш стр.514 - ^ Гийемен, стр.17–23
- ^ Гийемен, стр.43
Суреш, стр.518, стр.523–528 - ^ Фостер, стр. 310–311.
- ^ Фостер, стр. 312–313.
- ^ Гийемен, стр.64–81
- ^ Гийемен, стр.112–116
- ^ Гийемен, стр.116–120
- ^ Гийемен, стр.44
Суреш, стр. 516–517 - ^ Гийемен, стр.49–50
Суреш, стр.517 - ^ Гийемен, стр.43–44
Фостер, стр. 313 - ^ Гийемен, стр.51–53
- ^ Гийемен, стр.535
Суреш, стр.517 - ^ Гийемен, стр.536
- ^ а б Гийемен, стр. 127–132.
- ^ Гийемен, стр.6–7
- ^ а б c d е Седербаум, стр.65
- ^ Сэмюэл Дж. Мейсон (сентябрь 1953 г.) "Теория обратной связи - Некоторые свойства графов потока сигналов", Труды I.R.E., 41 (9) : 1144–1156.
- ^ Минас, стр.213
- ^ Минас, стр.213–214
- ^ Скиена, стр.382
- ^ Седербаум, стр.67
- ^ Бриттен, стр.39
Земанский, p.vii - ^ Zemanian, pp.vii-ix, 17–18, 24–26
- ^ Земанский, p.x
Библиография
- Бриттен, Джеймс Э., Введение в загрузочную катушку: Джордж А. Кэмпбелл и Майкл И. Пупин ", Технологии и культура, т. 11, нет. 1, стр. 36–57, издательство Университета Джона Хопкинса, январь 1970 г. Дои:10.2307/3102809.
- Кэмпбелл, Г. А., «Физическая теория электрического волнового фильтра», Технический журнал Bell System, Ноябрь 1922 г., т. 1, вып. 2. С. 1–32.
- Седербаум, И., «Некоторые приложения теории графов к сетевому анализу и синтезу», Транзакции IEEE в схемах и системах, том 31, Issue 1, pp. 64–68, январь 1984.
- Фараго, П. С., Введение в линейный сетевой анализ, The English Universities Press Ltd, 1961.
- Фостер, Рональд М., «Геометрические схемы электрических сетей», Труды Американского института инженеров-электриков, том 51, Issue 2, pp. 309–317, июнь 1932 г.
- Фостер, Рональд М .; Кэмпбелл, Джордж А., «Максимальные выходные сети для цепей телефонной подстанции и ретранслятора», Труды Американского института инженеров-электриков, том 39, Iss.1, pp. 230–290, январь 1920.
- Гийемен, Эрнст А., Теория вводных схем, Нью-Йорк: John Wiley & Sons, 1953 г. OCLC 535111
- Добрый, Дитер; Фесер, Курт, Методы высоковольтных испытаний, переводчик Ю. Нараяна Рао, Newnes, 2001 ISBN 0-7506-5183-0.
- Киши, Женя; Каджитани, Ёдзи, «Максимально удаленные деревья и главное разбиение линейного графа», IEEE Transactions по теории цепей, том 16, Iss.3, pp. 323–330, август 1969.
- Мак-Магон, Перси А., «Хомуты и составы из нескольких частей в связи с аналитическими формами, называемыми« Деревья »», Труды Лондонского математического общества, том 22 (1891), стр.330–346 Дои:10.1112 / плмс / с1-22.1.330.
- Мак-Магон, Перси А., «Комбинации сопротивлений», Электрик, том 28, pp. 601–602, 8 апреля 1892 г.
Перепечатано в Дискретная прикладная математика, том 54, вып. 2–3, с. 225–228, 17 октября 1994 г. Дои:10.1016 / 0166-218X (94) 90024-8. - Минас, М., "Создание семантических представлений диаграмм", Применение преобразований графов с промышленным значением: международный семинар, AGTIVE'99, Керкраде, Нидерланды, 1–3 сентября 1999 г .: материалы, стр. 209–224, Springer, 2000 г. ISBN 3-540-67658-9.
- Радио-дневник Redifon, 1970, William Collins Sons & Co, 1969.
- Скиена, Стивен С., Руководство по разработке алгоритмов, Springer, 2008 г., ISBN 1-84800-069-3.
- Суреш, Кумар К. С., «Введение в топологию сети», глава 11 в Электрические схемы и сети, Pearson Education India, 2010 г. ISBN 81-317-5511-8.
- Тули, Майк, BTEC First Engineering: обязательные и избранные дополнительные модули для BTEC First in Engineering, Рутледж, 2010 г. ISBN 1-85617-685-1.
- Wildes, Karl L .; Линдгрен, Нило А., "Сетевой анализ и синтез: Эрнст А. Гийемин", Век электротехники и информатики в Массачусетском технологическом институте, 1882–1982 гг., стр. 154–159, MIT Press, 1985 ISBN 0-262-23119-0.
- Земанян, Армен Х., Бесконечные электрические сети, Издательство Кембриджского университета, 1991 г. ISBN 0-521-40153-4.





