Геометрия такси - Taxicab geometry

А геометрия такси это форма геометрия в котором обычная функция расстояния или метрика из Евклидова геометрия заменяется новой метрикой, в которой расстояние между двумя точками - это сумма абсолютные различия от их Декартовы координаты. В метрика такси также известен как прямолинейное расстояние, L1 расстояние, L1 расстояние или норма (увидеть Lп Космос ), змея расстояние, расстояние до городского квартала, Манхэттенское расстояние или Манхэттенская длина, с соответствующими вариациями в названии геометрии.[1] Последние имена ссылаются на сетка большинства улиц на острове Манхэттен, который определяет кратчайший путь, по которому машина может пройти между двумя перекрестками в район иметь длину, равную расстоянию перекрестков в геометрии такси.
Геометрия использовалась в регрессивный анализ с 18 века, и сегодня его часто называют ЛАССО. Геометрическая интерпретация датируется неевклидова геометрия 19 века и связано с Герман Минковски.
Формальное определение
Расстояние такси, , между двумя векторами в п-размерный настоящий векторное пространство с фиксированной Декартова система координат, - сумма длин выступов отрезок между точками на оси координат. Более формально
где находятся векторов
Например, в самолет, расстояние такси между и является
Свойства
Расстояние такси зависит от вращение системы координат, но не зависит от ее отражение вокруг координатной оси или ее перевод. Геометрия такси удовлетворяет всем Аксиомы Гильберта (формализация Евклидова геометрия ) за исключением аксиома стороны-угла-стороны, поскольку два треугольника с одинаковыми «длинными» сторонами и одинаковым углом между ними обычно не конгруэнтный если только указанные стороны не параллельны.
Круги
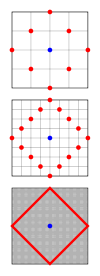
А круг представляет собой набор точек с фиксированным расстоянием, называемый радиус, из точки, называемой центр. В геометрии такси расстояние определяется другой метрикой, чем в евклидовой геометрии, и форма кругов также изменяется. Круги такси квадраты со сторонами, ориентированными под углом 45 ° к осям координат. На изображении справа показано, почему это так, красным цветом показаны все точки с фиксированным расстоянием от центра, показанные синим цветом. По мере уменьшения размеров городских кварталов количество точек становится больше, и они превращаются в повернутый квадрат в непрерывной геометрии такси. Хотя каждая сторона будет иметь длину с помощью Евклидова метрика, где р - радиус круга, его длина в геометрии такси равна 2р. Таким образом, длина окружности равна 8р. Таким образом, значение геометрического аналога равно 4 в этой геометрии. Формула для единичного круга в геометрии такси: в Декартовы координаты и
Окружность радиуса 1 (на этом расстоянии) - это район фон Неймана своего центра.
Круг радиуса р для Чебышевская дистанция (L∞ метрика ) на плоскости также есть квадрат со стороной 2р параллельно осям координат, поэтому планарное расстояние Чебышева можно рассматривать как эквивалентное путем вращения и масштабирования до планарного расстояния такси. Однако эта эквивалентность L1 и я∞ показатели не распространяются на более высокие измерения.
Всякий раз, когда каждая пара в наборе этих кругов имеет непустое пересечение, существует точка пересечения для всего набора; следовательно, расстояние Манхэттена образует инъективное метрическое пространство.
Приложения
Меры дистанций в шахматах
В шахматы, расстояние между квадратами на шахматная доска для грачи измеряется расстоянием такси; короли и королевы использовать Чебышевская дистанция, и епископы используйте расстояние такси (между квадратами одного цвета) на шахматной доске, повернутой на 45 градусов, то есть с ее диагоналями в качестве осей координат. Чтобы добраться от одной клетки до другой, только короли требуют, чтобы количество ходов было равно их соответствующему расстоянию; для ладей, ферзей и слонов требуется один-два хода (на пустой доске и при условии, что этот ход вообще возможен в случае слона).
Сжатое зондирование
При решении недоопределенная система линейных уравнений регуляризация член для вектора параметров выражается через -норма (геометрия такси) вектора.[2] Этот подход появляется в структуре восстановления сигнала, называемой сжатое зондирование.
Отличия частотных распределений
Геометрию такси можно использовать для оценки различий в дискретных частотных распределениях. Например, в Сплайсинг РНК позиционное распределение гексамеры, которые показывают вероятность появления каждого гексамера в каждом заданном нуклеотид рядом с местом стыка, можно сравнить с расстоянием L1. Каждое распределение положений может быть представлено в виде вектора, где каждая запись представляет вероятность того, что гексамер начинается с определенного нуклеотида. Большое расстояние L1 между двумя векторами указывает на значительную разницу в характере распределений, в то время как небольшое расстояние указывает на распределения схожей формы. Это эквивалентно измерению площади между двумя кривыми распределения, поскольку площадь каждого сегмента представляет собой абсолютную разницу между вероятностями двух кривых в этой точке. При суммировании для всех сегментов он дает ту же меру, что и расстояние L1.[3]
История
В L1 метрика использовалась в регрессивный анализ в 1757 г. Роджер Джозеф Боскович.[4] Геометрическая интерпретация датируется концом 19 века и развитием неевклидовы геометрии, в частности Герман Минковски и его Неравенство Минковского, из которых эта геометрия является частным случаем, особенно используемым в геометрия чисел, (Минковский 1910 ). Формализация Lп пробелы зачисляется на (Рис 1910 ).
Смотрите также
- Нормированное векторное пространство
- Метрическая
- Ортогональная выпуклая оболочка
- Расстояние Хэмминга
- Пятнадцать пазлов
- Случайная прогулка
- Электропроводка на Манхэттене
Заметки
- ^ Блэк, Пол Э. "Манхэттенское расстояние". Словарь алгоритмов и структур данных. Получено 6 октября, 2019.
- ^ Донохо, Дэвид Л. (23 марта 2006 г.). "Для большинства больших недоопределенных систем линейных уравнений минимальный -нормальное решение также является самым редким решением ". Сообщения по чистой и прикладной математике. 59 (6): 797–829. Дои:10.1002 / cpa.20132.
- ^ Лим, Киан Хуат; Феррарис, Лучиана; Filloux, Madeleine E .; Рафаэль, Бенджамин Дж .; Fairbrother, Уильям Г. (5 июля 2011 г.). «Использование позиционного распределения для идентификации элементов сплайсинга и прогнозирования дефектов процессинга пре-мРНК в генах человека». Труды Национальной академии наук Соединенных Штатов Америки. 108 (27): 11093–11098. Bibcode:2011PNAS..10811093H. Дои:10.1073 / pnas.1101135108. ЧВК 3131313. PMID 21685335.
- ^ Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 г.. Издательство Гарвардского университета. ISBN 9780674403406. Получено 6 октября, 2019.
использованная литература
- Краузе, Юджин Ф. (1987). Геометрия такси. Дувр. ISBN 978-0-486-25202-5.
- Минковский, Германн (1910). Geometrie der Zahlen (на немецком). Лейпциг и Берлин: Р. Г. Тойбнер. JFM 41.0239.03. Г-Н 0249269. Получено 6 октября, 2019.
- Рис, Фриджес (1910). "Untersuchungen über Systeme integrierbarer Funktionen". Mathematische Annalen (на немецком). 69 (4): 449–497. Дои:10.1007 / BF01457637. HDL:10338.dmlcz / 128558.
внешние ссылки
- Вайсштейн, Эрик В. «Метрика такси». MathWorld.
- Малькевич, Джо (1 октября 2007 г.). "Такси!". Американское математическое общество. Получено 6 октября, 2019.














