Рациональная тригонометрия - Rational trigonometry
Эта статья может содержать чрезмерное количество сложных деталей, которые могут заинтересовать только определенную аудиторию. (Февраль 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Рациональная тригонометрия предлагаемая переформулировка метрический планарный и твердые геометрии (который включает тригонометрия ) канадским математиком Норманом Дж. Вильдбергером, в настоящее время профессором математики в Университет Нового Южного Уэльса. Его идеи изложены в его книге 2005 года. Божественные пропорции: от рациональной тригонометрии к универсальной геометрии.[1] В соответствии с Новый ученый, отчасти его мотивация к альтернативе традиционной тригонометрии заключалась в том, чтобы избежать некоторых проблем, которые, как он утверждает, возникают при использовании бесконечных рядов в математике. Рациональная тригонометрия избегает прямого использования трансцендентные функции подобно синус и косинус подставив их эквиваленты в квадрате.[2] Вильдбергер черпает вдохновение у математиков, предшествовавших Георг Кантор с бесконечная теория множеств, подобно Гаусс и Евклид, которые, как он утверждает, были гораздо более осторожны в использовании бесконечных множеств, чем современные математики.[2][nb 1] На сегодняшний день рациональная тригонометрия в значительной степени не упоминается в основной математической литературе.
Подход
Рациональная тригонометрия следует подходу, основанному на методах линейная алгебра к темам начальной (старшей школы) геометрии. Расстояние заменяется его значением в квадрате (квадранс) и 'угол 'заменяется квадратом обычного синус соотношение (распространять), связанный с любым углом между двумя линиями. (The дополнять распространения, известного как Пересекать, также соответствует масштабированной форме внутренний продукт между отрезками, взятыми как векторов ). Три основных закона в тригонометрии - Теорема Пифагора, то синус закон и закон косинуса - даны в рациональной (эквивалентной квадрату) форме и дополнены двумя дополнительными законами - формула тройной четверки (связывающие квадранты трех коллинеарных точек) и формула тройного спреда (связывая спреды трех параллельных линий) -, что дает пять основных законов предмета.[нужна цитата ]
В остальном рациональная тригонометрия в целом основана на декартовой аналитической геометрии с точка определяется как упорядоченная пара рациональное число
и линия
как генерал линейное уравнение с рациональными коэффициентами а, б и c.
Избегая вычислений, основанных на квадратный корень операции, дающие только приблизительный расстояния между точками или стандартные тригонометрические функции (и их обратные), дающие только усеченные многочлен приближения геометрия углов (или их проекций) становится полностью алгебраической. Другими словами, нет никаких предположений о существовании настоящий номер решения проблем, с результатами вместо этого даны по полю рациональных чисел, их расширения алгебраических полей, или же конечные поля. Утверждается, что после этого многие классические результаты из Евклидова геометрия применимо в рациональный формы (как квадратичные аналоги) над любым полем не характеристика два.[нужна цитата ]
Книга Божественные пропорции показывает применение исчисления с использованием рациональных тригонометрических функций, включая вычисления трехмерных объемов. Он также имеет дело с применением рациональной тригонометрии к ситуациям, связанным с иррациональными явлениями, например, с доказательством того, что все Платоновы тела имеют рациональные «разносы» между гранями.[nb 2]
Известность и критика
Рациональная тригонометрия (RT) упоминается лишь в небольшом количестве математических публикаций, помимо собственных статей и книги Вильдбергера. Божественные пропорции был уволен рецензентом Полом Дж. Кэмпбеллом в Математический журнал из Математическая ассоциация Америки (MAA): «автор утверждает, что эта новая теория займет« менее половины обычного времени, чтобы изучить »; но я сомневаюсь в этом. И ее все равно придется согласовывать с традиционными концепциями и обозначениями». Рецензент Уильям Баркер, профессор математики Крыла Исаака Генри в Bowdoin College, также писавший для MAA, был более одобряющим: "Божественные пропорции несомненно, ценное дополнение к математической литературе. В нем тщательно разрабатывается наводящий на размышления, умный и полезный альтернативный подход к тригонометрии и евклидовой геометрии. Было бы неудивительно, если бы некоторые из его методов в конечном итоге просочились в стандартную разработку этих предметов. Однако, если не произойдет неожиданного сдвига в общепринятых взглядах на основы математики, нет веских оснований для рациональной тригонометрии заменить классическую теорию ». [3] Новый ученый 's Аманда Гефтер описала подход Вильдбергера как пример финитизм.[2] Джеймс Франклин в Математический интеллигент утверждал, что книга заслуживает внимательного рассмотрения.[4]
Анализ Майклом Гилсдорфом примеров проблем, приведенный Вильдбергером в ранней статье, оспаривает утверждение, что RT требуется меньше шагов для решения наиболее проблемы, если свободный выбор классических методов (например,формула шнурка 'для площади треугольника по координатам его вершин или применяя частный случай теоремы Стюарта непосредственно к треугольнику с медианой) позволяет оптимизировать решение задач. Относительно педагогики и использования квадратичных величин, введенных RT предлагает реальные преимущества по сравнению с традиционным обучением, автор заметил, что классическая тригонометрия изначально не была основана на использовании Серия Тейлор для аппроксимации углов вообще, а скорее на измерениях аккорд (в два раза больше синуса угла), и, таким образом, при правильном понимании студенты могли бы получить постоянные преимущества от использования линейных измерений без заявленных логичный несоответствия при последующем введении круговой параметризации по углу.[5]
Квадранс
Евклидово расстояние и квадрат евклидова расстояния (называемые «квадранс» в рациональной тригонометрии) оба измеряют разделение точек в евклидовом пространстве.[6] Следуя теореме Пифагора, квадранс двух точек А1 = (Икс1, у1) и А2 = (Икс2, у2) в плоскости определяется как сумма квадратов разностей и координаты:
В неравенство треугольника выражается в рациональной тригонометрии как .
Распространять

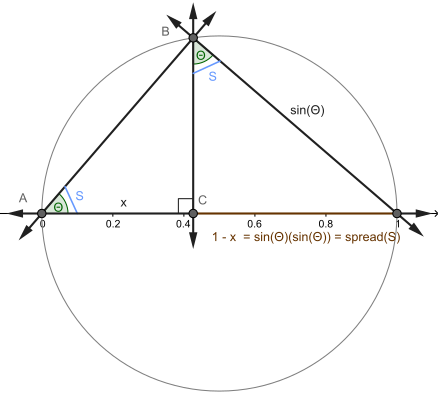
Спред дает одну меру разделения двух строк как единой безразмерное число В диапазоне [0,1] (из параллельно к перпендикуляр) для евклидовой геометрии. Он заменяет концепцию угла (и имеет несколько отличий от него), обсуждаемую в следующем разделе. Описание распространения может включать:
- Тригонометрический (самый элементарный): коэффициент синуса квадрантов в прямоугольном треугольнике, что эквивалентно квадрату синуса угла (оставили).[6] Расширяя прилегающую сторону AC стать частью единица измерения диаметр в окружности и учитывая подобные треугольники (верно), спред можно измерить как длина (или же соотношение к диаметру) внешнего сегмента - более традиционно равный половине раза (1 минус косинус из вдвое больший угол А ) или же гаверсин.
- Вектор: как рациональная функция склоны (и относительный направление) пары линий, где они встречаются.
- Декартово: как рациональная функция три координаты, используемые для приписывания два векторов.
- Линейная алгебра (от скалярное произведение): нормализованная рациональная функция: площадь то детерминант двух векторов (или пары пересекающихся прямых), образующих матрица разделены на продукт их квадранты.
Расчет спреда
Тригонометрический
Предположим две строки, л1 и л2, пересекаются в точке А как показано справа. Выберите точку B ≠ А на л1 и разреши C быть основанием перпендикуляра от B к л2. Тогда распространение s является[6]
Вектор / наклон (с двумя переменными)
Как и угол, разброс зависит только от относительного наклона двух линий (постоянные члены исключаются) и инвариантен при переносе (то есть сохраняется, когда линии перемещаются параллельно самим себе). Итак, учитывая две строки, уравнения которых
мы можем переписать их как две линии, которые встречаются в начале координат (0, 0) с уравнениями
В этом положении точка (−б1, а1) удовлетворяет первому уравнению и (−б2, а2) удовлетворяет второму и трем пунктам (0, 0), (−б1, а1) и (−б2, а2) формирование разворота даст три квадранта:
В перекрестный закон - см. Ниже - по спреду
который становится:
В числителе это упрощает: (2а1а2 + 2б1б2)2, давая:
(Примечание: 1 − s это выражение для Пересекать, квадрат косинуса любого угла между парой линий или векторов, который дает название перекрестный закон.)
Затем, используя Тождество Брахмагупты – Фибоначчи
стандартное выражение для разброса по наклонам (или направлениям) двух линий становится
В этой форме (и в его декартовом эквиваленте, который следует далее) разброс - это отношение квадрата определителя двух векторов (числитель) к произведению их квадрантов (знаменатель).
Декартово (с тремя переменными)
Для треугольника, в отличие от пары линий или векторов, мы можем заменить точки (−б1, а1) , (−б2, а2) и '(0, 0)' в предыдущем результате с (Икс1,у1) , (Икс2, у2) и (Икс3, у3) чтобы получить спред в соответствующей вершине:
который в форме симметричного числителя принимает следующий вид:
и, следовательно, для других связанных спредов s1 и s2:
Разброс по сравнению с углом

В отличие от угла, который может определять отношение между лучи исходящий из точки, измерение дуги параметризации, и там, где пара линий может рассматриваться как четыре пары лучей, образующих четыре угла, `` распространение '' является более фундаментальным в рациональной тригонометрии, описывая две строки одной мерой рациональной функции (см. выше).[6] Являясь эквивалентом квадрат из синус соответствующего угла θ (и к гаверсин из аккорд -основная двухугольная Δ = 2θ), разброс как угла, так и его дополнительный угол равны.
| Распространять | Угол (θ) | Количество | ||||
|---|---|---|---|---|---|---|
| грех2(θ) | Квадранты | Повороты | Радианы | Градусы | Gons | Единица измерения |
| 0 | 0 | 0 | 0 | 0° | 0грамм | |
| 1/4 | 1/3 | 1/12 | π/6 | 30° | 33+1/3грамм | |
| 1/2 | 1/2 | 1/8 | π/4 | 45° | 50грамм | |
| 3/4 | 2/3 | 1/6 | π/3 | 60° | 66+2/3грамм | |
| 1 | 1 | 1/4 | π/2 | 90° | 100грамм | ортогональные линии |
| 3/4 | 1+1/3 | 1/3 | 2π/3 | 120° | 133+1/3грамм | |
| 1/2 | 1+1/2 | 3/8 | 3π/4 | 135° | 150грамм | |
| 1/4 | 1+2/3 | 5/12 | 5π/6 | 150° | 166+2/3грамм | |
| 0 | 2 | 1/2 | π | 180° | 200грамм | |
Однако разброс не пропорционален расстоянию между линиями, как угол; со спредом 0, 1/4, 1/2, 3/4, а 1 соответствует неравномерно разнесенным углам 0 °, 30 °, 45 °, 60 ° и 90 °.
Вместо этого (вспоминая дополнительное свойство) два равных ко-терминальных спреда определяют третий спред, значение которого будет решением формулы тройного спреда для треугольника (или трех параллельных линий), имеющего спреды s, s и р:
дающий квадратичный многочлен (в s):
и решения
Это эквивалентно тригонометрическому тождеству:
углов θ, θ и 180° − 2θ треугольника, используя
для обозначения второй полином распространения в s.
При нахождении тройного спреда также используется формула тройного спреда как квадратное уравнение для неизвестного третьего спреда. т обработка известных спредов s и р (предыдущее решение) как константы. Оказывается (после исключения `` меньшего '' решения s) быть:
Дальнейшие кратные любому базовому разбросу строк могут быть сгенерированы либо путем продолжения использования формулы тройного распространения таким образом, либо путем использования формулы рекурсии (см. Ниже), которая применяет ее косвенно. В то время как любое рациональное кратное спреда будет полиномиальным в этом спреде (и, следовательно, рациональным), обратное не применяется. Например, по формула полуугла, две линии, встречающиеся под углом 15 ° (или 165 °), имеют разброс:
и, таким образом, существует посредством алгебраического расширения рациональных чисел.
Повернуть и повернуть
Этот раздел пуст. Вы можете помочь добавляя к этому. (Декабрь 2015 г.) |
Крутить
Этот раздел пуст. Вы можете помочь добавляя к этому. (Декабрь 2015 г.) |
Полиномы распространения
Как видно для двойных и тройных спредов, пth кратное любому спреду, s дает многочлен от этого разброса, обозначаемый Sп(s), как одно из решений формулы тройного спреда.
На общепринятом языке круговые функции, эти пя степень полиномы распространения, за п = 0, 1, 2, ..., можно охарактеризовать тождеством:[нужна цитата ]
Идентичности
Явные формулы
- (Майкл Хиршхорн, Шусян Го)[1]
- (М. Овдан)
- (М. Овдан)
Из определения сразу следует, что
- [нужна цитата ]
Формула рекурсии
Формула тройного спреда
- это тождество, элементы которого сами могут быть распределены полиномами вида:, и ,
Итак, взяв разницу (и переставив) выражения
- и
дает рекурсивный связь:
Связь с полиномами Чебышева
Полиномы разброса связаны с Полиномы Чебышева первого рода, Тп, тождеством
Из этого следует[1]
Второе равенство выше следует из тождества
о полиномах Чебышева.[нужна цитата ]
Сочинение
Полиномы распространения удовлетворяют композиционному тождеству[1]
Коэффициенты в конечных полях
Когда коэффициенты считаются членами конечное поле Fп, то последовательность {Sп}п = 0, 1, 2,... полиномов распространения периодичен с периодом п2 − 1/2. Другими словами, если k = п2 − 1/2, тогда Sп + k = Sп, для всехп.[нужна цитата ]
Ортогональность
Когда коэффициенты принимаются равными настоящий, то для п ≠ м, у нас есть[1]
За п = м, интеграл равен π/8 пока не п = м = 0, в этом случае этоπ/4.[нужна цитата ]
Производящие функции
Обычный производящая функция является
- (Майкл Хиршхорн)[1]
Экспоненциальная производящая функция:
- [нужна цитата ]
Дифференциальное уравнение
Sп(s) удовлетворяет линейному неоднородному дифференциальному уравнению второго порядка[нужна цитата ]
Теорема периодичности распространения
Для каждого целое число п и каждый основной п, Существует натуральное число м такой, что Sп(s) делится на п именно когда м разделяет п. этот номер м является делителем либо п − 1 или же п + 1. Доказательство этого теоретико-числового свойства было впервые дано в статье Шусян Го и Н. Дж. Вильдбергера.[7] Это предполагает рассмотрение проективного аналога квадранс в конечная проективная линия п1(Fп).
Таблица полиномов разброса с факторизацией
Первые несколько полиномов разброса следующие:
Законы рациональной тригонометрии
Вильдбергер утверждает, что в рациональной тригонометрии есть пять основных законов. Он также заявляет, что эти законы могут быть проверены с помощью математики средней школы. Некоторые из них эквивалентны стандартным тригонометрическим формулам с переменными, выраженными в квадранте и размахе.[6]
В следующих пяти формулах у нас есть треугольник, состоящий из трех точек. А1, А2, А3. Разброс углов в этих точках равен s1, s2, s3, и Q1, Q2, Q3, - квадранты сторон треугольника, противоположные А1, А2, А3, соответственно. Как и в классической тригонометрии, если мы знаем три из шести элементов s1, s2, s3, Q1, Q2, Q3, и эти трое не трое s, то мы можем вычислить остальные три.
Формула тройной четверки
Три точки А1, А2, А3 находятся коллинеарен если и только если:
куда Q1, Q2, Q3 представляют квадранты между А1, А2, А3 соответственно. Это может быть доказано либо аналитическая геометрия (предпочтительные средства в рамках рациональной тригонометрии) или производные от Формула Герона, используя условие коллинеарности, что треугольник, образованный тремя точками, имеет нулевую площадь.

Линия AB имеет общий вид:
где (неуникальные) параметры а, б, c можно выразить через координаты точек А и B в качестве:
так что везде на линии:
Но линия также может быть задана двумя одновременными уравнениями в параметре т, куда т = 0 в точке А и т = 1 в точке B:
или, исходя из исходных параметров:
Если точка C коллинеарен с точками А и B, существует некоторое значение т (для различных точек, не равных 0 или 1), назовите это λ, для которой эти два уравнения одновременно выполняются в координатах точки C, такое, что:
Теперь квадранты трех отрезков линии задаются квадратами разностей их координат, которые могут быть выражены через λ:
где использовался тот факт, что (−λ + 1)2 = (λ − 1)2.
Подставляя эти квадранты в доказываемое уравнение:
Сейчас если А и B представляют различные точки, такие что а2 + б2 ≠ 0, мы можем разделить обе стороны на Q(AB)2 = (а2 + б2)2:
Теорема Пифагора
Линии А1А3 (квадранс Q1) и А2А3 (квадранс Q2) перпендикулярны (их разброс равен 1) тогда и только тогда, когда:
куда Q3 это квадранс между А1 и А2.
Это эквивалентно теорема Пифагора (и его обратное).
Есть много классических доказательств Теорема Пифагора; этот оформлен в терминах рациональной тригонометрии.
В распространять угла - это квадрат его синус. Учитывая треугольник △ABC с разбросом 1 между сторонами AB и AC,
куда Q "квадранс", то есть квадрат расстояния.

Построить линию ОБЪЯВЛЕНИЕ разделив спред на 1, с точкой D онлайн до н.э, и сделав спред 1 с БД и ОКРУГ КОЛУМБИЯ. Треугольники △ABC, △DBA и △ЦАП похожи (имеют одинаковые спреды, но не одинаковые квадранты).
Это приводит к двум уравнениям для соотношений, основанных на размахе сторон треугольника:
Итак, в общем, два разворота, полученные в результате разделения спреда на две части, как линия ОБЪЯВЛЕНИЕ делает для распространения ТАКСИ, не суммируйте исходный спред, поскольку спред является нелинейной функцией. Итак, сначала мы доказываем, что деление спреда на 1 приводит к двум спредам, которые в сумме составляют исходный спред 1.
Для удобства, но без ограничения общности, ориентируем линии, пересекающиеся с разбросом 1, по осям координат, а разделяющую линию помечаем координатами (Икс1, у1) и (Икс2, у2). Тогда два спреда равны:
Следовательно
так что
Используя первые два соотношения из первой системы уравнений, это можно переписать:
Умножая обе стороны на Q(до н.э):
Закон распространения
Для любого треугольника △А1А2А3 с ненулевыми квадрантами:[1]
Это закон синуса, просто в квадрате.
Кросс закон
Для любого треугольника △А1А2А3,[1]
Это аналогично закон косинусов. Это называется «перекрестным законом», потому что (1 − s3), квадрат косинуса угла, называется крестом.
Формула тройного спреда
Для любого треугольника △А1А2А3,[1]
Это соотношение может быть получено из формулы для синус составного угла: в треугольнике (сумма трех углов которого равна 180 °) мы имеем,
- .
Эквивалентно, он описывает взаимосвязь между размахами трех параллельных линий, поскольку размах (например, угол) не изменяется, когда стороны треугольника перемещаются параллельно самим себе, чтобы встретиться в общей точке.
Знание двух спредов позволяет рассчитать третий путем решения соответствующей квадратной формулы. Поскольку производятся два решения, далее правила треугольного спреда необходимо использовать для выбора подходящего. Хотя это кажется более сложным, чем получение дополнительного угла непосредственно путем вычитания, иррациональное значение 'π'(неявно присутствующий в сумме углов треугольника) избегается.
Тригонометрия над произвольными полями
Поскольку законы рациональной тригонометрии задают алгебраические (а не трансцендентные) отношения, они в общем случае применяются к полям алгебраических чисел за пределами рациональных чисел. В частности, любое конечное поле, не имеющее характеристика 2 воспроизводит форму этих законов, и, следовательно, конечная геометрия поля.[8] "Плоскость", образованная конечным полем Fп это декартово произведение Fп × Fп всех упорядоченных пар элементов поля с противоположными отождествленными ребрами, образующими поверхность, топологически эквивалентную дискретизированной тор. Отдельные элементы соответствуют стандартным «точкам», а «линии» - наборам не более точки, связанные углом падения (начальная точка) плюс направление или наклон, заданные в наименьших терминах (скажем, все точки «2 сверху и 1 вверх»), которые «охватывают» плоскость перед повторением.
Пример: (проверьте закон распространения в F13)
На рисунке (справа) показан треугольник трех таких линий в условиях конечного поля F13 × F13:
Каждая линия имеет свой символ и точки пересечения линий (вершины) отмечен два символы присутствуют в точках:

- (2, 8), (9, 9) и (10, 0).
С помощью Теорема Пифагора с арифметикой по модулю 13, мы находим, что эти стороны имеют квадранты:
- (9 − 2)2 + (9 − 8)2 = 50 ≡ 11 мод 13
- (9 − 10)2 + (9 − 0)2 = 82 ≡ 4 мод 13
- (10 − 2)2 + (0 − 8)2 = 128 ≡ 11 мод 13
Преобразуя перекрестный закон как
дает отдельные выражения для каждого спреда в трех квадрантах:
- 1 − (4 + 11 − 11)2/4 × 4 × 11 = 1 − 3/7 ≡ 8 мод 13
- 1 − (11 + 11 − 4)2/4 × 11 × 11 = 1 − 12/3 ≡ 10 мод 13
- 1 − (4 + 11 − 11)2/4 × 4 × 11 = 1 − 3/7 ≡ 8 мод 13
В свою очередь, мы отмечаем, что все эти отношения равны - согласно закону распространения (по крайней мере, в модуле 13):
- 8/11 : 10/4 : 8/11
Поскольку первое и последнее соотношения совпадают (треугольник равнобедренный) мы просто перекрестно умножаем и берем разности, чтобы также показать равенство со средним соотношением:
- 11 × 10 - 8 × 4 = 78 ≡ 0 мод 13
В противном случае предполагается, что стандартная евклидова плоскость состоит только из рациональных точек, ℚ × ℚ, опуская любые неалгебраические числа в качестве решений. Такие свойства, как расположение объектов, представляющих решения или «содержание» геометрических теорем, поэтому следуют теоретико-числовому подходу, который отличается и является более ограничительным, чем подход, допускающий действительные числа. Например, не все Считается, что линии, проходящие через центр круга, пересекаются с окружностью на его окружности. Чтобы быть инцидентными, такие линии должны иметь форму
и обязательно встретить круг в рациональный точка.
Вычисления - сложность и эффективность
Рациональная тригонометрия позволяет решить почти все проблемы с помощью только сложения, вычитания, умножения или деления, поскольку тригонометрические функции (угла) целенаправленно избегаются в пользу тригонометрических соотношений в квадратичной форме.[6] Поэтому в лучшем случае результаты, требуемые как расстояние (или угол), могут быть аппроксимированы из точного рационального эквивалента квадранса (или разброса) после выполнения этих более простых операций. Однако, чтобы использовать это преимущество, каждая проблема должна быть задана или решена в терминах предшествующих квадрантов и спредов, что влечет за собой дополнительную работу.[9]
Законы рациональной тригонометрии, будучи алгебраическими, вносят тонкости в решения проблем, такие как неаддитивность квадрантов коллинеарных точек (через формулу тройного квадрата) или разброса совпадающих линий (через формулу тройного распространения), чтобы дать рациональное - ценные результаты. Напротив, в классическом предмете линейность включается в измерения расстояния и углов для упрощения этих операций, хотя и с помощью «трансцендентных» методов, использующих действительные числа что влечет за собой ориентировочную стоимость выпуска.
Смотрите также
Примечания
- ^ Взгляды Вильдбергера на историю бесконечности см. В статье Gefter New Scientist, а также в лекциях по истории математики и основам математики Вильдбергера, Университет Нового Южного Уэльса, около 2009–2014 гг., В более чем 120 видео и лекциях, доступных на сайте @youtube
- ^ Видеть Божественные пропорции для многочисленных примеров исчисления, выполненного с рациональными тригонометрическими функциями, а также проблем, связанных с применением рациональной тригонометрии к ситуациям, содержащим иррациональные числа.
Рекомендации
- ^ а б c d е ж грамм час я j Вильдбергер, Норман Джон (2005). Божественные пропорции: от рациональной тригонометрии к универсальной геометрии (1-е изд.). Австралия: Wild Egg Pty Ltd. ISBN 0-9757492-0-X. Получено 2015-12-01.
- ^ а б c "Конец бесконечности: пора отказаться от бесконечной истории? "Аманда Гефтер, New Scientist, 15 августа 2013 г.
- ^ http://www.maa.org/publications/maa-reviews/divine-proportions-rational-trigonometry-to-universal-geometry
- ^ Дж. Франклин, Обзор Божественные пропорции, Математический интеллигент 28 (3) (2006), 73-4.
- ^ http://web.maths.unsw.edu.au/~norman/papers/TrigComparison.pdf
- ^ а б c d е ж Вильдбергер, Норман Дж. (2007). «Рациональный подход к тригонометрии». Математические горизонты. Вашингтон, округ Колумбия: Математическая ассоциация Америки. Ноябрь 2007: 16–20. ISSN 1072-4117.
- ^ Шусян Го, Н. Дж. Вильдбергер (5 ноября 2009 г.). «Полиномы распространения, вращения и эффект бабочки». arXiv:0911.1025. Bibcode:2009arXiv0911.1025G. Цитировать журнал требует
| журнал =(помощь) - ^ Ле Ань Винь, Данг Фыонг Зунг (17 июля 2008 г.). «Явные жесткие графы Рамсея». arXiv:0807.2692. Bibcode:2008arXiv0807.2692V. Цитировать журнал требует
| журнал =(помощь), стр. 1. Другая версия этой статьи находится в Le Anh Vinh, Dang Phuong Dung (2008), "Явные жесткие графики Рамси В архиве 2012-10-11 в Wayback Machine ", Труды Международной конференции по отношениям, порядкам и графам: взаимодействие с компьютерными науками, 2008 г., Nouha Editions, 139–146. - ^ Ольга Кошелева (2008 г.) "Рациональная тригонометрия: вычислительная точка зрения "Геомбинаторика, Т. 1, № 1. С. 18–25.
Общие ссылки
- Сравнение классической и рациональной тригонометрии
- Рациональная тригонометрия в робототехнике, Жоао Пекито Алмейда
- Невозможность пересечения и угла с помощью линейки и циркуля: подход, использующий рациональную тригонометрию, Дэвид Дж. Пул
- Как умножать и делить треугольники, Морис Крейг
внешняя ссылка
- Сайт рациональной тригонометрии Вильдбергера, включая загружаемые статьи и разделы его книги
- Полиномы распространения, вращения и эффект бабочки
- Реализация рациональной тригонометрии в Euler Math Toolbox
















































![{ displaystyle { begin {align} S_ {0} (s) = {} & 0 [10pt] S_ {1} (s) = {} & s [10pt] S_ {2} (s) = { } & 4s-4s ^ {2} = {} & 4s (1-s) [10pt] S_ {3} (s) = {} & 9s-24s ^ {2} + 16s ^ {3} = {} & s (3-4 с) ^ {2} [10pt] S_ {4} (s) = {} & 16s-80s ^ {2} + 128s ^ {3} -64s ^ {4} = { } & 16 сек (1 сек) (1-2 сек) ^ {2} [10pt] S_ {5} (s) = {} & 25 сек-200 сек ^ {2} + 560 сек ^ {3} -640 сек ^ {4} + 256s ^ {5} = {} & s left (5-20s + 16s ^ {2} right) ^ {2} [10pt] S_ {6} (s) = {} & 36s-420s ^ {2} + 1792s ^ {3} -3456s ^ {4} + 3072s ^ {5} -1024s ^ {6} = {} & 4s (1s) (1-4s) ^ {2} (3- 4s) ^ {2} [10pt] S_ {7} (s) = {} & 49s-784s ^ {2} + 4704s ^ {3} -13440s ^ {4} + 19712s ^ {5} -14336s ^ { 6} + 4096 сек ^ {7} = {} & s left (7-56 сек + 112 сек ^ {2} -64 сек ^ {3} right) ^ {2} [10pt] S_ {8} (s ) = {} & 64s-1344s ^ {2} + 10752s ^ {3} -42240s ^ {4} + 90112s ^ {5} -106496s ^ {6} & {} + 65536s ^ {7} -16384s ^ { 8} = {} & 64s (s-1) (1-2s) ^ {2} left (1-8s + 8s ^ {2} right) ^ {2} [10pt] S_ {9} (s) = {} & 81s-2160s ^ {2} + 22176s ^ {3} -114048s ^ {4} + 329472s ^ {5} -559104s ^ {6} & {} + 552960s ^ {7} -294912s ^ {8} + 65536s ^ {9} = {} & s (-3 + 4s) ^ {2} left (-3 + 36s-96s ^ {2} + 64s ^ {3} right) ^ { 2} [10pt] S_ {10} (s) = {} & 100s-3300s ^ {2} + 42240s ^ {3} -274560s ^ {4} + 1025024s ^ {5} & {} - 2329600s ^ {6} + 3276800с ^ { 7} -2785280s ^ {8} + 1310720s ^ {9} -262144s ^ {10} = {} & 4s (1s) left (5-20s + 16s ^ {2} right) ^ {2} left (1-12s + 16s ^ {2} right) ^ {2} [10pt] S_ {11} (s) = {} & 121s-4840s ^ {2} + 75504s ^ {3} -604032s ^ {4} + 2818816s ^ {5} & {} - 8200192s ^ {6} + 15319040s ^ {7} -18382848s ^ {8} + 13697024s ^ {9} -5767168s ^ {10} + 1048576s ^ {11} = {} & s left (11–220 с. + 1232 с. ^ {2} -2816 с. ^ {3} + 2816 с. ^ {4} -1024 с. ^ {5} right) ^ {2} end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f482dc5a4988b0ea13e6d3e0b90665b0cf30127)







![{ displaystyle { begin {align} Q (AB) & Equiv (B_ {x} -A_ {x}) ^ {2} + (B_ {y} -A_ {y}) ^ {2} & = b ^ {2} + (- a) ^ {2} & = a ^ {2} + b ^ {2} [10pt] Q (BC) & Equiv (C_ {x} -B_ { x}) ^ {2} + (C_ {y} -B_ {y}) ^ {2} & = { bigl (} (b lambda + A_ {x}) - B_ {x} { bigr )} ^ {2} + { bigl (} (- a lambda + A_ {y}) - B_ {y} { bigr)} ^ {2} & = { bigl (} b lambda + (A_ {x} -B_ {x}) { bigr)} ^ {2} + { bigl (} -a lambda + (A_ {y} -B_ {y}) { bigr)} ^ {2 } & = { bigl (} b lambda + (- b) { bigr)} ^ {2} + (- a lambda + a) ^ {2} & = b ^ {2} ( lambda -1) ^ {2} + a ^ {2} (- lambda +1) ^ {2} & = b ^ {2} ( lambda -1) ^ {2} + a ^ {2 } ( lambda -1) ^ {2} & = left (a ^ {2} + b ^ {2} right) ( lambda -1) ^ {2} [10pt] Q (AC ) & Equiv (C_ {x} -A_ {x}) ^ {2} + (C_ {y} -A_ {y}) ^ {2} & = { bigl (} (b lambda + A_ {x}) - A_ {x} { bigr)} ^ {2} + { bigl (} (- a lambda + A_ {y}) - A_ {y} { bigr)} ^ {2} & = (b lambda + A_ {x} -A_ {x}) ^ {2} + (- a lambda + A_ {y} -A_ {y}) ^ {2} & = (b лямбда) ^ {2} + (- a lambda) ^ {2} & = b ^ {2} lambda ^ {2} + (- a) ^ {2} lambda ^ {2} & = b ^ {2} lambda ^ {2} + a ^ {2} lambda ^ {2} & = left (a ^ {2} + b ^ {2} right) lambda ^ {2 } конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9d8c6072c67ff0e08f3ce85aa391ca02ef8834b)
















