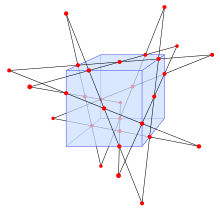
Quadrisecant - Quadrisecant

В геометрия, а четырехугольник или же четырехугольник из изгиб это линия который проходит через четыре точки кривой. Каждая узловая кривая в трехмерном Евклидово пространство имеет квадрискант. Число квадрисекантов алгебраическая кривая в сложное проективное пространство можно вычислить по формуле, полученной с помощью Артур Кэли. Quadrisecants косые линии также связаны с линейчатые поверхности и Шлефли двойная шестерка конфигурация.
В теории узлов
В трехмерном Евклидово пространство, каждый нетривиальный приручить морской узел или же связь имеет квадрискант. Первоначально установлено в случае узловатых полигоны и гладкий узлов Эрика Паннвиц,[1]этот результат был распространен на узлы в подходящем общая позиция и ссылки с ненулевым номер ссылки,[2]а затем и всем нетривиальным ручным узлам и звеньям.[3]
Паннвиц более убедительно доказал, что число различных квадрисекантов ограничено снизу функцией минимального числа граничных особенностей в локально-плоском открытом диске, ограниченном узлом.[1][4] Мортон и Монд (1982) предположил, что количество различных квадрисекантов данного узла всегда не меньше п(п - 1) / 2, где п это номер перехода узла.[2][4] Однако с тех пор были обнаружены контрпримеры к этой гипотезе.[4]
Двухкомпонентные звенья имеют квадрисканты, в которых точки на квадрисканте появляются в чередующемся порядке между двумя компонентами,[2] и нетривиальные узлы имеют квадрицепсы, в которых четыре точки, заказывается циклически в качестве а,б,c,d на узле появляются по порядку а,c,б,d по квадрисканту.[5] Существование этих чередующихся квадрискантов можно использовать для вывода Теорема Фэри-Милнора, а нижняя граница на полная кривизна нетривиального узла.[5] Квадрисканты также использовались для нахождения нижних оценок длина веревки узлов.[6]
В алгебраической геометрии
Артур Кэли вывел формулу для числа квадрисактов алгебраическая кривая в трехмерном сложное проективное пространство, как функция его степень и род.[7] Для кривой степени d и род грамм, количество квадрискантов равно[8]
Косых линий
В трехмерном Евклидово пространство, каждый набор из четырех косые линии в общая позиция либо имеет два квадрисканта (также называемых в этом контексте трансверсали ) или нет. Любые три из четырех линий определяют двояковыпуклая поверхность, в котором один из двух наборов линейчатых линий содержит три заданные линии, а другой линейчатый состоит из трех секущих к заданным линиям. Если четвертая из данных линий проходит через эту поверхность, две точки ее пересечения лежат на двух квадрисскантах; если он не пересекается с поверхностью, то квадрискантов нет.[9]
Квадрисеканты наборов прямых играют важную роль в построении Шлефли двойная шестерка, а конфигурация двенадцати линий, пересекающихся друг с другом в 30 пересечениях. Если пять строк ая (за я = 1,2,3,4,5) даны в трехмерном пространстве, так что все пять пересекаются общей линией б6 но в остальном находятся в общем положении, то каждая из пяти четверок прямых ая имеет второй квадрискант бя, и пять строк бя образованные таким образом все пересекаются общей линией а6. Эти двенадцать линий и 30 точек пересечения аябj образуют двойную шестерку.[10][11]
Рекомендации
- ^ а б Паннвиц, Эрика (1933), "Eine elementargeometrische Eigenschaft von Verschlingungen und Knoten", Mathematische Annalen, 108 (1): 629–672, Дои:10.1007 / BF01452857.
- ^ а б c Мортон, Хью Р .; Монд, Дэвид М.К. (1982), "Замкнутые кривые без квадрискантов", Топология, 21: 235–243, Дои:10.1016/0040-9383(82)90007-6, МИСТЕР 0649756.
- ^ Куперберг, Грег (1994), «Квадрицепсы узлов и звеньев», Журнал теории узлов и ее разветвлений, 3: 41–50, arXiv:математика / 9712205, Дои:10.1142 / S021821659400006X, МИСТЕР 1265452.
- ^ а б c Джин, Гё Тэк (2005), «Квадрицепсы узлов с малым числом пересечений», Физические и численные модели в теории узлов (PDF), Сер. Все узлы, 36, World Sci. Publ., Singapore, стр. 507–523, Дои:10.1142/9789812703460_0025, МИСТЕР 2197955.
- ^ а б Денн, Элизабет Джейн (2004), Чередующиеся квадрицепсы узлов, Кандидат наук. Тезис, Иллинойсский университет в Урбана-Шампейн, arXiv:математика / 0510561, Bibcode:2005математика ..... 10561D.
- ^ Денн, Элизабет; Дяо, Юаньань; Салливан, Джон М. (2006), «Квадрисканты дают новые нижние оценки длины веревки узла», Геометрия и топология, 10: 1–26, arXiv:математика / 0408026, Дои:10.2140 / gt.2006.10.1, МИСТЕР 2207788.
- ^ Кэли, Артур (1863), Философские труды Лондонского королевского общества, 153, стр. 453–483, JSTOR 108806.
- ^ Гриффитс, Филипп; Харрис, Джозеф (2011), Принципы алгебраической геометрии, Библиотека Wiley Classics, 52, John Wiley & Sons, стр. 296, г. ISBN 9781118030776.
- ^ Гильберт, Дэвид; Кон-Фоссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, стр. 164, г. ISBN 978-0-8284-1087-8.
- ^ Шлефли, Людвиг (1858), Кэли, Артур (ред.), «Попытка определить двадцать семь линий на поверхности третьего порядка и вывести такие поверхности в виде видов со ссылкой на реальность линий на поверхности», Ежеквартальный журнал чистой и прикладной математики, 2: 55–65, 110–120.
- ^ Кокстер, Х. С. М. (2006), «Абсолютное свойство четырех касательных друг к другу окружностей», Неевклидовы геометрии, Математика. Appl. (Н. Ю.), 581, Нью-Йорк: Springer, стр. 109–114, Дои:10.1007/0-387-29555-0_5, МИСТЕР 2191243. Кокстер повторяет конструкцию Шлефли и дает несколько ссылок на упрощенные доказательства ее правильности.