Принципы построения сети - Principles of Grid Generation - Wikipedia

Сетки или же сетки представляют собой геометрические формы (сформированные после дискретизации геометрической области), которые представляют собой дискретные ячейки небольшого размера, покрывающие физическую область, цель которых - идентифицировать дискретный объемы или элементы, где законы сохранения может быть применено. У них есть приложения в области вычислительная гидродинамика (CFD), география, проектирование и многие другие места, где численные решения уравнения в частных производных (PDE) обязательны.

Создание числовой сетки - важнейший начальный этап вычислений. числовой решения уравнений, описывающих физический процесс. Точность решение зависит от качества создаваемой сетки. Хорошо построенная сетка может улучшить качество решения, тогда как отклонения от численного решения могут наблюдаться с плохо построенной сеткой.Методы для создания ячейки составляет основу построения сетки. Ниже обсуждаются различные методы построения сетки.

Алгебраические методы

Геометрия сопла

Вычислительная сетка в физическом пространстве

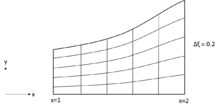
Построение сетки алгебраическими методами основано на математических функция интерполяции. Это делается с использованием известных функций в одном, двух или трех размеры взяв области произвольной формы. Расчетная область может быть не прямоугольной, но для простоты область считается прямоугольной. Основное преимущество методов заключается в том, что они обеспечивают явный контроль физической формы и расстояния сетки. Самая простая процедура, которую можно использовать для создания расчетной сетки, аппроксимирующей границы, - это преобразование нормализации.^[1]
Для сопла с описывающей функцией ${ Displaystyle у = х ^ {2}}$ сетку можно легко сгенерировать с помощью равномерного деления на у-направление с равными интервалами в Икс-направления, которые описываются

{ Displaystyle xi = х ,}

{ displaystyle eta = { frac {y} {y _ { max}}} ,}

куда ${ displaystyle y _ { max}}$ обозначает y-координату стенки сопла. Для заданных значений ( ${ Displaystyle xi}$ , ${ displaystyle eta}$ ) значения ( ${ displaystyle x}$ , ${ displaystyle y}$ ) легко восстанавливается.

Методы дифференциальных уравнений

Подобно алгебраическим методам, дифференциальное уравнение методы также используются для создания сеток. Преимущество использования уравнения в частных производных (PDE) заключается в том, что решение уравнений создания сетки может использоваться для создания сетки. Построение сетки может быть выполнено с использованием всех трех классов уравнения в частных производных.

Эллиптические схемы

Эллиптический PDEs обычно имеют очень плавные решения, ведущие к гладким контурам. Использование его гладкости как преимущества Уравнения Лапласа предпочтительно использовать, потому что Якобиан оказался положительным в результате принципа максимума для гармонические функции. После обширной работы, проделанной Кроули (1962) и Уинслоу (1966)^[2] на PDE путем преобразования физической области в вычислительную плоскость при отображении с использованием Уравнение Пуассона, Томпсон и др. (1974)^[3] много работали над эллиптическими PDEs для создания сеток. В генераторах сетки Пуассона отображение выполняется путем пометки желаемых точек сетки ${ Displaystyle (х, у)}$ на границе физической области с распределением внутренних точек, определяемым путем решения уравнений, записанных ниже

{ Displaystyle xi _ {xx} + xi _ {yy} = P ( xi, eta)}

{ displaystyle eta _ {xx} + eta _ {yy} = Q ( xi, eta)}

куда, ${ Displaystyle ( xi, eta)}$ являются координатами в вычислительной области, а P и Q отвечают за расстояние между точками в D. Преобразование приведенных выше уравнений в вычислительном пространстве дает набор из двух эллиптические уравнения в частных производных формы,

{ displaystyle alpha x _ { xi xi} -2 beta x _ { xi eta} + gamma x _ { eta eta} = - I ^ {2} (Px _ { xi} + Qx _ { eta})}

{ displaystyle alpha y _ { xi xi} -2 beta y _ { xi eta} + gamma y _ { eta eta} = - I ^ {2} (Py _ { xi} + Qy _ { eta})}

куда

{ displaystyle { begin {align} alpha & = x _ { eta} ^ {2} + y _ { eta} ^ {2} beta & = x _ { eta} x _ { xi} + y_ { xi} y _ { eta} gamma & = x _ { xi} ^ {2} + y _ { xi} ^ {2} I & = { frac { delta (x, y)} { delta ( xi, eta)}} = y _ { eta} x _ { xi} -y _ { xi} x _ { eta} end {выровнено}}}

Эти системы уравнений решаются в расчетной плоскости на равномерно распределенной сетке, которая дает нам ${ Displaystyle (х, у)}$ координаты каждой точки в физическом пространстве. Преимущество использования эллиптические уравнения в частных производных является ли связанное с ними решение гладким, а итоговая сетка гладкой. Но спецификация P и Q становится сложной задачей, что добавляет к ее недостаткам. Более того, сетка должна вычисляться после каждого временного шага, что в сумме увеличивает время вычислений.^[4]

Гиперболические схемы

Эта схема генерации сетки обычно применима к задачам с открытыми областями, соответствующими типу PDE описание физической проблемы. Преимущество, связанное с гиперболические PDE заключается в том, что основные уравнения необходимо решить только один раз для создания сетки. Распределение начальных точек вместе с приблизительными граничными условиями формирует требуемый вход, а решение - это продвижение наружу. Стегер и Соренсон (1980)^[5] предложил метод объемной ортогональности, который использует гиперболические уравнения в частных производных для генерации сетки. Для двумерной задачи, учитывая, что вычислительное пространство задается формулой ${ Displaystyle Delta xi = Delta eta = 1}$ , обратное Якобиан дан кем-то,

{ displaystyle x _ { xi} y _ { eta} -x _ { eta} y _ { xi} = I}

куда ${ displaystyle I}$ представляет площадь в физическом пространстве для данной области в вычислительном пространстве. Второе уравнение связывает ортогональность линий сетки на границе в физическом пространстве, которую можно записать как

{ Displaystyle d xi = 0 = xi _ {x} , dx + xi _ {y} , dy.}

За ${ Displaystyle xi}$ и ${ displaystyle eta}$ поверхности должны быть перпендикулярны уравнение принимает вид

{ displaystyle x _ { xi} x _ { eta} + y _ { xi} y _ { eta} = 0.}

Проблема, связанная с такой системой уравнений, заключается в задании ${ displaystyle I}$ . Плохой выбор ${ displaystyle I}$ может привести к сотрясениям и прерывистому распространению этой информации по сетке. Ортогональная сетка генерируется очень быстро, что является преимуществом этого метода.

Параболические схемы

Техника решения аналогична методике гиперболические PDE путем продвижения решения от поверхности начальных данных, удовлетворяющих граничным условиям в конце. Накамура (1982) и Эдвардс (1985) разработали основные идеи создания параболической сетки. Идея использует любой из Лаплас или Уравнение Пуассона и особенно обработка деталей, управляющих эллиптическим поведением. Начальные значения задаются как координаты точки вдоль поверхности ${ displaystyle eta = 0}$ и продвижение решений к внешней поверхности объекта, удовлетворяющего граничным условиям, вдоль ${ Displaystyle xi}$ края.

Контроль шага сетки до сих пор не предлагался. Накамура и Эдвардс, управление сеткой осуществлялось с использованием неравномерного интервала. Генерация параболической сетки демонстрирует преимущество перед генерацией гиперболической сетки в том, что не возникает ударов или разрывов, а сетка является относительно гладкой. Однако определение начальных значений и выбор размера шага для управления точками сетки отнимают много времени, но эти методы могут быть эффективными, когда приобретены знания и опыт.

Вариационные методы

Этот метод включает технику, которая минимизирует сетка гладкость, ортогональность и изменение объема. Этот метод формирует математическую платформу для решения задач построения сетки. В этом методе альтернативная сетка генерируется новым сетка после каждой итерации и вычисления скорости сетки с использованием метод обратной разности. Этот метод является мощным, но его недостатком является необходимость решения уравнений, связанных с сеткой. Требовалась дополнительная работа, чтобы свести к минимуму интегралы что сократит время процессора.

Генерация неструктурированной сетки

Смотрите также Генерация сетки. Основное значение этой схемы состоит в том, что она предоставляет метод, который автоматически генерирует сетку. Используя этот метод, сетки сегментируются на блоки в соответствии с поверхностью элемента, и предоставляется структура для обеспечения соответствующей связи. Интерпретировать данные поток решатель. Когда используется неструктурированная схема, основной интерес состоит в том, чтобы удовлетворить потребности пользователя, и для выполнения этой задачи используется генератор сети. Хранение информации в структурированной схеме клетка в ячейку вместо сетки в сетку и, следовательно, требуется больше места в памяти. Из-за случайного расположения ячеек решатель эффективность в неструктурированной - меньше по сравнению со структурированной схемой.^[6]

Некоторые моменты необходимо учитывать во время построения сетки. строительство. Точка сетки с высоким разрешением создает трудности как для структурированных, так и для неструктурированных изображений. Например, в случае пограничный слой структурированная схема дает вытянутую сетку по направлению потока. С другой стороны, для неструктурированных сеток требуется более высокая ячейка. плотность в пограничном слое, потому что ячейка должна быть как равносторонний по возможности избежать ошибок.^[7]

Информация о подключении

Мы должны определить, какая информация требуется для идентификации ячейки и всех соседей ячейки в вычислительный сетка. Мы можем выбрать расположение произвольный точки в любом месте для неструктурированной сетки. Схема вставки точек используется для независимой вставки точек и определения связности ячеек. Это предполагает, что точки будут идентифицированы по мере их вставки. Логика для установления нового соединения определяется после вставки точек. Необходимы данные, образующие точку сетки, которая определяет ячейку сетки. По мере формирования каждой ячейки она нумеруется и точки сортируются. Кроме того, необходима информация о соседних сотах.

Адаптивная сетка

Проблема в решении уравнения в частных производных Использование предыдущих методов состоит в том, что сетка строится, а точки распределяются в физической области до того, как станут известны детали решения. Таким образом, сетка может или не может быть лучшей для данной проблемы.^[8]

Адаптивные методы используются для улучшения точность решений. Адаптивный метод называется методом «h», если используется уточнение сетки, методом «r», если количество точек сетки фиксировано и не перераспределяется, и «p», если порядок схемы решения увеличивается в теории конечных элементов. Многомерные задачи с использованием схемы эквираспределения могут быть решены несколькими способами. Самыми простыми для понимания являются генераторы сетки Пуассона с функцией управления, основанной на равнораспределении весовой функции с распространение задается кратным желаемому объему ячейки. Схема равнораспределения также может быть применена к неструктурированной задаче. Проблема заключается в том, что при очень большом перемещении точки сетки затрудняется подключение.

Постоянный поток и точный по времени расчет расхода может быть решен с помощью этого адаптивного метода. Сетка уточняется и после заранее определенного количества итераций, чтобы адаптировать ее к задаче устойчивого потока. Сетка перестанет подстраиваться под изменения, как только решение сойдется. Вовремя точная связь корпуса уравнения в частных производных физической задачи и описывающих движение сетки.