Теорема Морли о трехсекторах - Morleys trisector theorem - Wikipedia

В плоская геометрия, Теорема морли о трехсекторах заявляет, что в любом треугольник, три точки пересечения соседних трисектора углов для мужчин равносторонний треугольник, называется первый треугольник Морли или просто Треугольник Морли. Теорема была открыта в 1899 г. Англо-американский математик Фрэнк Морли. Имеет различные обобщения; в частности, если все трисектора пересекаются, получается четыре других равносторонних треугольника.
Доказательства
Есть много доказательства теоремы Морли, некоторые из которых очень технические.[1] Несколько ранних доказательств основывались на деликатных тригонометрический расчеты. Недавние доказательства включают алгебраический доказательство Ален Конн (1998, 2004 ) распространяя теорему на общие поля кроме характеристики три, и Джон Конвей Доказательство элементарной геометрии.[2][3] Последний начинается с равностороннего треугольника и показывает, что вокруг него можно построить треугольник, который будет похожий в любой выбранный треугольник. Теорема Морли не выполняется в сферический[4] и гиперболическая геометрия.
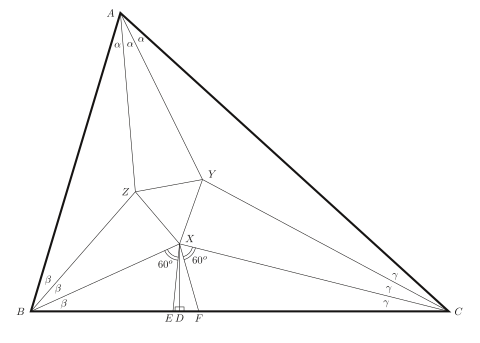
Одно доказательство использует тригонометрическое тождество
(1)
который, используя тождество суммы двух углов, можно показать, что он равен
Последнее уравнение можно проверить, дважды применив тождество суммы двух углов к левой части и исключив косинус.
Точки построены на как показано. У нас есть , сумма углов любого треугольника, поэтому Следовательно, углы треугольника находятся и
С рисунка
(2)
и
(3)
Также из рисунка
и
(4)
Закон синусов применительно к треугольникам и дает
(5)
и
(6)
Выразите высоту треугольника двумя способами
и
где уравнение (1) использовалось для замены и в этих двух уравнениях. Подставляя уравнения (2) и (5) в уравнение и уравнения (3) и (6) в уравнение дает
и
Поскольку числители равны
или же
Поскольку угол и угол равны и стороны, образующие эти углы, находятся в одинаковом соотношении, треугольники и похожи.
Подобные углы и равный , и подобные углы и равный Подобные аргументы дают базовые углы треугольников и
В частности угол оказывается и из рисунка мы видим, что
Подстановка урожайности
где уравнение (4) использовалось для угла и поэтому
Аналогично остальные углы треугольника оказываются
Сторона и площадь
У первого треугольника Морли длины сторон[5]
куда р это по окружности исходного треугольника и А, Б, и C - углы исходного треугольника. Поскольку площадь равностороннего треугольника площадь треугольника Морли можно выразить как
Треугольники Морли
Теорема Морли влечет за собой 18 равносторонних треугольников. Треугольник, описанный в приведенной выше теореме о трисекторах, называется первый треугольник Морли, имеет вершины, заданные в трилинейные координаты относительно треугольника ABC следующее:
- А-vertex = 1: 2 cos (C/ 3): 2 cos (B/3)
- B-vertex = 2 cos (C/ 3): 1: 2 cos (А/3)
- C-vertex = 2 cos (B/ 3): 2 cos (А/3) : 1
Другой равносторонний треугольник Морли, который также является центральным, называется треугольником. второй треугольник Морли и задается этими вершинами:
- А-вершина = 1: 2 cos (C/ 3 - 2π / 3): 2 cos (B/ 3 - 2π / 3)
- B-вершина = 2 cos (C/ 3 - 2π / 3): 1: 2 cos (А/ 3 - 2π / 3)
- C-вершина = 2 cos (B/ 3 - 2π / 3): 2 cos (А/ 3 - 2π / 3): 1
Третий из 18 равносторонних треугольников Морли, который также является центральным треугольником, называется третий треугольник Морли и задается этими вершинами:
- А-vertex = 1: 2 cos (C/ 3 - 4π / 3): 2 cos (B/ 3 - 4π / 3)
- B-vertex = 2 cos (C/ 3 - 4π / 3): 1: 2 cos (А/ 3 - 4π / 3)
- C-vertex = 2 cos (B/ 3 - 4π / 3): 2 cos (А/ 3 - 4π / 3): 1
Первый, второй и третий треугольники Морли попарно гомотетичный. Еще один гомотетический треугольник образован тремя точками Икс на описанной окружности треугольника ABC на которой линия XX −1 касается описанной окружности, где Икс −1 обозначает изогональный конъюгат из Икс. Этот равносторонний треугольник, называемый окружной треугольник, имеет эти вершины:
- А-вершина = csc (C/3 − B/ 3): csc (B/3 + 2C/ 3): −csc (C/3 + 2B/3)
- B-вершина = −csc (А/3 + 2C/ 3): csc (А/ 3 - С / 3): csc (C/3 + 2А/3)
- C-вершина = csc (А/3 + 2B/ 3): −csc (B/3 + 2А/ 3): csc (B/3 − А/3)
Пятый равносторонний треугольник, также гомотетичный остальным, получается вращением касательного треугольника π / 6 вокруг его центра. Называется околонормальный треугольник, его вершины следующие:
- А-вершина = сек (C/3 − B/ 3): −сек (B/3 + 2C/ 3): −сек (C/3 + 2B/3)
- B-вершина = −сек (А/3 + 2C/ 3): сек (А/3 − C/ 3): −сек (C/3 + 2А/3)
- C-вершина = −сек (А/3 + 2B/ 3): −сек (B/3 + 2А/ 3): сек (B/3 − А/3)
Операция под названием «экстраверсия» может использоваться для получения одного из 18 треугольников Морли из другого. Каждый треугольник можно экстравертировать тремя способами; 18 треугольников Морли и 27 экстравертных пар треугольников образуют 18 вершин и 27 ребер График Паппа.[6]
Связанные центры треугольников
В центроид первого треугольника Морли приведен в трилинейные координаты к
- Центр Морли = Икс(356) = соз (А/ 3) + 2 cos (B/ 3) cos (C/ 3): cos (B/ 3) + 2 cos (C/ 3) cos (А/ 3): cos (C/ 3) + 2 cos (А/ 3) cos (B/3).
Первый треугольник Морли - это перспектива в треугольник ABC:[7] линии, каждая из которых соединяет вершину исходного треугольника с противоположной вершиной треугольника Морли соглашаться в момент
- 1-й центр Морли-Тейлора-Марра = Икс(357) = сек (А/ 3): сек (B/ 3): сек (C/3).
Смотрите также
Примечания
- ^ Богомольный Александр, Чудо Морли, Разрезать узел, получено 2010-01-02
- ^ Доказательство Дж. Конвея, из Богомольного.
- ^ Конвей, Джон (2006), «Сила математики», в Блэквелле, Алан; Маккей, Дэвид (ред.), Мощность (PDF), Cambridge University Press, стр. 36–50, ISBN 978-0-521-82377-7, получено 2010-10-08
- ^ Теорема Морли в сферической геометрии, Java-апплет.
- ^ Вайсштейн, Эрик В. «Первый треугольник Морли». Материал из MathWorld - веб-ресурса Wolfram. [1]
- ^ Парень (2007).
- ^ Fox, M.D .; и Гоггинс, Дж. Р. "Обобщенная диаграмма Морли", Математический вестник 87, ноябрь 2003 г., 453–467.
Рекомендации
- Конн, Ален (1998), «Новое доказательство теоремы Морли», Публикации Mathématiques de l'IHÉS, S88: 43–46.
- Конн, Ален (Декабрь 2004 г.), «Симметрии» (PDF), Европейское математическое общество Новостная рассылка, 54.
- Кокстер, Х. С. М.; Грейцер, С. Л. (1967), Возвращение к геометрии, Математическая ассоциация Америки, LCCN 67-20607
- Фрэнсис, Ричард Л. (2002), «Вехи современной математики: загадка Морли» (PDF), Журнал математических наук штата Миссури, 14 (1).
- Гай, Ричард К. (2007), «Теорема о маяке, Морли и Малфатти - бюджет парадоксов» (PDF), Американский математический ежемесячный журнал, 114 (2): 97–141, JSTOR 27642143, МИСТЕР 2290364, заархивировано из оригинал (PDF) на 2010-04-01.
- Oakley, C.O .; Бейкер, Дж. К. (1978), "Теорема о трехсекторах Морли", Американский математический ежемесячный журнал, 85 (9): 737–745, Дои:10.2307/2321680, JSTOR 2321680.
- Тейлор, Ф. Гланвилл; Марр, У. Л. (1913–14), «Шесть трисектрис каждого из углов треугольника», Труды Эдинбургского математического общества, 33: 119–131.
внешняя ссылка
- Теорема Морли в MathWorld
- Теорема Морли о трисекции на MathPages
- Теорема Морли Александр Павлик, Демонстрационный проект Wolfram.















































