Расстояние Фреше - Fréchet distance

В математике Расстояние Фреше это мера сходства между кривые который учитывает расположение и порядок точек вдоль кривых. Он назван в честь Морис Фреше.

Интуитивное определение

Представьте себе человека, идущего по конечной изогнутой дорожке, выгуливая свою собаку на поводке, при этом собака проходит отдельный конечный изогнутый путь. Каждый может изменять свою скорость, чтобы поводок оставался слабым, но ни один из них не может двигаться назад. Расстояние Фреше между двумя изгибами - это длина самого короткого поводка, достаточная для того, чтобы оба могли пройти свои отдельные пути от начала до конца. Обратите внимание, что определение симметрично относительно двух кривых - расстояние Фреше было бы таким же, если бы собака выгуливала своего хозяина.

Формальное определение

Позволять ${displaystyle S}$ быть метрическое пространство. А изгиб ${displaystyle A}$ в ${displaystyle S}$ это непрерывный карта от единичный интервал в ${displaystyle S}$ , т.е. ${displaystyle A: [0,1] ightarrow S}$ . А повторная параметризация ${displaystyle alpha}$ из ${displaystyle [0,1]}$ является непрерывным, неубывающий, сюрприз ${displaystyle alpha: [0,1] ightarrow [0,1]}$ .

Позволять ${displaystyle A}$ и ${displaystyle B}$ быть двумя заданными кривыми в ${displaystyle S}$ . Затем Расстояние Фреше между ${displaystyle A}$ и ${displaystyle B}$ определяется как инфимум по всем параметризациям ${displaystyle alpha}$ и ${displaystyle eta}$ из ${displaystyle [0,1]}$ максимума по всем ${displaystyle tin [0,1]}$ расстояния в ${displaystyle S}$ между ${displaystyle A (alpha (t))}$ и ${displaystyle B (eta (t))}$ . В математических обозначениях расстояние Фреше ${displaystyle F (A, B)}$ является

${displaystyle F (A, B) = inf _ {alpha, eta} ,, max _ {tin [0,1]} ,, {Bigg {} d {Big (} A (alpha (t)) ,, B ( eta (t)) {Big)} {Bigg}}}$

куда ${displaystyle d}$ это функция расстояния из ${displaystyle S}$ .

Неформально мы можем думать о параметре ${displaystyle t}$ как «время». Потом, ${displaystyle A (alpha (t))}$ позиция собаки и ${displaystyle B (eta (t))}$ положение хозяина собаки во время ${displaystyle t}$ (или наоборот). Длина поводка между ними во времени ${displaystyle t}$ это расстояние между ${displaystyle A (alpha (t))}$ и ${displaystyle B (eta (t))}$ . Взяв точную нижнюю грань по всем возможным перепараметризациям ${displaystyle [0,1]}$ соответствует выбору прогулки по заданным дорожкам, при которой максимальная длина поводка минимальна. Ограничение, что ${displaystyle alpha}$ и ${displaystyle eta}$ быть неубывающим означает, что ни собака, ни ее владелец не могут отступить.

Метрика Фреше учитывает поток двух кривых, потому что пары точек, расстояние которых влияет на расстояние Фреше, непрерывно перемещаются вдоль своих соответствующих кривых. Это делает расстояние Фреше лучшей мерой сходства кривых, чем альтернативы, такие как Расстояние Хаусдорфа, для произвольных точечных множеств. Две кривые могут иметь небольшое расстояние Хаусдорфа, но большое расстояние Фреше.

Расстояние Фреше и его варианты находят применение в нескольких задачах, начиная с морфинг^[1] и распознавание почерка^[2] к выравнивание структуры белка.^[3] Альт и Годау^[4] были первыми, кто описал алгоритм с полиномиальным временем для вычисления расстояния Фреше между двумя полигональные кривые в Евклидово пространство, основанный на принципе параметрический поиск. Время работы их алгоритма ${displaystyle O (журнал mncdot (мин))}$ для двух ломаных с м и п сегменты.

Диаграмма свободного пространства

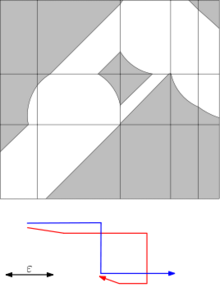
пример диаграммы свободного пространства

Диаграмма свободного пространства красной и синей кривой. В отличие от определения в тексте, где для обеих кривых используется интервал параметра [0,1], в этом примере кривые параметризуются длиной дуги.

Важным инструментом для вычисления расстояния Фреше двух кривых является диаграмма свободного пространства, введенная Альт и Годо.^[4]Диаграмма свободного пространства между двумя кривыми для заданного порогового значения расстояния ε представляет собой двумерную область в пространстве параметров, которая состоит из всех пар точек на двух кривых на расстоянии не более ε:

${displaystyle D_ {varepsilon} (A, B): = {, (alpha, eta) in [0,1] ^ {2} mid d (A (alpha), B (eta)) leq varepsilon,}}$

Расстояние Фреше ${displaystyle F (A, B)}$ не превосходит ε тогда и только тогда, когда диаграмма свободного пространства ${displaystyle D_ {varepsilon} (A, B)}$ содержит путь от левого нижнего угла к правому верхнему углу, который монотонен как в горизонтальном, так и в вертикальном направлении.

Как расстояние между распределениями вероятностей (оценка FID)

Помимо измерения расстояний между кривыми, расстояние Фреше также можно использовать для измерения разницы между распределения вероятностей. Для двух многомерных гауссовских распределений со средними ${displaystyle mu _ {X}}$ и ${displaystyle mu _ {Y}}$ и ковариационные матрицы ${displaystyle Sigma _ {X}}$ и ${displaystyle Sigma _ {Y}}$ , расстояние Фреше между этими распределениями равно^[5]

${displaystyle d ^ {2} = | mu _ {X} -mu _ {Y} | ^ {2} + tr (Sigma _ {X} + Sigma _ {Y} -2 (Sigma _ {X} Sigma _ { Y}) ^ {1/2})}$ .

Это расстояние является основой для Начальная дистанция Фреше (FID), который используется для сравнения изображений, созданных порождающая состязательная сеть с реальными изображениями, которые использовались для обучения.

Варианты

В слабое расстояние Фреше является вариантом классической дистанции Фреше без требования, чтобы конечные точки двигались монотонно вдоль соответствующих изгибов - собаке и ее владельцу разрешается отступать, чтобы поводок между ними оставался коротким. Альт и Годау^[4] описать более простой алгоритм вычисления слабого расстояния Фреше между многоугольными кривыми, основанный на вычислении минимаксные пути в ассоциированном сеточный график.

В дискретное расстояние Фреше, также называемый расстояние сцепления, является приближением метрики Фреше для ломаных кривых, определенной Эйтером и Маннилой.^[6] Дискретное расстояние Фреше учитывает только положения поводка, когда его концы расположены в вершинах двух многоугольных кривых, но никогда не внутри края. Эта специальная структура позволяет вычислять дискретное расстояние Фреше за полиномиальное время с помощью простого алгоритма динамического программирования.

Когда две кривые вложены в метрическое пространство, отличное от евклидова, например многогранный рельеф или какое-то евклидово пространство с препятствиями, расстояние между двумя точками на кривых наиболее естественно определяется как длина кратчайший путь между ними. Поводок должен быть геодезический присоединение к его конечным точкам. Результирующая метрика между кривыми называется метрикой геодезическое расстояние Фреше.^[1]^[7]^[8] Готовить и Венк^[7] описать алгоритм с полиномиальным временем для вычисления геодезического расстояния Фреше между двумя многоугольными кривыми в простой многоугольник.

Если мы дополнительно потребуем, чтобы поводок непрерывно перемещался в окружающем метрическом пространстве, то мы получим понятие гомотопическое расстояние Фреше^[9] между двумя кривыми. Поводок не может прерывисто переключаться из одного положения в другое - в частности, поводок не может перепрыгивать через препятствия и может проноситься через гору на местности, только если он достаточно длинный. Движение поводка описывает гомотопия между двумя кривыми. Камеры и другие.^[9] описать алгоритм с полиномиальным временем для вычисления гомотопического расстояния Фреше между многоугольными кривыми в евклидовой плоскости с препятствиями.

Примеры

Расстояние Фреше между двумя концентрическими окружностями радиуса ${displaystyle r_ {1}}$ и ${displaystyle r_ {2}}$ соответственно ${displaystyle | r_ {1} -r_ {2} |.}$ Самый длинный поводок требуется, когда хозяин стоит на месте, а собака движется на противоположную сторону круга ( ${displaystyle r_ {1} + r_ {2}}$ ), и самый короткий поводок, когда и владелец, и собака ходят с постоянной угловой скоростью по окружности ( ${displaystyle | r_ {1} -r_ {2} |}$ ).

дальнейшее чтение

де Берг, Марк, "Анализ траекторий движущихся объектов", Вычислительная геометрия, две избранные темы (PDF), стр. 11–75.
Аронов Борис; Хар-Пелед, Сариэль; Кнауэр, Кристиан; Ван, Юсу; Венк, Карола (2006), "Расстояние Фреше для кривых, повторное посещение", Proc. 14-й Европейский симпозиум по алгоритмам (PDF), Конспект лекций по информатике, 4168, Springer-Verlag, стр. 52–63, arXiv:1504.07685, Дои:10.1007/11841036_8, заархивировано из оригинал (PDF) на 2010-06-12.
Альт, Гельмут; Бучин, Майке (2010), «Можем ли мы вычислить сходство между поверхностями?», Дискретная и вычислительная геометрия, 43: 78–99, arXiv:cs.CG/0703011, Дои:10.1007 / s00454-009-9152-8.

[efrat02new-1] а ^б Эфрат, Алон; Гибас, Леонидас Дж.; Хар-Пелед, Сариэль; Митчелл, Джозеф С. Б.; Мурали, Т. М. (2002), «Новые меры сходства между полилиниями с приложениями для морфинга и перемещения полигонов» (PDF), Дискретная и вычислительная геометрия, 28 (4): 535–569, Дои:10.1007 / s00454-002-2886-1.

[sri07frechet-2] Sriraghavendra, R .; Karthik, K .; Бхаттачарья, Чиранджиб (2007 г.), «Подход на основе расстояния Фреше для поиска рукописных документов в Интернете», Proc. 9-я Международная конференция по анализу и распознаванию документов (ICDAR '07), стр. 461–465, Дои:10.1109 / ICDAR.2007.121.

[minghui08protein-3] Минхуэй, Цзян; Инь, Сюй; Биньхай, Чжу (2008), «Выравнивание структуры-структуры белка с дискретным расстоянием Фреше» (PDF), Журнал биоинформатики и вычислительной биологии, 6 (1): 51–64, Дои:10.1142 / S0219720008003278, PMID 18324745.

[alt95frechet-4] а ^б ^c Альт, Гельмут; Годау, Майкл (1995), «Вычисление расстояния Фреше между двумя многоугольными кривыми» (PDF), Международный журнал вычислительной геометрии и приложений, 5 (1–2): 75–91, Дои:10.1142 / S0218195995000064.

[gaussian-5] Доусон, Д. С.; Ландау Б.В. (1 сентября 1982 г.). «Расстояние Фреше между многомерными нормальными распределениями». Журнал многомерного анализа. 12 (3): 450–455. Дои:10.1016 / 0047-259X (82) 90077-X. ISSN 0047-259X.

[eiter94discrete-6] Эйтер, Томас; Маннила, Хейкки (1994), Вычисление дискретного расстояния Фреше (PDF), Тех. Отчет CD-TR 94/64, Лаборатория экспертных систем Христиана Доплера, Технический университет Вены, Австрия.

[cook08geodesic-7] а ^б Кук, Атлас Ф., IV; Венк, Карола (2008), Геодезическая дистанция Фреше с полигональными препятствиями (PDF), Тех. Отчет CS-TR-2008-0010, Техасский университет в Сан-Антонио.

[maheshwari05frechet-8] Махешвари, Анил; Йи, Цзехуа (2005), "О вычислении расстояния Фреше двух путей на выпуклом многограннике", Proc. 21-й Европейский семинар по вычислительной геометрии (PDF), стр. 41–44.

[chambers09homotopic-9] а ^б Чемберс, Эрин Вульф; Колен де Вердьер, Эрик; Эриксон, Джефф; Лазар, Сильвен; Лазарь, Франциск; Тайт, Шрипад (2009), «Гомотопическое расстояние Фреше между кривыми, или Прогулка с собакой в лесу за полиномиальное время» (PDF), Вычислительная геометрия: теория и приложения, 43 (3): 295–311, Дои:10.1016 / j.comgeo.2009.02.008.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]