Набор Delone - Delone set
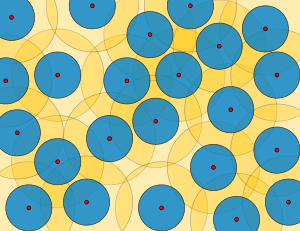
В математической теории метрические пространства, ε-сети, ε-упаковки, ε-покрытия, равномерно дискретные множества, относительно плотные множества, и Наборы Delone (названный в честь Борис Делоне ) являются несколькими тесно связанными определениями хорошо разнесенных наборов точек, а радиус упаковки и радиус покрытия из этих наборов измеряют, насколько хорошо они расположены. Эти наборы находят применение в теория кодирования, аппроксимационные алгоритмы, и теория квазикристаллы.
Определения
Если (M,d) - метрическое пространство, а Икс это подмножество M, то радиус упаковки из Икс половина инфимум расстояний между отдельными членами Икс. Если радиус упаковки р, то откройте шары радиуса р с центром в точках Икс все будут не пересекаться друг с другом, и каждый открытый шар с центром в одной из точек Икс с радиусом 2р будет отделен от остальной части Икс. В радиус покрытия из Икс это нижняя грань чисел р так что каждая точка M находится на расстоянии р не менее одной точки в Икс; то есть это наименьший радиус, при котором замкнутые шары этого радиуса с центрами в точках Икс есть все M как их союз. An ε-упаковка это набор Икс радиуса упаковки ≥ε/ 2 (эквивалентно минимальное расстояние ≥ ε), ε-покрытие это набор Икс радиуса покрытия ≤ε, и ε-сеть это набор, который одновременно является ε-упаковка и ε-покрытие. Набор есть равномерно дискретный если он имеет ненулевой радиус упаковки, и относительно плотный если он имеет конечный радиус покрытия. А Набор Delone - множество, которое одновременно является равномерно дискретным и относительно плотным; таким образом, каждый ε-net - это Делоне, но не наоборот.[1][2]
Построение ε-сетей
Как наиболее ограничительное из приведенных выше определений, ε-сети, по крайней мере, так же сложно построить, как ε-упаковки, ε-покрытия и множества Делоне. Однако всякий раз, когда точки M есть хороший порядок, трансфинитная индукция показывает, что можно построить ε-сеть N, включив в N каждая точка, для которой нижняя грань расстояний до множества более ранних точек в упорядочении не меньше ε. Для конечных наборов точек в евклидовом пространстве ограниченной размерности каждая точка может быть проверена за постоянное время, отображая ее на сетку ячеек диаметра ε и используя хеш-таблица чтобы проверить, какие соседние ячейки уже содержат точки N; таким образом, в этом случае ε-сеть может быть построена в линейное время.[3][4]
Для более общих конечных или компактный метрических пространств, альтернативный алгоритм Тео Гонсалес на основе самый дальний обход можно использовать для построения конечной ε-сети. Этот алгоритм инициализирует сеть N быть пустым, а затем многократно добавляет к N самая дальняя точка в M из N, произвольно разрывая связи и останавливаясь, когда все точкиM находятся на расстоянии ε отN.[5] В пространства ограниченной удвоенной размерности, Алгоритм Гонсалеса может быть реализован за O (п бревноп) время для наборов точек с полиномиальным соотношением между их самым дальним и самым близким расстояниями и аппроксимировано за ту же границу времени для произвольных наборов точек.[6]
Приложения
Теория кодирования
В теории коды с исправлением ошибок, метрическое пространство, содержащее код блока C состоит из строк фиксированной длины, например п, взятый за алфавит размера q (можно рассматривать как векторов ), с Метрика Хэмминга. Это пространство обозначается . Радиус покрытия и радиус упаковки этого метрического пространства связаны со способностью кода исправлять ошибки.
Алгоритмы аппроксимации
Хар-Пелед и Райхель (2013) описывают алгоритмическую парадигму, которую они называют «чистить и сокращать» для проектирования аппроксимационные алгоритмы для некоторых типов задач геометрической оптимизации, определенных на множествах точек в Евклидовы пространства. Алгоритм этого типа работает, выполняя следующие шаги:
- Выберите случайную точку п из набора точек найти ближайшего соседа q, а ε - расстояние между п и q.
- Проверить, является ли ε (приблизительно) больше или меньше оптимального значения решения (используя метод, специфичный для конкретной решаемой задачи оптимизации)
- Если он больше, удалите из ввода точки, ближайший сосед которых находится дальше, чем ε
- Если он меньше, построить ε-сеть N, и удалите из ввода точки, которых нет в N.
В обоих случаях ожидаемое количество оставшихся точек уменьшается на постоянный коэффициент, поэтому во времени доминирует этап тестирования. Как они показывают, эту парадигму можно использовать для построения алгоритмов быстрого приближения для k-центр кластеризация, поиск пары точек со средним расстоянием и несколько связанных проблем.
Иерархическая система сетей, называемая сетевое дерево, может использоваться в пространства ограниченной удвоенной размерности строить хорошо разделенные парные разложения, геометрические ключи, и приблизительный ближайшие соседи.[6][7]
Кристаллография
Для очков в Евклидово пространство, множество Икс это Набор Мейера если он относительно плотный и его набор различий Икс − Икс равномерно дискретна. Эквивалентно, Икс является множеством Мейера, если оба Икс и Икс − Икс делоне. Наборы Мейера названы в честь Ив Мейер, кто их представил (с другим, но эквивалентным определением, основанным на гармонический анализ ) как математическая модель для квазикристаллы. Они включают точечные наборы решетки, Мозаики Пенроуза, а Суммы Минковского этих множеств с конечными множествами.[8]
В Клетки Вороного симметричных множеств Делоне образуют многогранники, заполняющие пространство называется плезиоэдры.[9]
Смотрите также
Рекомендации
- ^ Кларксон, Кеннет Л. (2006), «Построение триангуляции с использованием ε-сетки ", STOC'06: Материалы 38-го ежегодного симпозиума ACM по теории вычислений, Нью-Йорк: ACM, стр. 326–335, Дои:10.1145/1132516.1132564, ISBN 1595931341, МИСТЕР 2277158.
- ^ В некоторых источниках используется "ε-net "для того, что здесь называется"ε- покрытие "; см., например, Сазерленд, У.А. (1975), Введение в метрические и топологические пространства, Oxford University Press, стр. 110, ISBN 0-19-853161-3, Zbl 0304.54002.
- ^ Хар-Пелед, С. (2004), "Движение кластеров", Дискретная и вычислительная геометрия, 31 (4): 545–565, Дои:10.1007 / s00454-004-2822-7, МИСТЕР 2053498.
- ^ Хар-Пелед, С .; Райчел Б. (2013), "Сеть и обрезка: алгоритм линейного времени для задач Евклидова расстояния", STOC'13: Материалы 45-го ежегодного симпозиума ACM по теории вычислений, стр. 605–614, arXiv:1409.7425.
- ^ Гонсалес, Т. Ф. (1985), "Кластеризация для минимизации максимального межкластерного расстояния", Теоретическая информатика, 38 (2–3): 293–306, Дои:10.1016/0304-3975(85)90224-5, МИСТЕР 0807927.
- ^ а б Хар-Пелед, С .; Мендель, М. (2006), "Быстрое построение сетей в низкоразмерных метриках и их приложения", SIAM Журнал по вычислениям, 35 (5): 1148–1184, arXiv:cs / 0409057, Дои:10.1137 / S0097539704446281, МИСТЕР 2217141.
- ^ Krauthgamer, Роберт; Ли, Джеймс Р. (2004), «Навигация в сетях: простые алгоритмы поиска по близости», Материалы 15-го ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA '04), Филадельфия, Пенсильвания, США: Общество промышленной и прикладной математики, стр. 798–807, ISBN 0-89871-558-X.
- ^ Муди, Роберт В. (1997), «Множества Мейера и их двойники», Математика дальнего апериодического порядка (Waterloo, ON, 1995), Институты перспективных наук НАТО, серия C: математические и физические науки, 489, Dordrecht: Kluwer Academic Publishers, стр. 403–441, МИСТЕР 1460032.
- ^ Грюнбаум, Бранко; Шепард, Г.С. (1980), «Плитки с конгруэнтными плитками», Бюллетень Американского математического общества, Новая серия, 3 (3): 951–973, Дои:10.1090 / S0273-0979-1980-14827-2, МИСТЕР 0585178.
внешняя ссылка
- Набор Delone - Энциклопедия Tilings

