Теорема Берри – Эссеена - Berry–Esseen theorem

В теория вероятности, то Центральная предельная теорема заявляет, что при определенных обстоятельствах распределение вероятностей масштабных среднее значение случайной выборки сходится к нормальное распределение при увеличении размера выборки до бесконечности. При более сильных предположениях Теорема Берри – Эссеена, или же Неравенство Берри – Эссеена, дает более количественный результат, потому что он также определяет скорость, с которой имеет место эта сходимость, давая оценку максимальной ошибки приближение между нормальным распределением и истинным распределением масштабированного выборочного среднего. Приближение измеряется Расстояние Колмогорова – Смирнова. В случае независимые образцы, скорость сходимости п^−1/2, куда п - размер выборки, а константа оценивается через в третьих абсолютный нормализованные моменты.

Формулировка теоремы

Формулировки теоремы различаются, так как она была независимо открыта двумя математики, Эндрю С. Берри (в 1941 г.) и Карл-Густав Эссеен (1942), которые затем вместе с другими авторами неоднократно уточняли его в последующие десятилетия.

Одинаково распределенные слагаемые

Одна из версий, несколько жертвуя общностью ради ясности, заключается в следующем:

Существует положительный постоянный C так что если Икс₁, Икс₂, ..., находятся i.i.d. случайные переменные с E (Икс₁) = 0, E (Икс₁²) = σ² > 0 и E (|Икс₁|³) = ρ <∞,^{[примечание 1]} и если мы определим

${ displaystyle Y_ {n} = {X_ {1} + X_ {2} + cdots + X_ {n} over n}}$

в выборочное среднее, с F_п в кумулятивная функция распределения из

${ displaystyle {Y_ {n} { sqrt {n}} over { sigma}},}$

и Φ - кумулятивная функция распределения стандартное нормальное распределение, то для всех Икс и п,

${ displaystyle left | F_ {n} (x) - Phi (x) right | leq {C rho over sigma ^ {3} { sqrt {n}}}. ( 1)}$

Иллюстрация различия кумулятивных функций распределения, упомянутых в теореме.

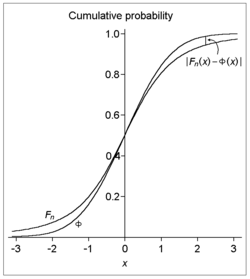
То есть: учитывая последовательность независимые и одинаково распределенные случайные величины, каждый из которых иметь в виду нулевой и положительный отклонение, если дополнительно третий абсолют момент конечно, то кумулятивные функции распределения из стандартизированный среднее выборочное и стандартное нормальное распределение различаются (по вертикали, на графике) не более чем на заданную величину. Обратите внимание, что ошибка аппроксимации для всех п (и, следовательно, предельная скорость сходимости для неопределенных п достаточно большой) ограничен порядок из п^−1/2.

Расчетные значения константы C значительно снизились с годами, с первоначального значения 7,59 на Эссеен (1942), до 0,7882 на ван Бик (1972), затем 0.7655 по Шиганов (1986), затем 0.7056 по Шевцова (2007), затем 0.7005 по Шевцова (2008), затем 0.5894 по Тюрин (2009), затем 0.5129 по Королев и Шевцова (2010а), затем 0.4785 по Тюрин (2010). Подробный обзор можно найти в статьях. Королев и Шевцова (2010а) и Королев и Шевцова (2010b). Лучшая оценка на 2012 год^{[Обновить]}, C <0,4748, следует из неравенства

${ Displaystyle sup _ {х in mathbb {R}} left | F_ {n} (x) - Phi (x) right | leq {0,33554 ( rho +0,415 sigma ^ {3} ) over sigma ^ {3} { sqrt {n}}},}$

из-за Шевцова (2011), поскольку σ³ ≤ ρ и 0,33554 · 1,415 <0,4748. Однако если ρ ≥ 1.286σ³, то оценка

${ displaystyle sup _ {x in mathbb {R}} left | F_ {n} (x) - Phi (x) right | leq {0,3328 ( rho +0,429 sigma ^ {3} ) over sigma ^ {3} { sqrt {n}}},}$

что также доказано в Шевцова (2011), дает еще более точную верхнюю оценку.

Эссеен (1956) доказал, что константа также удовлетворяет нижней оценке

${ displaystyle C geq { frac {{ sqrt {10}} + 3} {6 { sqrt {2 pi}}}} приблизительно 0,40973 приблизительно { frac {1} { sqrt {2 pi}}} + 0,01079.}$

Неоднозначно распределенные слагаемые

Позволять Икс₁, Икс₂, ..., быть независимыми случайными величинами с E (Икс_я) = 0, E (Икс_я²) = σ_я² > 0 и E (|Икс_я|³) = ρ_я <∞. Кроме того, пусть

${ Displaystyle S_ {n} = {X_ {1} + X_ {2} + cdots + X_ {n} over { sqrt { sigma _ {1} ^ {2} + sigma _ {2} ^ {2} + cdots + sigma _ {n} ^ {2}}}}}$

быть нормализованным п-я частичная сумма. Обозначить F_п в cdf из S_п, а Φ cdf стандартное нормальное распределение. Для удобства обозначим

${ displaystyle { vec { sigma}} = ( sigma _ {1}, ldots, sigma _ {n}), { vec { rho}} = ( rho _ {1}, ldots, rho _ {n}).}$

В 1941 г. Эндрю С. Берри доказал, что для всех п существует абсолютная постоянная C₁ такой, что

${ displaystyle sup _ {x in mathbb {R}} left | F_ {n} (x) - Phi (x) right | leq C_ {1} cdot psi _ {1}, (2)}$

куда

${ displaystyle psi _ {1} = psi _ {1} { big (} { vec { sigma}}, { vec { rho}} { big)} = { Big (} { textstyle sum limits _ {i = 1} ^ {n} sigma _ {i} ^ {2}} { Big)} ^ {- 1/2} cdot max _ {1 leq i leq n} { frac { rho _ {i}} { sigma _ {i} ^ {2}}}.}$

Самостоятельно в 1942 г. Карл-Густав Эссеен доказал, что для всех п существует абсолютная постоянная C₀ такой, что

${ displaystyle sup _ {x in mathbb {R}} left | F_ {n} (x) - Phi (x) right | leq C_ {0} cdot psi _ {0}, (3)}$

куда

${ displaystyle psi _ {0} = psi _ {0} { big (} { vec { sigma}}, { vec { rho}} { big)} = { Big (} { textstyle sum limits _ {i = 1} ^ {n} sigma _ {i} ^ {2}} { Big)} ^ {- 3/2} cdot sum limits _ {i = 1 } ^ {n} rho _ {i}.}$

Легко убедиться, что ψ₀≤ψ₁. В связи с этим неравенство (3) принято называть неравенством Берри – Эссеена, а величина ψ₀ называется дробью Ляпунова третьего порядка. Более того, в случае, когда слагаемые Икс₁, ..., Икс_п иметь идентичные распределения

${ displaystyle psi _ {0} = psi _ {1} = { frac { rho _ {1}} { sigma _ {1} ^ {3} { sqrt {n}}}},}$

и, таким образом, оценки, установленные неравенствами (1), (2) и (3), совпадают без учета константы.

Касательно C₀, очевидно, нижняя оценка, установленная Эссеен (1956) остается в силе:

${ displaystyle C_ {0} geq { frac {{ sqrt {10}} + 3} {6 { sqrt {2 pi}}}} = 0,4097 ldots.}$

Верхние оценки для C₀ были впоследствии снижены с первоначальной оценки 7,59 из-за Эссеен (1942) до (учитывая только последние результаты) 0,9051 из-за Золотарев (1967), 0,7975 за счет ван Бик (1972), 0,7915 за счет Шиганов (1986), 0,6379 и 0,5606 из-за Тюрин (2009) и Тюрин (2010). По состоянию на 2011 г.^{[Обновить]} лучшая оценка 0,5600, полученная Шевцова (2010).

Многомерная версия

Как и в случае с многомерная центральная предельная теорема, существует многомерная версия теоремы Берри – Эссеена.^[1][2]

Позволять ${ Displaystyle X_ {1}, точки, X_ {n}}$ быть независимым ${ Displaystyle mathbb {R} ^ {d}}$-значные случайные векторы, каждый из которых имеет нулевое среднее значение. Написать ${ Displaystyle S = сумма _ {я = 1} ^ {п} X_ {я}}$ и предполагать ${ Displaystyle Sigma = OperatorName {Cov} [S]}$ обратимо. Позволять ${ Displaystyle Z sim OperatorName {N} (0, Sigma)}$ быть ${ displaystyle d}$-мерный гауссовский с тем же средним и ковариационной матрицей, что и ${ displaystyle S}$. Тогда для всех выпуклых множеств ${ Displaystyle U substeq mathbb {R} ^ {d}}$,

${ displaystyle { big |} Pr [S in U] - Pr [Z in U] , { big |} leq Cd ^ {1/4} gamma}$,

куда ${ displaystyle C}$ - универсальная постоянная и ${ displaystyle gamma = sum _ {i = 1} ^ {n} operatorname {E} { big [} | Sigma ^ {- 1/2} X_ {i} | _ {2} ^ {3} { big]}}$ (третья степень L² норма ).

Зависимость от ${ displaystyle d ^ {1/4}}$ предполагается оптимальным, но, возможно, в этом нет необходимости.

Смотрите также

• Неравенство Чернова
• Серия Эджворта
• Список неравенств
• Список математических теорем
• Неравенство концентраций

Примечания

Рекомендации

внешняя ссылка

• Гут, Аллан и Холст Ларс. Карл-Густав Эссеен, получено 15 марта 2004 г.
• «Неравенство Берри – Эссеена», Энциклопедия математики, EMS Press, 2001 [1994]